Work Energy Problem - Sliding Down a Ramp
TLDRIn this educational video, Physics Ninja tackles a work-energy theorem problem involving a block sliding down a ramp and then onto a flat section with varying coefficients of friction. The block starts from rest at the top of a 5m high ramp inclined at 20 degrees. The challenge is to find the distance 'D' the block slides on the flat section before its speed reduces to 0.15 m/s. The video demonstrates the application of the work-energy theorem, force analysis, and trigonometry to solve for 'D', emphasizing the importance of understanding work done by different forces and the cancellation of terms due to perpendicular displacements.
Takeaways
- 📚 The video is a physics lesson focused on the work-energy theorem.
- 🔍 The problem involves a block sliding down a ramp and then onto a flat section with different coefficients of friction.
- 📏 The block starts from rest at the top of a 5m high ramp inclined at 20 degrees.
- 🚫 The initial velocity of the block is zero, and the mass is not given but will cancel out in the calculations.
- 📐 The work-energy theorem is applied to find the distance 'D' the block slides on the flat section after leaving the ramp.
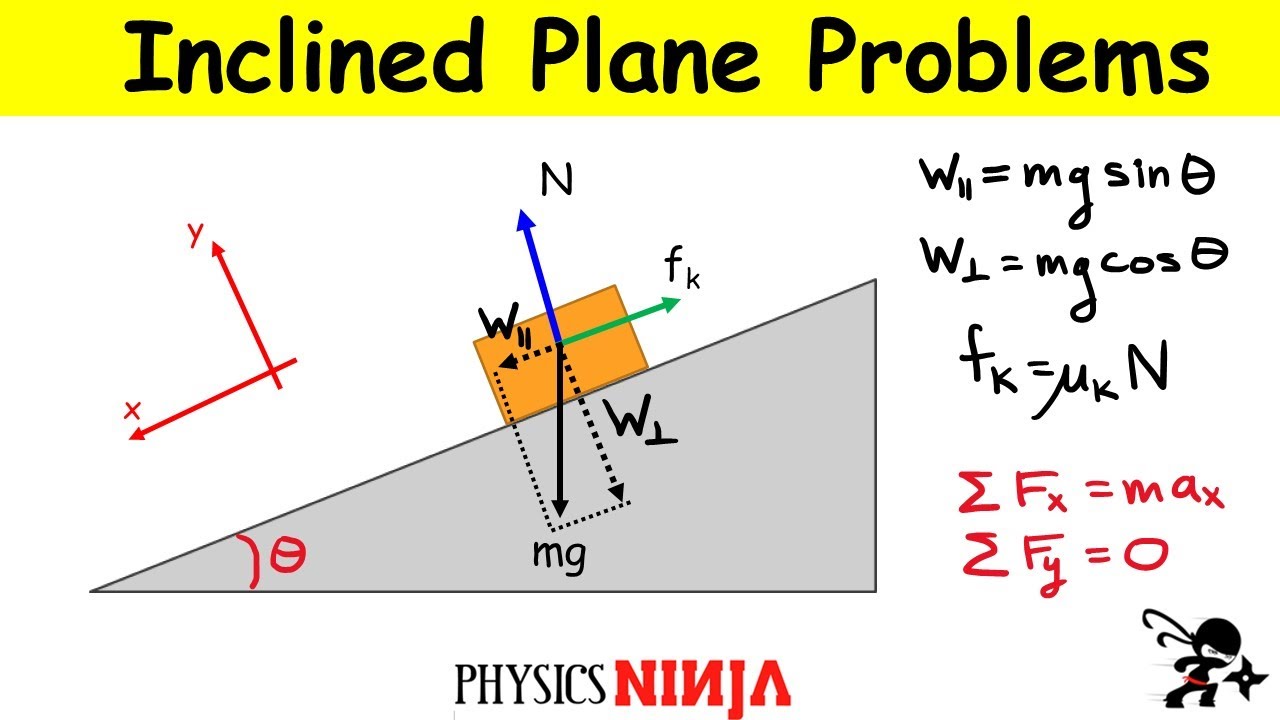
- 🔧 The forces acting on the block include gravity, normal force, and friction, with different coefficients for the ramp and flat section.
- 📉 The normal force does not do work as it is perpendicular to the displacement on both the ramp and the flat section.
- ⚖️ Work done by gravity and friction are the only forces considered in the calculations, as they are parallel to the displacement.
- 📘 The work done by gravity is calculated by breaking the weight into components and considering the parallel component to the ramp.
- 📌 The distance 'D1' the block slides down the ramp is found using trigonometry, relating the height and angle of the ramp.
- 🔢 The final calculation involves substituting known values into an equation derived from the work-energy theorem to solve for 'D'.
- 🧮 The final result of the distance 'D' is found to be 14.5 meters, which is similar to the ramp's length, depending on the given coefficients and angles.
Q & A
What is the main topic of the video?
-The main topic of the video is a physics problem involving the work-energy theorem, specifically calculating the distance a block slides on a flat section after descending a ramp.
What are the initial conditions of the block in the problem?
-The block starts at the top of a ramp with an initial velocity of zero and a height of 5 meters above the flat section.
What is the angle of the ramp with the horizontal?
-The angle of the ramp with the horizontal is 20 degrees.
What is the final velocity of the block after sliding the certain distance on the flat section?
-The final velocity of the block on the flat section is given as 0.15 m/s.
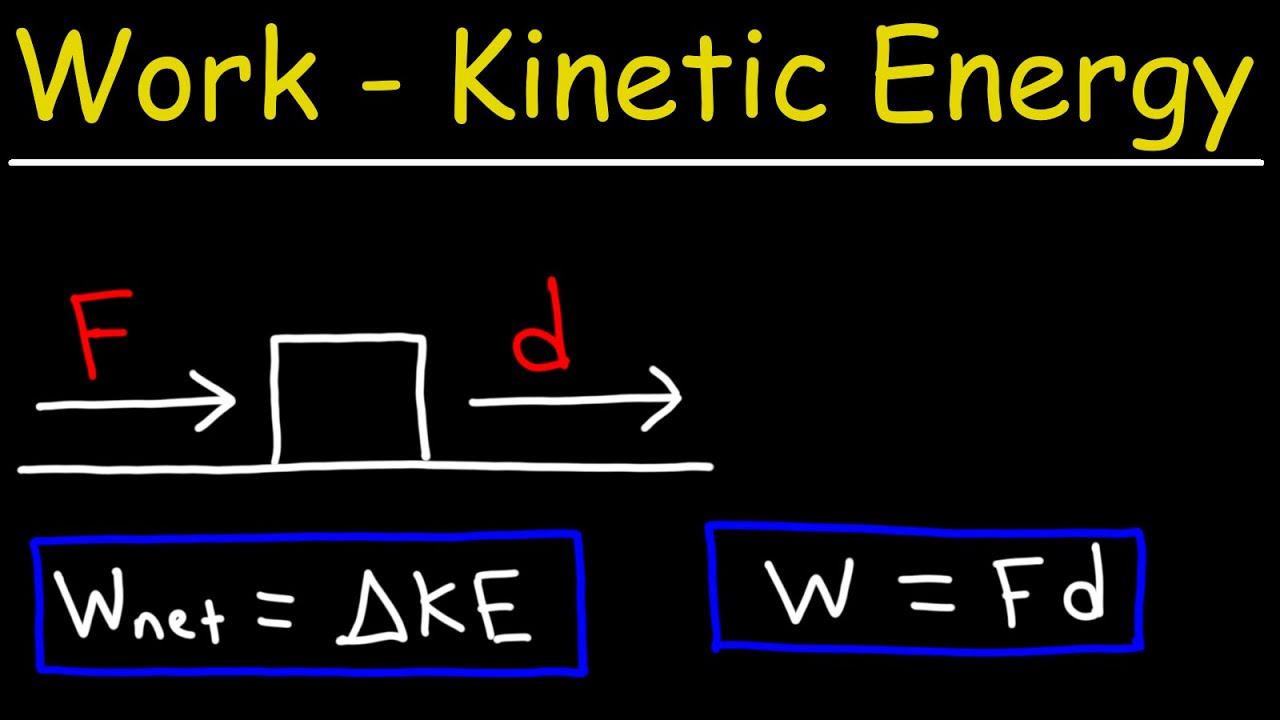
What is the work-energy theorem mentioned in the video?
-The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy.
Why does the mass of the block cancel out in the calculations?
-The mass cancels out because it appears in both the initial and final kinetic energy terms, and since the initial kinetic energy is zero (the block starts from rest), the mass terms cancel when setting the net work equal to the change in kinetic energy.
What forces act on the block as it slides down the ramp?
-The forces acting on the block as it slides down the ramp include gravity (mg acting downward), the normal force (perpendicular to the ramp surface), and the force of friction (opposite to the direction of motion).
Why doesn't the normal force do any work on the block?
-The normal force does not do any work because it is always perpendicular to the displacement of the block, whether on the ramp or the flat section.
How is the work done by gravity calculated on the ramp?
-The work done by gravity on the ramp is calculated by considering the component of the gravitational force parallel to the ramp (mg sin(theta)) and multiplying it by the distance slid down the ramp (D1).
What is the relationship between the coefficient of kinetic friction and the distance D the block slides on the flat section?
-The relationship is that a smaller coefficient of kinetic friction (mu2) results in a larger distance D the block will slide on the flat section, assuming other factors remain constant.
What was the final result for the distance D after substituting all the given values?
-The final result for the distance D, after substituting all the given values into the derived equation, was 14.5 meters.
Outlines
📚 Introduction to the Work-Energy Theorem Problem
In this paragraph, Physics Ninja introduces a problem involving the work-energy theorem. The scenario describes a block starting from rest at the top of a 5-meter high ramp inclined at 20 degrees. The block slides down the ramp, where the coefficient of friction differs from that on the flat section of the road. The goal is to find the distance 'D' the block slides on the flat section before coming to a speed of 0.15 m/s. The video encourages viewers to attempt the problem before revealing the solution, emphasizing the importance of understanding the work-energy theorem, identifying forces, and calculating work done by these forces.
🔍 Analyzing Forces and Work Done on the Ramp and Flat Section
This paragraph delves into the forces acting on the block: gravity, normal force, and friction. It explains that the normal force does no work since it's perpendicular to displacement. The focus then shifts to calculating the work done by gravity and friction on the ramp, using trigonometry to find the ramp's length 'D1' and breaking down the weight into components. The work done by friction is considered, with the force of kinetic friction on the ramp being the product of the coefficient of friction (μ1) and the normal force. The normal force on the flat section (N2) is identified as mg, and the work done by friction on the flat section is also calculated, leading to an equation that relates these forces to the block's final kinetic energy.
🧠 Solving for the Sliding Distance 'D' Using Work-Energy Theorem
The final paragraph presents the process of solving for the unknown distance 'D'. It involves simplifying the work-energy equation by eliminating the mass 'm' and rearranging terms to isolate 'D'. The paragraph explains how to calculate 'D1' using the height and angle of the ramp, and then substitutes known values into the equation, including the height, angle, coefficients of friction (μ1 and μ2), and the final velocity. The solution process involves careful algebraic manipulation to express 'D' in terms of the given parameters. The final result of 14.5 meters for 'D' is obtained by substituting the values into the derived equation, highlighting the sensitivity of 'D' to the height of the ramp and the coefficients of friction.
Mindmap
Keywords
💡Work Energy Theorem
💡Ramp
💡Initial Velocity
💡Angle
💡Coefficient of Friction
💡Flat Section
💡Kinetic Energy
💡Displacement
💡Normal Force
💡Trigonometry
💡Free Body Diagram
Highlights
Introduction to a work-energy theorem problem involving a block sliding down a ramp and onto a flat section with different coefficients of friction.
The block starts from rest at the top of a ramp with a height of 5 meters.
The ramp makes an angle of 20 degrees with the horizontal.
The coefficient of friction is different on the ramp and the flat section.
The block's final velocity on the flat section is given as 0.15 m/s.
The work-energy theorem is used to solve for the unknown distance D on the flat section.
The initial kinetic energy is zero as the block starts from rest.
The forces acting on the block on the ramp include weight, normal force, and friction.
On the flat section, the forces include weight, normal force, and a different coefficient of friction.
The normal force does no work as it is always perpendicular to the displacement.
The work done by gravity on the ramp is calculated using the component of weight parallel to the ramp.
The work done by friction on the ramp is calculated using the force of kinetic friction and the displacement.
The work done by friction on the flat section is calculated similarly, with a different coefficient.
The expression for the work done includes terms that simplify when mass is canceled out.
The distance D1 down the ramp is calculated using trigonometry, relating height and angle.
The final expression for D involves substituting known values and solving for the unknown distance.
The final result for the distance D is found to be 14.5 meters, similar to the ramp's distance.
The importance of understanding the differences in work done on the ramp and the flat section is emphasized.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: