Conservative & Nonconservative Forces, Kinetic & Potential Energy, Mechanical Energy Conservation
TLDRThis educational script explores the distinction between conservative and non-conservative forces, using gravity and friction as examples. It elucidates that the work done by conservative forces is path-independent, while non-conservative forces' work is path-dependent. The script then delves into the implications of these forces on mechanical energy, highlighting the conservation of mechanical energy in systems with only conservative forces at play. It concludes with a practical example of a falling ball to illustrate the principle of conservation of mechanical energy.
Takeaways
- 🔍 The difference between conservative and non-conservative forces lies in the dependency of work done on the path taken; conservative forces are path-independent, while non-conservative forces are path-dependent.
- 🌐 Examples of conservative forces include the electric force between charges and gravity, whereas friction and applied forces like pushing or pulling are non-conservative forces.
- 📐 The work done by a conservative force is the same regardless of the path taken between two points, as long as the height difference remains constant.
- 🔄 The work done by a non-conservative force, such as friction, varies with the path taken due to factors like distance traveled.
- ⚙️ The net work done on an object is the sum of the work done by all forces, including both conservative and non-conservative forces.
- 🌡 The work done by all conservative forces is equal to the negative change in potential energy of the object.
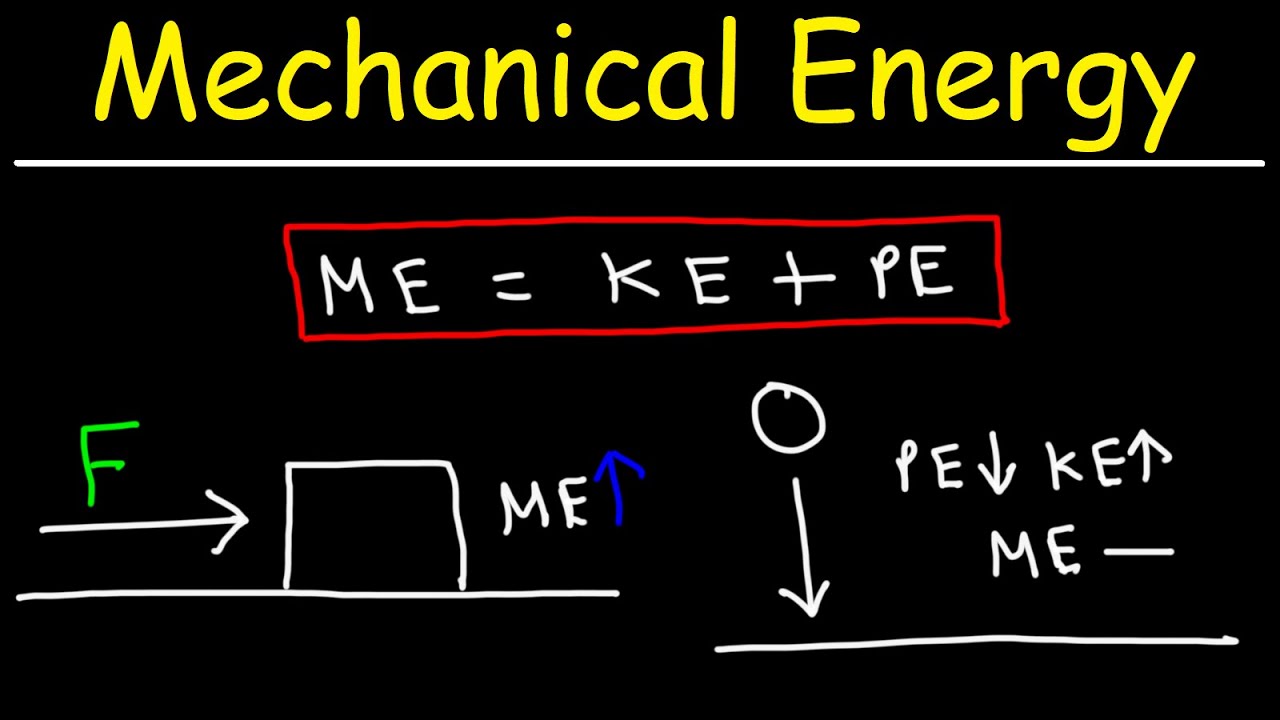
- 🚀 The work done by all non-conservative forces is equal to the change in the mechanical energy of the object, which is the sum of kinetic and potential energy.
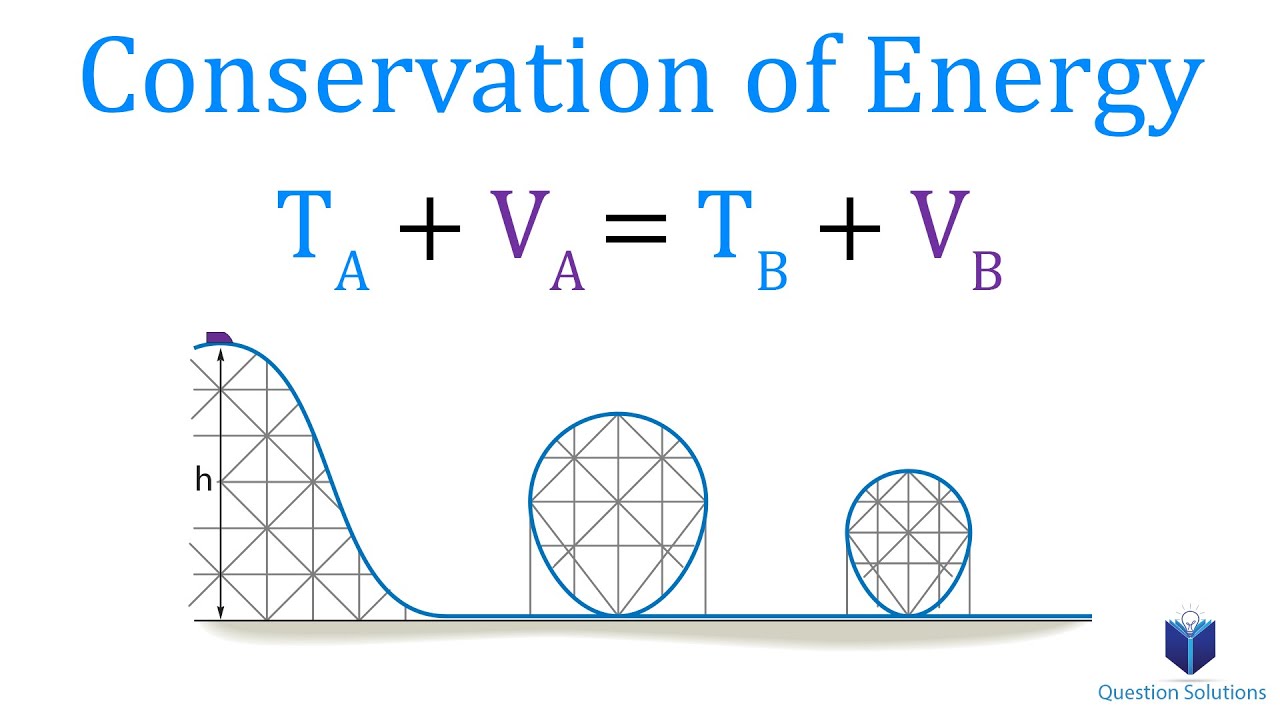
- 🔄 The principle of conservation of mechanical energy states that in a system with only conservative forces, the total mechanical energy remains constant, as the work done by non-conservative forces is zero.
- 📉 In the absence of non-conservative forces, the change in mechanical energy is zero, illustrating the conservation of energy in such a system.
- 📚 Three key formulas to remember are: the change in kinetic energy equals the net work done on an object, the work done by conservative forces equals the negative change in potential energy, and the work done by non-conservative forces equals the change in mechanical energy.
- 📉 An example calculation demonstrates that the mechanical energy is conserved when only gravity (a conservative force) acts on a falling object, as the sum of kinetic and potential energy remains constant throughout the fall.
Q & A
What is the main difference between a conservative force and a non-conservative force?
-The main difference lies in how the work done by these forces depends on the path taken. Work done by a conservative force is path-independent, meaning it does not depend on the path taken between two points. In contrast, work done by a non-conservative force is path-dependent and varies with the path taken.
Can you provide an example of a conservative force?
-An example of a conservative force is the electric force between charges, or gravity. The work done by these forces does not depend on the path taken between two points.
What is an example of a non-conservative force?
-Friction is an example of a non-conservative force. The work done by friction depends on the path taken, and it generally decreases the kinetic energy of an object.
How does the work done by gravity relate to the path taken?
-The work done by gravity is independent of the path taken. This means that the work done by gravity to move an object from one point to another is the same regardless of whether the path is direct or curved, as long as the height difference remains the same.
Why does the work done by friction differ between different paths?
-The work done by friction differs because friction is a non-conservative force that depends on the path taken. A longer path, such as a curved path, will result in more work being done by friction, leading to a greater decrease in kinetic energy.
What is the relationship between the work done by all forces on an object and the change in kinetic energy?
-The net work done on an object is equal to the change in its kinetic energy. This principle is fundamental in understanding how forces affect the motion of an object.
How is the work done by conservative forces related to potential energy?
-The work done by all conservative forces is equal to the negative change in potential energy of the object. This relationship is crucial in understanding the conservation of mechanical energy in a system.
What is the principle of conservation of mechanical energy?
-The principle of conservation of mechanical energy states that in a system where only conservative forces are acting, the total mechanical energy (the sum of kinetic and potential energy) remains constant. This means there is no net change in mechanical energy.
How can you calculate the final speed of a ball falling from a height?
-You can calculate the final speed using the kinematic equation \( v_{\text{final}}^2 = v_{\text{initial}}^2 + 2a\Delta y \), where \( v_{\text{initial}} \) is the initial speed, \( a \) is the acceleration due to gravity, and \( \Delta y \) is the displacement in the direction of gravity.
Why is mechanical energy conserved in a system with only conservative forces?
-Mechanical energy is conserved in such a system because the work done by non-conservative forces is zero. Since there are no non-conservative forces acting, the total mechanical energy (kinetic plus potential energy) does not change.
What is the formula for calculating gravitational potential energy?
-The gravitational potential energy (PE) is calculated using the formula \( PE = mgh \), where \( m \) is the mass of the object, \( g \) is the acceleration due to gravity, and \( h \) is the height above a reference point.
Outlines
🔍 Understanding Conservative and Non-Conservative Forces
This paragraph introduces the concept of conservative and non-conservative forces. Conservative forces, such as the electric force between charges and gravity, do not depend on the path taken when doing work. In contrast, non-conservative forces, like friction and any applied push or pull, do depend on the path. The paragraph uses the example of gravity and friction to illustrate how the work done by these forces is path-independent or path-dependent, respectively. It also explains the difference between the two by showing that the work done by gravity remains constant regardless of the path taken, while the work done by friction varies with the length and nature of the path.
📚 Formulas and Principles of Work and Energy
The second paragraph delves into the relationship between work, energy, and the types of forces acting on an object. It explains that the net work done on an object is equal to the change in its kinetic energy, while the work done by conservative forces equates to the negative change in potential energy. The paragraph introduces the formula for non-conservative forces, which is the difference between the net work and the work done by conservative forces, and relates this to the change in mechanical energy. It concludes with the principle of conservation of mechanical energy, stating that in a system with only conservative forces, the mechanical energy remains constant, as there is no work done by non-conservative forces.
📉 Conservation of Mechanical Energy: An Illustrative Example
The final paragraph provides an example to demonstrate the principle of conservation of mechanical energy. It describes a scenario where a ball falls from a height of 100 meters to 30 meters above the ground, calculating the final speed and kinetic energy at the lower position. The paragraph also calculates the potential energy at both positions and shows that the total mechanical energy (sum of kinetic and potential energy) remains constant throughout the fall. This example reinforces the concept that in the absence of non-conservative forces, the mechanical energy of a system is conserved.
Mindmap
Keywords
💡Conservative Force
💡Non-conservative Force
💡Work
💡Potential Energy
💡Kinetic Energy
💡Mechanical Energy
💡Path Independence
💡Path Dependence
💡Friction
💡Applied Force
💡Conservation of Mechanical Energy
Highlights
The difference between conservative and non-conservative forces is that work done by a conservative force is path-independent, while a non-conservative force's work is path-dependent.
Examples of conservative forces include the electric force between charges and the elastic force in a spring.
Friction and any applied force, such as pushing or pulling, are non-conservative forces.
Conservative forces, like gravity, perform the same amount of work regardless of the path taken between two points.
Non-conservative forces, such as friction, perform different amounts of work depending on the path taken.
The work-energy theorem relates the net work done on an object to the change in its kinetic energy.
The work done by conservative forces is equal to the negative change in potential energy.
Potential energy can only be defined for conservative forces.
The work done by non-conservative forces equals the change in mechanical energy of an object.
Mechanical energy is the sum of kinetic and potential energy of an object.
In a system with only conservative forces, the mechanical energy remains constant, illustrating the principle of conservation of mechanical energy.
The conservation of mechanical energy principle states that in a system with only conservative forces, the total mechanical energy does not change.
An example of calculating the final speed of a falling ball demonstrates the conservation of mechanical energy.
The mechanical energy of a falling ball remains constant when only gravity acts on it, with no friction or air resistance.
The formulas for the change in kinetic energy, work done by conservative forces, and work done by non-conservative forces are essential for understanding energy conservation.
The conservation of mechanical energy principle is fundamental in physics for analyzing systems with only conservative forces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: