Exponential Growth and Decay BC Calc

Chad Gilliland
14 Jan 201313:35
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video explores exponential growth and decay, focusing on solving differential equations where the rate of change is proportional to the current amount. It covers key concepts like half-life, continuous compounding, and provides formulas for calculating growth rates and decay rates, using examples from population dynamics, radioactive decay, and compound interest.

Takeaways
  • 📚 The video discusses exponential growth and decay, focusing on solving problems where the rate of growth is proportional to the amount present.
  • 🔍 The script introduces the differential equation \( \frac{dy}{dt} = k \cdot y \), which is fundamental in modeling exponential growth and decay.
  • 🧩 The general solution to the differential equation is \( y = Ce^{kt} \), where \( C \) is the initial condition, \( k \) is the constant of proportionality, and \( t \) is time.
  • 🌱 In the context of population growth, the rate of growth increases with the number of individuals, illustrating how more people lead to faster population growth.
  • 💰 Similarly, in financial contexts, more money in a savings account leads to faster growth due to compound interest.
  • ⏳ The script explains how to use the formula \( y = Ce^{kt} \) to solve for exponential growth or decay, emphasizing its versatility.
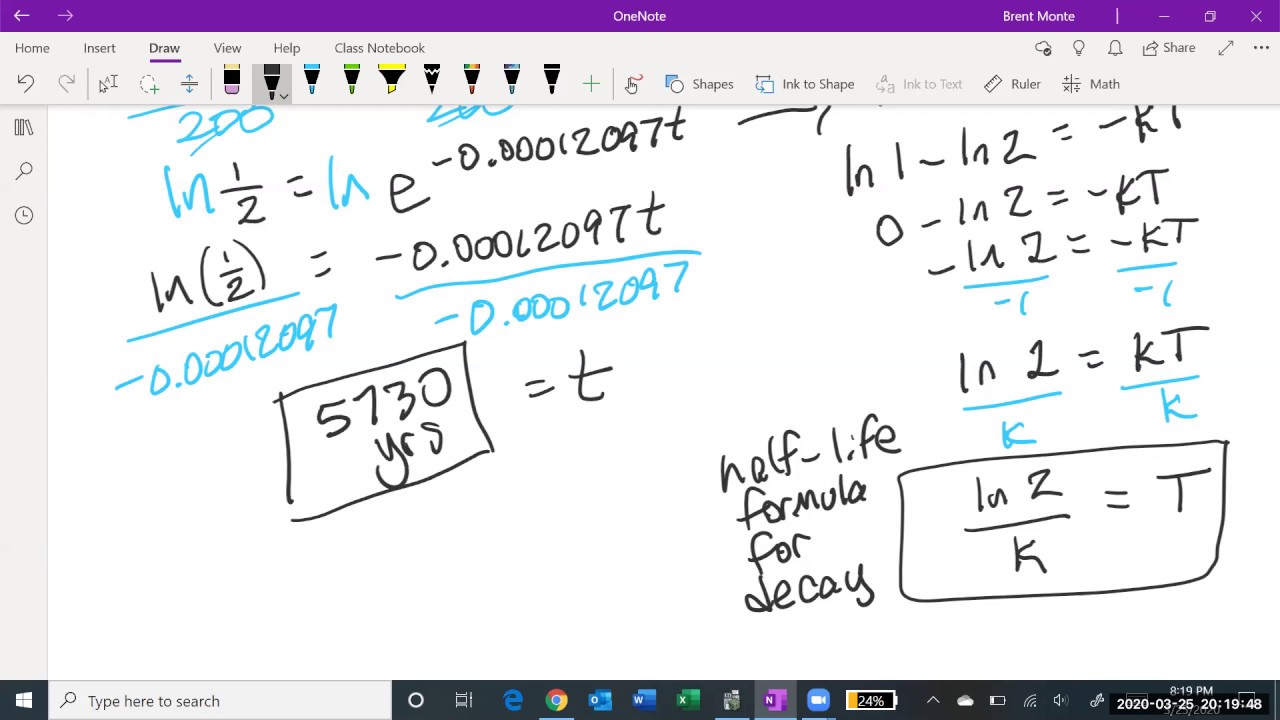
  • 📉 The concept of half-life is introduced, showing how it can be used to determine the decay rate \( k \) in radioactive decay problems.
  • 📈 An example is given where the balance in an account triples in 13 years, demonstrating how to calculate the annual percentage rate using continuous compounding.
  • 📊 The script provides a method to estimate future population sizes using the exponential decay model, showing its application in demographic studies.
  • 🔢 The importance of understanding the initial condition \( C \), the growth or decay rate \( k \), and the time \( t \) is emphasized for solving exponential growth and decay problems.
  • 🔄 The video concludes with a summary of the key concepts, reinforcing the formula \( y = Ce^{kt} \) as a tool for solving a wide range of exponential growth and decay problems.
Q & A

  • What is the main topic discussed in the video?

    -The main topic discussed in the video is exponential growth and decay, specifically focusing on solving problems related to situations where the rate of growth is proportional to the amount present, using the K formula.

  • What does the differential equation dy/dt = k*y represent?

    -The differential equation dy/dt = k*y represents a situation where the rate of change (dy/dt) is proportional to the current amount (y), with k being the constant of proportionality. This is commonly seen in exponential growth and decay problems.

  • What is the general formula for exponential growth or decay?

    -The general formula for exponential growth or decay is y = C * e^(kt), where y is the amount present, C is the initial condition, k is the growth or decay rate, and t is time.

  • What is the significance of the constant k in the exponential growth or decay formula?

    -The constant k in the exponential growth or decay formula represents the rate of growth or decay. A positive k indicates growth, while a negative k indicates decay.

  • How does the initial condition C relate to the formula y = C * e^(kt)?

    -The initial condition C is the starting amount present at time t=0. It is a crucial part of the formula, as it sets the base level from which exponential growth or decay occurs.

  • What is a half-life, and how does it relate to exponential decay?

    -A half-life is the time it takes for a substance to decay to half of its initial amount. In the context of exponential decay, the half-life is used to determine the decay rate constant k.

  • How can you find the decay rate constant k for a radioactive substance with a half-life of 30 days?

    -To find the decay rate constant k for a radioactive substance with a half-life of 30 days, you can use the formula e^(-k*t) = 1/2, where t is the half-life. Solving for k gives k = ln(1/2) / t.

  • What is the formula for continuous compound interest, and how does it relate to exponential growth?

    -The formula for continuous compound interest is A = P * e^(rt), where A is the amount of money accumulated after n years, including interest, P is the principal amount, r is the annual interest rate, and t is the time the money is invested or borrowed for. This is a specific case of exponential growth where the principal is compounded continuously.

  • How can you calculate the annual percentage rate (APR) for an account that triples in 13 years with continuous compounding?

    -To calculate the APR for an account that triples in 13 years with continuous compounding, you can use the formula e^(13k) = 3, where k is the growth rate. Solving for k gives k = ln(3) / 13, and then multiplying by 100 gives the APR as a percentage.

  • What is the process for estimating the population in the year 2020 for a population that decreased continuously from 21,000 to 20,000 between 1990 and 2000?

    -To estimate the population in the year 2020, you first find the decay rate constant k using the formula ln(20/21) = 10k. Then, use the formula y = 21,000 * e^(kt) with t=30 to calculate the population for the year 2020.

  • How can you determine the number of bacteria present five hours after an initial count of 500, if the population doubles every two hours?

    -To determine the number of bacteria present five hours after an initial count of 500, you use the formula y = 500 * e^(k*t), where k is the growth rate constant found by solving ln(2) = 2k. Then, plug in t=5 to find the population at that time.

Outlines
00:00
📚 Introduction to Exponential Growth and Decay

The script begins by introducing the concept of exponential growth and decay, focusing on how the rate of growth is proportional to the amount present. It explains that this principle applies to various scenarios such as population growth, financial interest, and radioactive decay. The presenter aims to solve the differential equation that represents this relationship, leading to a general formula for exponential growth or decay. The formula derived is \( y = Ce^{KT} \), where \( C \) is the initial amount, \( K \) is the rate of growth or decay, \( T \) is time, and \( e \) is the base of the natural logarithm. The summary also clarifies the meaning of each variable in the context of different examples, such as population growth and radioactive decay.

05:00
🔍 Calculating Decay Rates and Compound Interest

This paragraph delves into specific examples to illustrate the application of the exponential growth and decay formula. It starts with calculating the decay rate of a radioactive substance with a half-life of 30 days, using the initial condition and the concept of half-life to determine the decay constant \( K \). The presenter then moves on to an example of continuous compound interest, where an account balance triples in 13 years, and uses the formula to find the annual percentage rate. The summary emphasizes the process of solving for \( K \) in different scenarios, whether it involves decay or growth, and how to apply the formula to find unknown variables.

10:02
📉 Analyzing Population Decline and Bacterial Growth

The final paragraph presents two more examples: a declining population and the growth of bacteria. For the population, which decreased from 21,000 to 20,000 between 1990 and 2000, the script calculates the decay rate and uses it to predict the population for the year 2020. The bacteria example shows how to use the exponential growth formula when the quantity doubles in a given time frame, calculating the growth rate and predicting the number of bacteria five hours from the initial time. The summary highlights the process of deriving the decay or growth rate from given data and applying it to forecast future values using the exponential formula.

Mindmap
Keywords
💡Exponential Growth
Exponential growth refers to a process where a quantity increases at a rate proportional to its current value. In the video, it is the central theme, illustrating how certain phenomena, such as population growth or financial investments, expand rapidly over time. The script uses the formula 'dy/dt = k*y' to describe this growth, where 'k' is the growth rate and 'y' is the current amount.
💡Differential Equation
A differential equation is an equation that relates a function with its derivatives, which is used to describe rates of change. In the context of the video, the differential equation 'dy/dt = k*y' is solved to understand exponential growth. The script demonstrates the separation of variables and integration to solve for 'y', resulting in the exponential growth formula.
💡Separation of Variables
Separation of variables is a method used to solve differential equations by rearranging the equation so that all terms involving one variable are on one side and the other variable on the opposite side. The script describes this process when solving the exponential growth differential equation, moving 'y' terms to one side and 'dt' terms to the other, facilitating integration.
💡Integral
An integral is a mathematical concept that represents the area under a curve, used in calculus to find the accumulated change of a quantity. In the video, integration is used to find the solution to the differential equation, leading to the natural logarithm of 'y' being equal to 'k*t' plus a constant.
💡Natural Logarithm
The natural logarithm, often denoted as 'ln', is the logarithm to the base 'e', where 'e' is an irrational constant approximately equal to 2.71828. In the video, the natural logarithm is used to simplify the equation after integration, resulting in 'ln(y) = k*t + C', where 'C' is the constant of integration.
💡Exponential Decay
Exponential decay is the opposite of exponential growth, where a quantity decreases at a rate proportional to its current value. The script discusses this in the context of half-life, where substances like radioactive materials decrease in quantity over time according to an exponential function.
💡Half-Life
Half-life is the time required for half of a substance to decay or be removed. In the script, the concept is used to calculate the decay rate 'k' for a radioactive substance with a 30-day half-life, demonstrating how to use the exponential decay formula to find the remaining amount after a certain time.
💡Continuous Compound Interest
Continuous compound interest is a method of calculating interest where the interest is added to the principal continually, rather than at discrete intervals. The script uses this concept to explain how an account balance can triple in 13 years when interest is compounded continuously, deriving the annual percentage rate using the exponential growth formula.
💡Initial Condition
An initial condition is a value assigned to a variable at the beginning of a process. In the video, the initial condition is used to determine the constant 'C' in the exponential growth formula. For example, if a population starts with 10,000 individuals, this number is the initial condition for that population growth model.
💡Growth Rate
The growth rate is the speed at which a quantity increases over time. In the context of the video, 'k' represents the growth rate in the exponential growth formula. If 'k' is positive, it indicates growth, while a negative 'k' would indicate decay. The script provides examples of calculating 'k' for different scenarios, such as population growth and financial investments.
💡Population Dynamics
Population dynamics refers to the study of how the size and age composition of a population change over time. The script touches on this concept when discussing how a population can grow or decay exponentially, using the exponential growth formula to model changes in population size from year to year.
Highlights

Introduction to exponential growth and decay in K formulas.

Explanation of the differential equation for exponential growth or decay.

Separation of variables to solve the differential equation.

Integration to find the natural logarithm relationship.

Conversion of the natural logarithm to an exponential form.

General formula for exponential growth and decay.

Use of the initial condition to determine the constant C.

Interpretation of K as the growth or decay rate.

Application to population growth and money in savings accounts.

Example of writing the equation for a radioactive substance with a half-life.

Method to determine the decay rate using half-life.

Calculation of the annual percentage rate for continuous compounding.

Use of the natural logarithm to solve for the growth rate in a decay situation.

Estimation of population decline using the exponential decay formula.

Example of bacterial growth using the exponential growth formula.

Determination of the growth rate and prediction of future population using the formula.

Summary of the practical applications of exponential growth and decay formulas.

Transcripts

Browse More Related Video

What is e and ln(x)? (Euler's Constant and The Natural Logarithm)

Exponential Growth and Decay (Precalculus - College Algebra 66)

Math 11 - Section 2.5 (previously section 3.4)

AP Calculus AB - 7.8 Exponential Models With Differential Equations

Calculus AB/BC – 7.8 Exponential Models with Differential Equations

Applications with Separable Equations (Differential Equations 14)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Exponential GrowthDecay RatesContinuous CompoundingDifferential EquationsHalf-LifePopulation DynamicsRadioactive DecayInterest RatesEconomic ModelsEducational Content