Intermediate Value Theorem

Chad Gilliland
27 Aug 201307:37
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, the instructor introduces the Intermediate Value Theorem, an important concept in calculus that proves the existence of certain values within a continuous function. Using examples such as a person's height over time, the instructor explains how any value between two points must be reached if the function is continuous. The lesson emphasizes the importance of continuity and guides viewers through graphical examples, checking for continuity issues, and determining where the function intersects specific values. The session concludes with a polynomial example for students to solve independently.

Takeaways
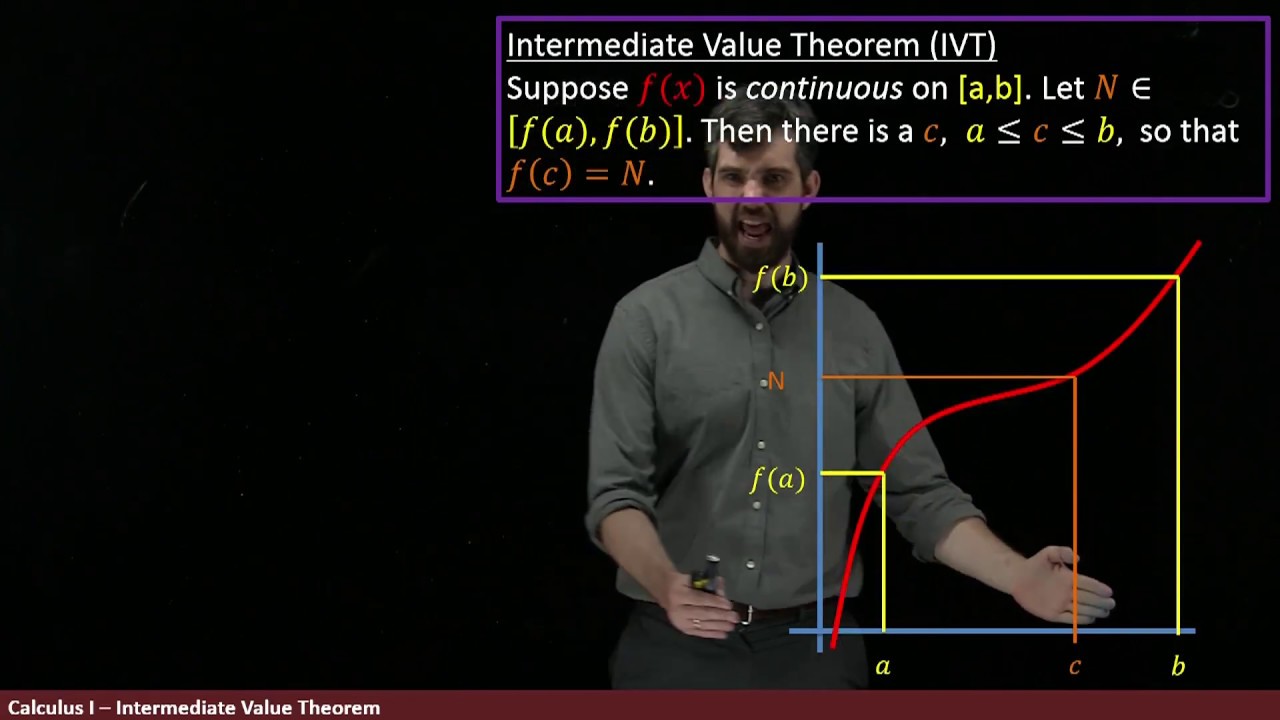
  • 📚 The Intermediate Value Theorem (IVT) is a fundamental theorem in calculus that proves the existence of a value within a continuous function.
  • 🔍 The IVT is used to establish that a continuous function takes on every value between two given y-values within its domain.
  • 📈 An example given is a person's height as a continuous function of age, illustrating that if one's height is 58 inches at age 11 and 64 inches at age 14, they must have been every height in between at some point during those years.
  • 📝 The theorem requires the function to be continuous, meaning no gaps or holes in the graph, which is a prerequisite for the IVT to apply.
  • 🚫 The y-values at the endpoints of the interval (f(a) and f(b)) must not be equal; they should be distinct for the theorem to hold true.
  • 📉 The IVT does not state that the function cannot exceed f(b) or go below f(a); it only guarantees that all y-values between f(a) and f(b) are taken at least once.
  • 🔍 To apply the IVT, one must check for continuity within the interval of interest, avoiding points where the function may be discontinuous.
  • 📌 The theorem helps in determining where a graph crosses a horizontal line y=K, where K is between f(a) and f(b), by ensuring the existence of at least one point where the function equals K.
  • 📘 The script provides a method to check for continuity, such as avoiding division by zero or the presence of asymptotes, which would indicate discontinuity.
  • 📊 Two examples are given to demonstrate the application of the IVT: one with a function 1/(x-2) and another with a polynomial function, both illustrating how to find where the function crosses a specific y-value.
  • 📝 The script concludes with a challenge for the audience to apply the IVT to a polynomial function to find where it crosses the horizontal line y=4, encouraging active learning and problem-solving.
Q & A

  • What is the Intermediate Value Theorem?

    -The Intermediate Value Theorem (IVT) states that for any continuous function f(x) on the interval [a, b], if k is a value between f(a) and f(b), then there exists at least one value c in the interval [a, b] such that f(c) = k.

  • Why is the Intermediate Value Theorem important?

    -The IVT is important because it guarantees the existence of at least one value within a certain interval where the function takes on a specific value, which is crucial for proving the existence of solutions to equations.

  • What is an example of the IVT involving a person's height?

    -If a person was 58 inches tall at age 11 and 64 inches tall at age 14, the IVT guarantees that at some point between ages 11 and 14, the person's height was exactly 61.5 inches, 58.9 inches, or any other height between 58 and 64 inches.

  • What is a necessary condition for the IVT to hold?

    -A necessary condition for the IVT to hold is that the function must be continuous on the interval [a, b].

  • Why can't the two y-values in the IVT be equal?

    -The two y-values (f(a) and f(b)) can't be equal because the theorem requires them to be separated to guarantee that the function takes on every value between f(a) and f(b).

  • How can we visually understand the IVT?

    -Visually, if you connect the points (a, f(a)) and (b, f(b)) with a continuous line, the IVT guarantees that the line will cross every horizontal line between f(a) and f(b) at least once.

  • What happens if the function is not continuous?

    -If the function is not continuous, the IVT does not apply, and we cannot guarantee that the function will take on every value between f(a) and f(b).

  • What does the example involving f(x) = 1/(x-2) illustrate?

    -The example illustrates how to check the continuity of a function and apply the IVT to determine if a specific value of k is between f(a) and f(b) and thus must be crossed by the graph.

  • How do we find the value of c in the IVT example with f(x) = 1/(x-2)?

    -To find the value of c, we set the function f(x) equal to k and solve for x. In the example, solving 1/(x-2) = 1/4 gives x = 6, meaning the function crosses the horizontal line y = 1/4 at x = 6.

  • What is special about polynomials in the context of the IVT?

    -Polynomials are continuous everywhere on the entire number line, so the IVT always applies to polynomials on any interval.

  • What is the challenge given to the students in the last example?

    -The challenge is to determine where the polynomial x^2 + 5x - 6 intersects or crosses the horizontal line y = 4, using the IVT to find the specific value of x.

Outlines
00:00
📏 Understanding the Intermediate Value Theorem (IVT)

The video begins with an introduction to the Intermediate Value Theorem (IVT) in calculus, explaining its importance in proving the existence of certain values within a continuous function. Using the example of a person's height between ages 11 and 14, it demonstrates that every height between 58 and 64 inches is reached. The function's continuity is crucial, and no jumps in value can occur. The video describes the necessary conditions for IVT, including the requirement for the function to be continuous and for the y-values to differ. The concept is visually represented with a graph, highlighting that every y-value between two points must be crossed at least once by the function.

05:01
🧮 Applying the IVT to a Continuous Function Example

The next part explores applying the IVT to specific functions and intervals, determining if the theorem holds for a given value of K. The function 1/(x-2) is evaluated between 2.5 and 7, ensuring continuity and checking the values at these points. By comparing these values, the video confirms that 1/4 is between them, thus the horizontal line y=1/4 must be crossed. This section involves detailed calculations and graphical representation to illustrate how the continuous function intersects the horizontal line, reinforcing the IVT's application.

🔍 Finding Intersection Points Using IVT

This paragraph continues with a deeper dive into finding the exact points where the function intersects a specific y-value, setting f(x) equal to 1/4 and solving for x. The function's behavior and its graphical representation are discussed, demonstrating that at x=6, the function crosses y=1/4. The segment concludes with a brief discussion on polynomials' continuity, emphasizing that they are continuous across the entire number line and can be analyzed using the IVT.

📊 Homework: Identifying Intersection Points in Polynomials

In the final segment, the video presents a polynomial example to be solved as homework, ensuring students understand that all polynomials are continuous. By evaluating the polynomial at specific points, students need to determine if a given y-value is crossed within an interval. The task involves finding where the polynomial intersects y=4. The teacher encourages students to solve this on their own and bring their findings to the next class, reinforcing the lesson and ensuring comprehension of the IVT and its practical applications.

Mindmap
Keywords
💡Intermediate Value Theorem
The Intermediate Value Theorem (IVT) states that for any continuous function on a closed interval [a, b], if a value K lies between f(a) and f(b), then there exists at least one value c in the interval [a, b] such that f(c) = K. This theorem guarantees the existence of certain values within the range of a continuous function. In the video, it's illustrated using the example of a person's height, showing that every height between 58 and 64 inches is taken on at some point between ages 11 and 14.
💡Continuous Function
A continuous function is one without any gaps, jumps, or holes in its graph. For the IVT to apply, the function must be continuous over the given interval. The video emphasizes that continuity is essential for the theorem, as it ensures that every value between f(a) and f(b) is achieved by the function. Examples include the person's height over time and polynomial functions, which are continuous over the entire number line.
💡Existence Theorem
An existence theorem, like the IVT, guarantees that a solution to a particular problem exists under certain conditions. The IVT is introduced as the first existence theorem in calculus, assuring that certain values are achieved by a continuous function. The video demonstrates this concept by showing how intermediate values are inevitably reached within a given interval.
💡Height Example
The height example in the video demonstrates the IVT by showing that a person growing from 58 inches at age 11 to 64 inches at age 14 must have been every height in between at some point. This real-world example helps illustrate the abstract concept of the theorem by making it relatable and concrete.
💡K Value
The K value in the context of the IVT is a specific value that lies between f(a) and f(b). The theorem states that there must be at least one point c in the interval [a, b] where f(c) = K. In the video, K is used to demonstrate how intermediate values are reached, such as the specific height between 58 and 64 inches or the y-value in other mathematical examples.
💡F(a) and F(b)
F(a) and F(b) are the function values at the endpoints of the interval [a, b]. For the IVT to hold, these values must not be equal and the function must be continuous between them. The video uses these terms to set up examples and illustrate how the function must cross every value between F(a) and F(b).
💡Polynomials
Polynomials are a class of mathematical functions that are continuous everywhere. The video uses polynomials as examples to demonstrate the IVT because their continuous nature makes them ideal candidates for the theorem. The continuity of polynomials ensures that all intermediate values are achieved within any interval.
💡Graphical Representation
Graphical representation involves illustrating mathematical concepts using graphs. In the video, graphs are used to visually demonstrate the IVT, showing how a continuous function must intersect every value between F(a) and F(b). This helps in understanding the theorem by providing a visual aid to the abstract concept.
💡Continuity Problems
Continuity problems refer to issues in a function that prevent it from being continuous, such as division by zero or asymptotes. The video discusses how to identify these problems and their impact on applying the IVT. For example, the function 1/(x-2) has a continuity problem at x=2, which is crucial for determining whether the IVT applies.
💡Interval
An interval in mathematics is a range of values, typically defined by two endpoints. The IVT applies to continuous functions over a closed interval [a, b]. The video repeatedly references intervals to show how the theorem ensures that every intermediate value is achieved within that range, using various mathematical and real-world examples.
Highlights

Introduction to the Intermediate Value Theorem (IVT), a fundamental theorem in calculus that proves the existence of values.

IVT's application in proving a person's height as a continuous function of time.

Explanation of how the IVT implies taking on every height between two ages.

Clarification on the requirement for a function to be continuous for IVT to apply.

Condition that the two y-values must not be equal for IVT to hold.

Graphical representation of IVT, demonstrating the necessity to touch every y-value between two points.

Method to find where the graph crosses a horizontal line y equals K.

IVT does not restrict the function from exceeding the y-values of the interval.

Verification of continuity by checking for division by zero or asymptotes.

Example using the function f(x) = 1/(x-2) to demonstrate IVT, including continuity check.

Calculation of f(x) values to determine if IVT holds for a given value of K.

Determination of where the function crosses the line y = 1/4 within a specified interval.

All polynomials are continuous everywhere, satisfying the continuity requirement for IVT.

Example of a polynomial function and its continuity, with a challenge to find where it crosses y = 4.

Assignment to students to find the x-value where a polynomial crosses y = 4, fostering engagement with the material.

Invitation for students to discuss their findings in the next class, promoting active learning.

Transcripts

Browse More Related Video

Were you ever exactly 3 feet tall? The Intermediate Value Theorem

Calculus AB/BC – 1.16 Intermediate Value Theorem

AP Calculus AB - 1.16 Working with the Intermediate Value Theorem

1.2 - Algebraic Limits and Continuity

AP Calculus Review Three Theorems You Must Know (EVT, IVT, MVT)

Continuity!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Intermediate Value TheoremCalculusContinuous FunctionsHeight GrowthGraphical AnalysisExistence ProofPolynomialsFunction ContinuityMathematics EducationTheorem Application