Worked example: interval of convergence | Series | AP Calculus BC | Khan Academy
TLDRThis instructional video explores the convergence of an infinite series using the ratio test. The instructor guides viewers to determine the interval of convergence by calculating the limit of the ratio of consecutive terms as n approaches infinity. The series does not fit standard geometric or alternating series patterns, so the ratio test is applied. Simplifying the expression reveals that the series converges for -5 < x < 5, with x = -5 included at the boundary, while x = 5 results in divergence. The video concludes with a clear interval of convergence for the series.
Takeaways
- 🔍 The goal of the video is to determine the interval of convergence for the given infinite series.
- 📊 The series doesn't fit neatly into geometric or alternating series categories, prompting the use of the ratio test.
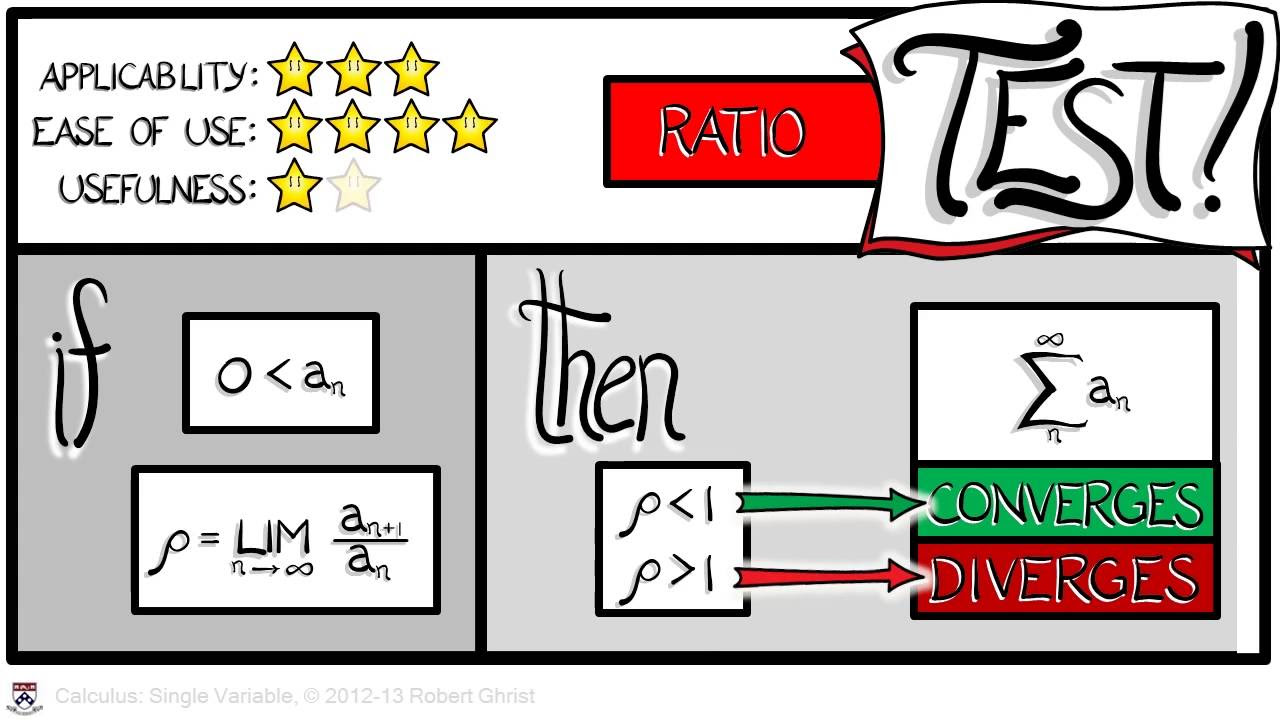
- ➗ The ratio test involves evaluating the limit as n approaches infinity of the absolute value of the (n+1)th term divided by the nth term.
- 📉 If the result of the ratio test is less than 1, the series converges; if it's greater than 1, the series diverges; if it's equal to 1, the test is inconclusive.
- 🔢 Simplifying the limit expression yields the absolute value of (x/5).
- 📏 The series converges when the absolute value of (x/5) is less than 1, implying -5 < x < 5.
- 🤔 When the absolute value of (x/5) equals 1, the test is inconclusive, requiring further examination of x = 5 and x = -5.
- 📉 For x = 5, the series becomes a harmonic series, which diverges.
- 🔄 For x = -5, the series becomes an alternating harmonic series, which converges by the alternating series test.
- ✅ The final interval of convergence is -5 <= x < 5, including x = -5 due to convergence.
Q & A
What is the main goal of the video?
-The main goal of the video is to determine the interval of convergence for an infinite series.
Why is the ratio test chosen to analyze the series?
-The ratio test is chosen because it is a general method that can be applied when the series does not fit cleanly into geometric or alternating series.
What does the ratio test involve?
-The ratio test involves taking the limit as n approaches infinity of the absolute value of the (n+1)th term divided by the nth term. If this limit is less than one, the series converges; if greater than one, it diverges; and if equal to one, the test is inconclusive.
How is the limit of the ratio test expression simplified?
-The limit expression is simplified by canceling out common terms and dividing both numerator and denominator by n, resulting in the absolute value of x over 5.
What is the condition for convergence derived from the ratio test?
-The series converges when the absolute value of x over 5 is less than one, which simplifies to the interval -5 < x < 5.
What needs to be considered beyond the ratio test for the interval of convergence?
-We need to consider the boundary points where the ratio test is inconclusive, i.e., when the absolute value of x over 5 equals one, meaning x equals 5 or -5.
What happens when x equals 5?
-When x equals 5, the series becomes the harmonic series, which is known to diverge.
What happens when x equals -5?
-When x equals -5, the series becomes an alternating harmonic series, which converges.
What is the final interval of convergence for the series?
-The final interval of convergence for the series is [-5, 5), meaning the series converges for all x in this range including -5 but excluding 5.
How can the alternating harmonic series be tested for convergence?
-The alternating harmonic series can be tested for convergence using the alternating series test, which confirms convergence if the terms are monotonically decreasing and their limit approaches zero.
Outlines
📚 Applying the Ratio Test to Determine Convergence
The instructor introduces the concept of determining the interval of convergence for an infinite series that does not fit into standard forms like geometric or alternating series. The focus is on using the ratio test, which involves calculating the limit of the absolute value of the (n+1)th term over the nth term as n approaches infinity. The goal is to find the range of x values for which the series converges. The process involves simplifying the ratio to a form that can be evaluated at infinity, which in this case results in x/5. The instructor emphasizes the need to consider when this value is less than one (indicating convergence), greater than one (indicating divergence), or equal to one (inconclusive and requiring further analysis).
🔍 Testing Boundary Points and Concluding the Interval of Convergence
This paragraph delves into the inconclusive cases identified by the ratio test, specifically when x equals ±5. The instructor tests these boundary points by substituting them into the series and analyzing the resulting series. For x=5, the series simplifies to a harmonic series, which is known to diverge. For x=-5, the series becomes an alternating harmonic series, which is shown to converge using the alternating series test. The instructor concludes that the interval of convergence for the series includes values of x greater than or equal to -5 and less than 5, thus establishing the final interval of convergence as (-5, 5).
Mindmap
Keywords
💡Infinite Series
💡Convergence
💡Ratio Test
💡Limit
💡Absolute Value
💡Geometric Series
💡Alternating Series
💡Harmonic Series
💡p-Series
💡Alternating Series Test
💡Interval of Convergence
Highlights
The goal is to determine the interval of convergence for an infinite series.
The series does not fit neatly into a geometric or alternating series, suggesting the ratio test should be used.
The ratio test involves taking the limit of the absolute value of the (n+1)th term divided by the nth term as n approaches infinity.
If the limit is less than one, the series converges; if greater than one, it diverges; if equal to one, the result is inconclusive.
The limit simplifies to x/5 by dividing numerator and denominator by n and recognizing 5/n approaches zero.
The series converges when the absolute value of x/5 is less than one, leading to the inequality -5 < x < 5.
The inconclusive cases occur when x/5 equals one or negative one, which translates to x = 5 or x = -5.
Testing x = 5 shows the series diverges, as it becomes a harmonic series which is known to diverge.
For x = -5, the series becomes an alternating harmonic series, which is shown to converge.
The interval of convergence is therefore -5 ≤ x < 5, including the boundary at x = -5 but not x = 5.
The ratio test provides a general method for determining convergence without fitting into specific series types.
The simplification process involves dividing by the highest power of n present in both the numerator and denominator.
The limit's behavior as n approaches infinity is crucial for applying the ratio test effectively.
The ratio test's outcome can be used to establish the boundaries of the interval of convergence.
Inconclusive cases from the ratio test require further analysis using other convergence tests.
The p-series divergence test confirms the divergence of the series when x = 5.
The alternating series test confirms the convergence of the series when x = -5.
The final interval of convergence is established by including the boundary points where the series behavior changes.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: