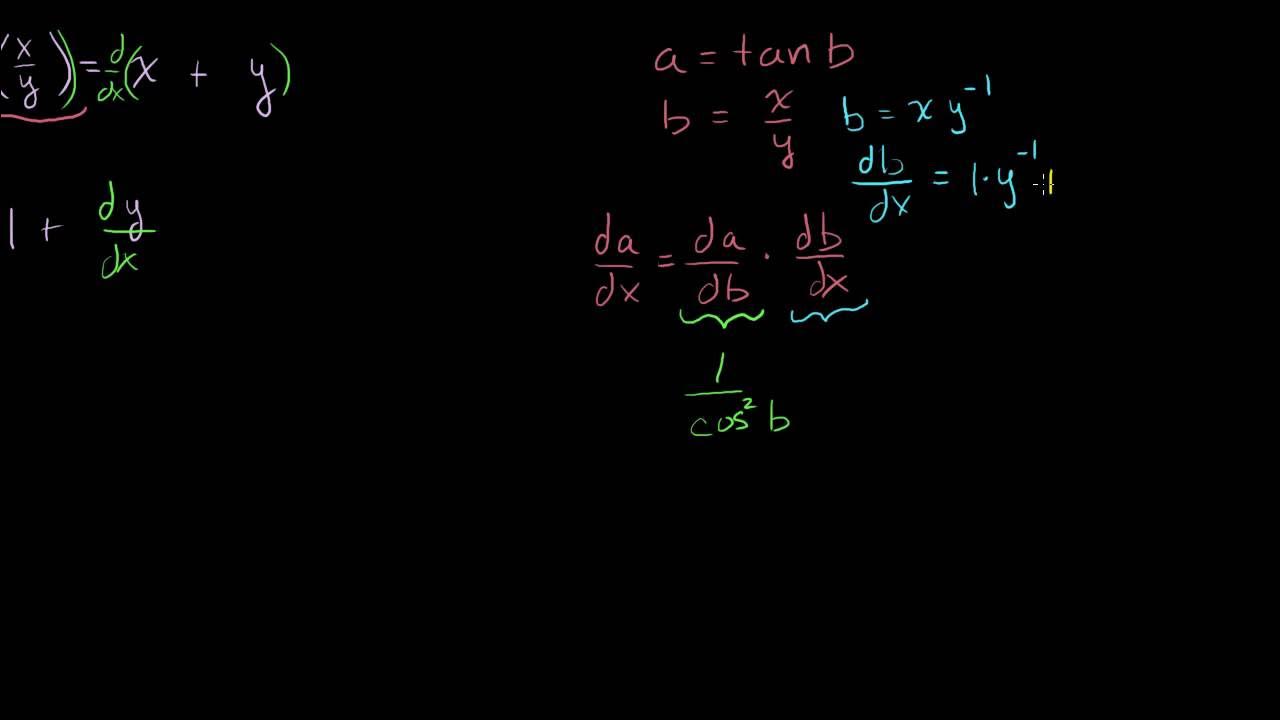Why do you divide by dx/dt when determining the concavity of a parametric curve?

RH Mathematics
12 Feb 202205:12
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter addresses a common question about the second derivative of y with respect to x, particularly in the context of parametric curves and concavity. The focus is on the step of dividing by dx/dt, which often confuses students. The explanation delves into the quotient rule and chain rule, illustrating why dividing by the rate of change of x with respect to t (dx/dt) is necessary. The presenter simplifies the complex process, clarifying the mathematical intuition behind the step and providing a clearer understanding of the concept.

Takeaways
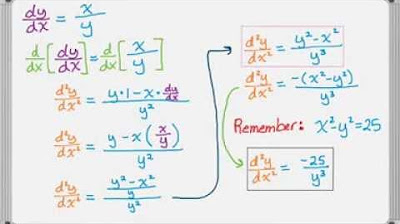
  • 📚 The video discusses the formula for the second derivative of y with respect to x, which is used to determine the concavity of a parametric curve.
  • 🤔 The script addresses a common question about why the derivative involves dividing by \( \frac{dx}{dt} \).
  • 📉 The formula for the second derivative involves taking the derivative of \( \frac{dy}{dx} \) with respect to t, and then dividing by \( \frac{dx}{dt} \).
  • 🔄 The process involves using the quotient rule and understanding the derivative of \( \frac{dy}{dt} \) over \( \frac{dx}{dt} \) with respect to x.
  • 🔍 The video script delves into the implicit derivative situation where both the numerator and denominator are functions of t.
  • 📐 The quotient rule is applied, factoring out \( \frac{dt}{dx} \) and considering the reciprocal relationship between \( \frac{dt}{dx} \) and \( \frac{dx}{dt} \).
  • 🧩 The script breaks down the complex process into understandable parts, highlighting the role of each component in the formula.
  • 🔑 The key takeaway is that dividing by \( \frac{dx}{dt} \) is necessary due to the application of the quotient rule and chain rule in the derivative process.
  • 📝 The video aims to provide a clearer, more rigorous explanation for the mathematical process behind the second derivative in parametric form.
  • 💡 The script suggests an intuitive understanding of the rates of change and their reciprocal relationship in the context of parametric derivatives.
  • 👨‍🏫 The video is a response to a question that arose in the classroom, aiming to clarify a concept that wasn't fully explained in advanced calculus courses.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is explaining why, in the context of finding the second derivative of y with respect to x in a parametric curve, one divides by dx/dt.

  • What is the formula for the second derivative of y with respect to x in a parametric curve?

    -The formula involves taking the derivative of dy/dx with respect to t. This is done by using the quotient rule on the expression dy/dx = y'(t)/x'(t).

  • Why is the quotient rule used in this context?

    -The quotient rule is used because dy/dx in a parametric context is a ratio of two functions of t (y'(t) and x'(t)), and taking the derivative of this ratio requires the application of the quotient rule.

  • What is the significance of dx/dt in the formula?

    -dx/dt is significant because it represents the rate of change of x with respect to t. It is used in the denominator of the formula, indicating its role in adjusting the rate of change of y with respect to t.

  • Why is dx/dt in the denominator of the formula?

    -dx/dt is in the denominator because it is part of the quotient rule application. It adjusts the derivative of dy/dx with respect to t, ensuring the correct rate of change is calculated.

  • What is the role of the derivative of t with respect to x in the formula?

    -The derivative of t with respect to x is used in the numerator of the formula. It represents the rate of change of t as x changes, which is crucial in the context of the parametric curve.

  • How does the video script address the question of dividing by dx/dt?

    -The script explains that dividing by dx/dt is necessary due to the application of the quotient rule and the chain rule, both of which are involved in finding the derivative of dy/dx with respect to t.

  • What is the relationship between the rate of change of t with respect to x and the rate of change of x with respect to t?

    -The rate of change of t with respect to x is the reciprocal of the rate of change of x with respect to t. This relationship is used to simplify the formula by flipping the ratio.

  • Why is the script's explanation considered more rigorous than simply multiplying ds and ts?

    -The script's explanation is more rigorous because it delves into the mathematical principles behind the quotient rule and the chain rule, rather than just manipulating symbols, which can be less clear and potentially misleading.

  • What is the conclusion of the video regarding the division by dx/dt?

    -The conclusion is that dividing by dx/dt is a necessary step in the process of finding the second derivative of y with respect to x in a parametric curve, as it correctly accounts for the rates of change involved.

Outlines
00:00
📚 Understanding the Second Derivative of y with Respect to x

This paragraph delves into the mathematical concept of the second derivative of y with respect to x, which is essential for analyzing the concavity of parametric curves. The speaker addresses a common question regarding the division by dx/dt in the formula. The explanation involves revisiting the derivative of dy/dx with respect to t and using the quotient rule to derive the second derivative. The process includes factoring out dt/dx and recognizing the reciprocal relationship between the rate of change of t with respect to x and x with respect to t. The final step involves applying the quotient rule and chain rule to arrive at the second derivative, which is then divided by dx/dt, providing a clear rationale for this step in the calculation.

05:01
🔍 Addressing a Lingering Question on Parametric Derivatives

The second paragraph wraps up the video by summarizing the main focus, which is to answer a lingering question that has arisen in the classroom regarding the division by dx/dt in the calculation of the second derivative of y with respect to x in a parametric context. The speaker emphasizes the importance of understanding the mathematical principles behind this division and provides a brief overview of the process discussed in the video, which includes the application of the quotient rule and the chain rule to derive the second derivative.

Mindmap
Keywords
💡Second derivative
The second derivative of a function is the derivative of the derivative. It measures the rate of change of the rate of change. In the context of the video, the second derivative of y with respect to x is used to determine the concavity of a parametric curve. The script mentions finding this derivative by taking the derivative of \( \frac{dy}{dx} \) with respect to t, which is crucial for understanding how the curve bends.
💡Parametric curve
A parametric curve is a curve defined by a set of parametric equations. These equations describe how the coordinates of points on the curve change as a parameter (often time) varies. The video discusses determining the concavity of such curves, which is essential for understanding the curve's shape and behavior.
💡Concavity
Concavity refers to the curvature of a function or curve. A curve is concave up if it bends upwards and concave down if it bends downwards. The video script discusses using the second derivative to determine the concavity of a parametric curve, which helps in understanding the curve's shape and inflection points.
💡Quotient rule
The quotient rule is a fundamental theorem in calculus that describes how to differentiate a quotient of two functions. In the video, the quotient rule is used to find the derivative of \( \frac{dy}{dx} \) with respect to t, which involves differentiating the numerator and denominator separately and combining them in a specific way.
💡Derivative
A derivative in calculus is a measure of how a function changes as its input changes. The video script discusses taking the derivative of \( \frac{dy}{dx} \) with respect to t, which is a key step in finding the second derivative of y with respect to x.
💡Rate of change
The rate of change is a measure of how one quantity changes relative to another. In the video, the rate of change of y with respect to t is divided by the rate of change of x with respect to t, which is a crucial step in finding the derivative of \( \frac{dy}{dx} \).
💡Reciprocal
The reciprocal of a number is 1 divided by that number. The video script mentions that the rate of change of t with respect to x is the reciprocal of the rate of change of x with respect to t, which is a key insight in simplifying the derivative expression.
💡Chain rule
The chain rule is a fundamental theorem in calculus that allows you to differentiate a composite function. Although not explicitly mentioned in the script, the process of differentiating \( \frac{dy}{dx} \) with respect to t involves a chain of dependencies, similar to the chain rule.
💡Differentiation
Differentiation is the process of finding the derivative of a function. The video script discusses the process of differentiating \( \frac{dy}{dx} \) with respect to t, which is a complex process involving the quotient rule and understanding how variables change with respect to each other.
💡Differentials
Differentials, such as \( dx \) and \( dt \), represent infinitesimally small changes in variables. The script discusses how these differentials are manipulated in the process of finding the second derivative, particularly in the context of dividing by \( \frac{dx}{dt} \).
💡Implicit derivative
An implicit derivative is a derivative where the function is not explicitly solved for y. The video script discusses taking the derivative of \( \frac{dy}{dx} \) with respect to x in a parametric context, which is an example of an implicit derivative situation.
Highlights

Exploring the formula for the second derivative of y with respect to x, crucial for determining concavity of a parametric curve.

Addressing the common question of why the derivative involves dividing by dx/dt.

Clarifying the formula involves taking the derivative of dy/dx with respect to t.

Discussing the rate of change of y with respect to t divided by the rate of change of x with respect to t.

Using the quotient rule in the process of finding the second derivative.

Highlighting the need for rigorous proof beyond multiplying and canceling d's, t's, and variables.

The challenge of finding a direct explanation for dividing by dx/dt in existing resources.

The importance of understanding the quotient rule in the context of implicit derivatives.

Differentiating with respect to x while accounting for t's own derivative with respect to x.

Introducing the concept of the rate of change of t with respect to x being reciprocal to the rate of change of x with respect to t.

Applying the quotient rule formula in the context of parametric differentiation.

Factoring out dt/dx to simplify the expression for the second derivative.

The intuition behind the relationship between derivatives and reciprocal rates of change.

Finalizing the explanation by connecting the quotient rule and chain rule.

Concluding the video with a resolution to the lingering question of dividing by dx/dt.

Transcripts

Browse More Related Video

Second derivatives (implicit equations): find expression | AP Calculus AB | Khan Academy

2011 Calculus BC free response #1 (b & c) | AP Calculus BC | Khan Academy

AP Calculus BC Lesson 9.2

Second Derivative of Implicit Function

Trig Implicit Differentiation Example

Multivariable chain rule

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Second DerivativeParametric CurvesConcavity AnalysisCalculus ConceptsDerivative FormulaQuotient RuleChain RuleMath EducationConcept ClarificationTeaching AidEducational Video