Absolute Extrema
TLDRThis educational video explores the concept of absolute extrema in calculus, explaining how to find the maximum and minimum values of a continuous function on a closed interval. The instructor illustrates the process with diagrams and a step-by-step method, including identifying critical points, evaluating the function at endpoints and critical points, and selecting the extreme values. Special scenarios with zero or one interior critical point are also discussed, along with real-world applications like particle motion, to deepen understanding of the topic.
Takeaways
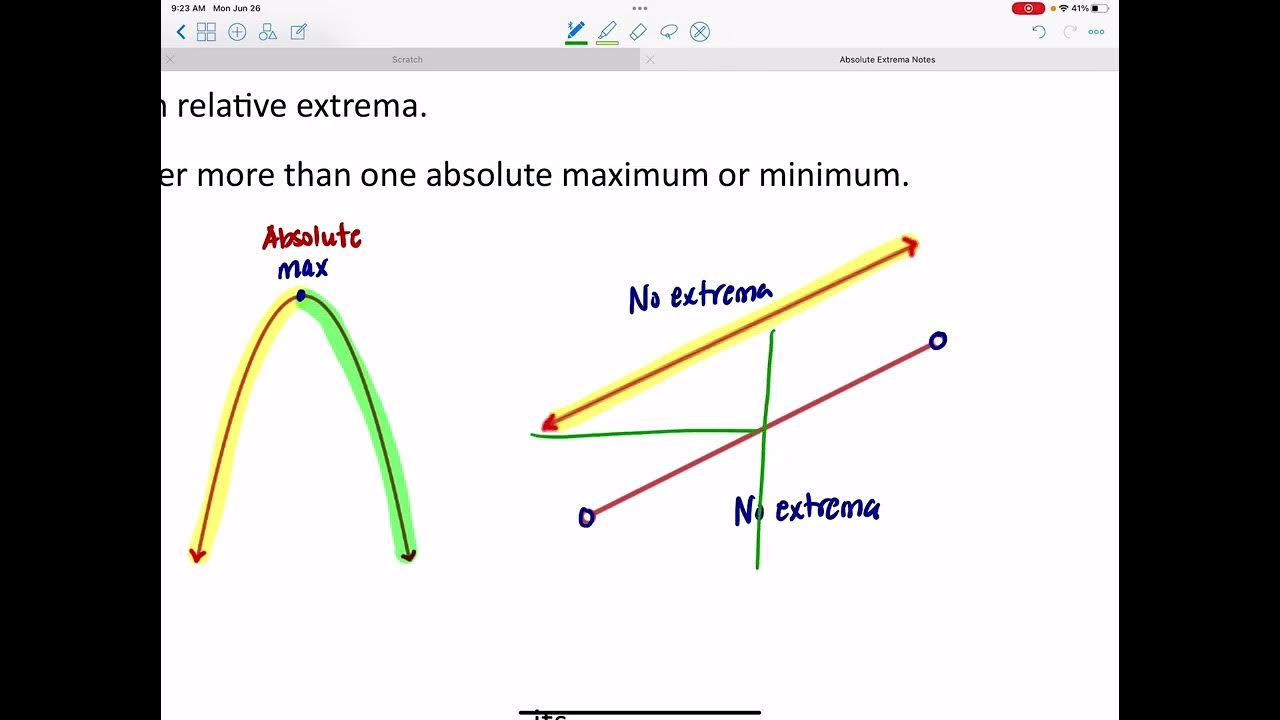
- 📚 A function that is continuous on a closed interval must have both a maximum and a minimum value on that interval.
- 🔍 The closed interval includes its endpoints, which is crucial for finding absolute extrema.
- 📈 The presence of a maximum or minimum is dependent on the function's continuity and the interval being closed; a lack of continuity or an open interval can prevent these from existing.
- 🔑 To find absolute extrema, one must look at endpoints and critical points, which are where the derivative is zero or does not exist.
- 📝 The process for finding absolute maxima and minima involves identifying critical points, evaluating the function at these points and the endpoints, and then selecting the maximum or minimum value from the evaluated list.
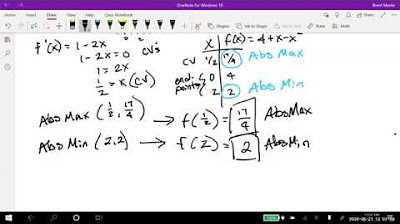
- 📉 In the given example, the minimum value of the function f(x) = x^3 - 12x + 25 on the interval [-5, 3] is found by evaluating the function at critical points and endpoints, then selecting the smallest value.
- 🤔 The 'candidate's test' or 'closed interval test' is a method to determine absolute extrema by evaluating the function at potential candidate points and selecting the extremum.
- 🏁 Special cases with zero or one interior critical point may not require the full candidate's test, as the extremum may be at an endpoint or easily identifiable from the derivative's behavior.
- 🔄 Understanding the behavior of the derivative (e.g., always positive or negative) can quickly indicate where the function has its absolute minimum or maximum without extensive calculations.
- 🚀 The script provides practical examples, including a particle motion scenario, to illustrate the application of finding absolute extrema in real-world contexts.
- 📚 The importance of distinguishing between local extrema and absolute extrema is highlighted, with the latter being the focus of the script.
Q & A
What are absolute extrema in the context of a function?
-Absolute extrema refer to the maximum and minimum values that a continuous function can take on a closed interval. This means that if a function is continuous on a closed interval, it must achieve both a maximum and a minimum value within that interval.
What is a closed interval and why is it important for finding absolute extrema?
-A closed interval is an interval that includes its endpoints, denoted as [a, b]. It is important because for a function to have absolute extrema, it must be continuous on this closed interval, ensuring that it achieves both a maximum and a minimum value.
What are the conditions under which a function does not necessarily have a maximum or minimum value?
-A function does not necessarily have a maximum or minimum value if it is not continuous on the interval or if the interval is not closed. Discontinuities or open intervals can prevent a function from achieving an absolute extremum.
How can you identify the locations of absolute extrema for a function?
-Absolute extrema occur at endpoints or critical points of the function. Critical points are where the derivative of the function is zero or does not exist.
What is the first step in finding absolute extrema of a function on a closed interval?
-The first step is to identify the critical points of the function. This involves finding where the derivative of the function is equal to zero or where the derivative is undefined.
What is the second step in the process of finding absolute extrema?
-The second step is to evaluate the function at each critical point and at the endpoints of the closed interval.
How do you determine the absolute extrema from the evaluated function values?
-After evaluating the function at critical points and endpoints, you compare these values to determine the maximum or minimum value, depending on what you are looking for.
What is the 'candidates test' or 'closed interval test' in the context of finding absolute extrema?
-The 'candidates test' or 'closed interval test' is the process of checking the function values at endpoints and critical points to find the absolute extrema. It is based on the principle that absolute extrema can only occur at these points.
Can a function have an absolute minimum value without having an absolute maximum value on a closed interval?
-No, if a function is continuous on a closed interval, it must have both an absolute minimum and an absolute maximum value on that interval.
What is a special situation where the 'candidates test' might not be necessary?
-A special situation where the 'candidates test' might not be necessary is when there is only one interior critical point or no interior critical points at all. In such cases, the function's behavior can be more easily determined without evaluating all endpoints and critical points.
Outlines
📚 Introduction to Absolute Extrema
The video begins with an introduction to the concept of absolute extrema, explaining that a continuous function on a closed interval must have both a maximum and a minimum value. The presenter uses visual illustrations to demonstrate how these extrema can occur at critical points or at the endpoints of the interval. The importance of continuity and the closed nature of the interval is emphasized, as these conditions are necessary for the existence of absolute extrema. The video also touches on the absence of extrema in cases where the function is not continuous or the interval is not closed.
🔍 Steps to Find Absolute Extrema
The presenter outlines a step-by-step process for finding absolute extrema. The first step is to identify critical points, which are locations where the derivative of the function is zero or undefined. The second step involves evaluating the function at these critical points and at the endpoints of the interval. The final step is to determine the maximum or minimum value from the evaluated function values. This method, often referred to as the 'candidate's test' or 'closed interval test', ensures that all potential extrema are considered.
📉 Example: Minimum Value of a Function
The video provides a practical example of finding the minimum value of the function f(x) = x^3 - 12x + 25 on the closed interval [-5, 3]. The presenter calculates the derivative, identifies critical points, and evaluates the function at these points and at the interval endpoints. A table is used to organize the values, and the minimum value is determined by comparing them. The conclusion is that the minimum value of the function on the given interval is -80, which occurs at x = 2.
🏁 Special Cases with Few Critical Points
The presenter discusses special cases where the function has zero or one interior critical point. In such cases, the absolute extrema can be determined without running the full candidate's test. Examples include a function where the derivative is always positive, indicating that the function only increases and thus has its minimum at x = 0, and a particle motion scenario where the velocity function is only negative before a certain time and only positive after, indicating the farthest left position at that time. The video concludes with a reminder to consider these special cases when solving problems involving absolute extrema.
Mindmap
Keywords
💡Absolute Extrema
💡Closed Interval
💡Critical Points
💡Derivative
💡Continuous Function
💡Endpoint
💡Candidate's Test
💡Particle Motion
💡Velocity
💡Position Function
Highlights
Introduction to absolute extrema and the conditions for their existence on a closed interval.
Explanation of a closed interval including its endpoints for a function to have a maximum and minimum.
Visual representation of continuous functions on closed intervals with examples of maximum and minimum values.
The necessity of continuity for a function to have absolute extrema on a closed interval.
Illustration of how a lack of continuity can affect the existence of maximum and minimum values.
The concept of critical points in determining absolute extrema and their definition.
Steps for finding absolute maximum and minimum values, starting with identifying critical points.
Evaluation of the function at critical points and endpoints to determine extrema.
The 'candidates test' or 'closed interval test' as a method for finding absolute extrema.
Example problem: Finding the minimum value of a cubic function on a specified closed interval.
Demonstration of the process to find the minimum value through calculation and comparison.
Special cases where the candidates test may not be necessary due to the number of interior critical points.
Understanding the behavior of a function's derivative to infer the location of absolute extrema without the test.
Application of the concepts to a particle motion scenario to find the farthest left position.
Another particle motion example using an algebraic function to determine when the object is farthest to the right.
The importance of identifying the correct t-value for the farthest position in motion problems.
Declining to solve problems that are not typical for AP Calculus, focusing on the candidates test.
Conclusion emphasizing the ability to perform the candidates test and understand special cases of critical points.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: