Exponential decay formula proof (can skip, involves calculus) | Chemistry | Khan Academy
TLDRThis video script delves into the concept of half-life and its application in radioactive decay, particularly using carbon-14 as an example. It explains how the amount of a decaying substance can be determined over time, introducing a general function that relates the quantity of the substance to time. The script guides viewers through the mathematical derivation, using calculus to solve a differential equation and establish a formula that can predict the remaining amount of a substance at any given time. The process includes determining the decay constant, lambda, from the half-life, and applying it to calculate the substance's quantity at various time intervals.
Takeaways
- 🕒 The concept of half-life is useful for understanding decay over multiples of a half-life.
- 🧮 At time zero, we have 100% of the substance. After one half-life, 50% remains; after two half-lives, 25% remains.
- 🧪 Knowing the half-life, we can predict the amount of substance remaining after a specific time, such as 1/2 a year or 10 minutes.
- 📉 The rate of decay is proportional to the amount of the substance present.
- ✏️ The rate of change can be expressed as a differential equation: dN/dt = -λN, where λ is the decay constant.
- 📐 Solving the differential equation involves separation of variables and integration.
- 📈 The general solution to the differential equation is N(t) = N₀ * e^(-λt), where N₀ is the initial amount of substance.
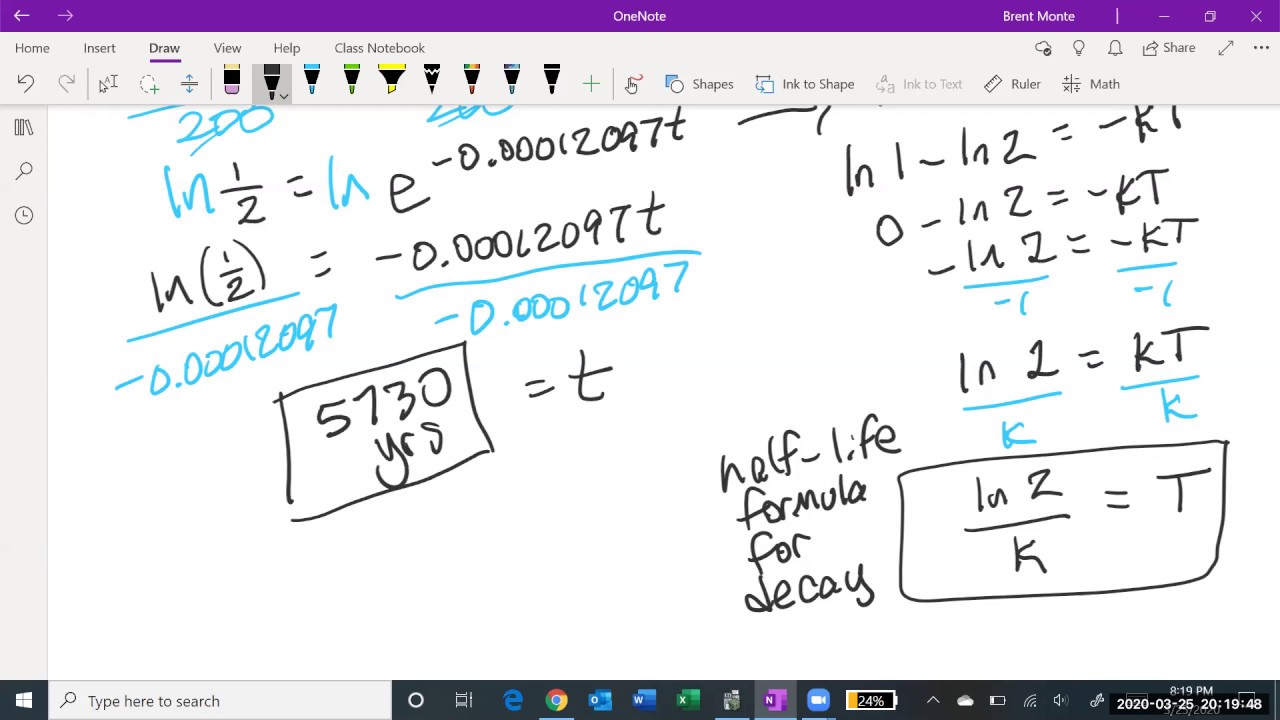
- 🧬 For carbon-14, which has a half-life of 5,700 years, the decay constant λ can be calculated as λ = ln(1/2) / -5700.
- 🔢 The specific decay constant for carbon-14 is approximately 1.21 * 10^-4 per year.
- 📊 Using the decay constant, we can determine the amount of carbon-14 remaining at any time t by plugging into the formula N(t) = N₀ * e^(-1.21 * 10^-4 * t).
Q & A
What is the concept of half-life and how is it used in decay processes?
-The half-life of a substance is the time it takes for half of the substance to decay. It's used to predict the amount of a substance remaining after a given period, particularly useful when the time increments are multiples of the half-life.
Why is it necessary to have a general function to describe substance decay over time?
-A general function is needed to describe the decay of a substance over any given time, not just multiples of the half-life. This allows for precise calculations of the remaining substance at any time, whether it's a fraction of a half-life or many half-lives.
What is the relationship between the rate of decay and the amount of substance present?
-The rate of decay is directly proportional to the amount of substance present. As the substance decreases, the rate of decay also decreases because there is less substance available to decay.
How does the script use calculus to model the decay of a substance?
-The script applies calculus, specifically differential equations and separation of variables, to model the decay process. By setting up an equation where the rate of change of the substance is proportional to the current amount, the script derives a general function to describe decay over time.
What is the differential equation derived from the decay process and how is it solved?
-The differential equation derived is \( \frac{1}{N} \frac{dN}{dt} = -\lambda \). It is solved by separating variables and integrating both sides, leading to the equation \( \ln(N) = -\lambda t + C \), which is then exponentiated to solve for \( N \) as a function of \( t \).
How is the constant lambda related to the half-life of a substance?
-The constant lambda is the decay constant and is related to the half-life (T) by the equation \( \lambda = \frac{\ln(2)}{T} \), where \( T \) is the half-life of the substance.
What is the general formula for the amount of a decaying substance as a function of time?
-The general formula is \( N(t) = N_0 e^{-\lambda t} \), where \( N_0 \) is the initial amount of the substance, \( \lambda \) is the decay constant, and \( t \) is the time.
How can the script's explanation of decay help in understanding the concept of carbon-14 dating?
-The script's explanation provides a mathematical model for decay, which is fundamental to carbon-14 dating. By knowing the half-life of carbon-14 and the decay constant, scientists can calculate the remaining amount of carbon-14 in a sample and estimate its age.
What is the significance of the natural logarithm in solving the decay differential equation?
-The natural logarithm is used to isolate the variable \( N \) and integrate the differential equation. It simplifies the equation to a form that can be exponentiated to solve for \( N \) as a function of time.
How does the script illustrate the concept of decay with an example of carbon atoms?
-The script uses an example of two samples with different amounts of carbon atoms to illustrate how the rate of decay is proportional to the number of atoms present. A larger sample will have a higher rate of decay events over a given time period compared to a smaller sample.
What is the role of the constant c4 in the final equation for decay?
-The constant c4 is an arbitrary constant that results from the integration process. It is later identified as \( N_0 \), the initial amount of the substance, when the equation is solved for a specific initial condition.
Outlines
🕰 Understanding Half-Life and Decay Rates
This paragraph introduces the concept of half-life and its utility in understanding radioactive decay. It explains how the amount of a substance decays over time, halving with each half-life period. The speaker proposes a general function to determine the amount of a decaying substance at any given time, which will be explored further in the video. The paragraph also touches on the rate of change and the proportional relationship between the decay and the amount of substance present, setting the stage for a mathematical exploration.
📚 Deriving the Decay Equation
The speaker dives into the mathematical derivation of the decay equation. They start by discussing the rate of change and how it is proportional to the amount of substance present. Using a differential equation, they show that the rate of decay is a negative exponential function of time. The solution involves integrating both sides of the equation, leading to a natural logarithm relationship. The final form of the equation is derived, showing that the amount of substance at any time t is equal to the initial amount multiplied by a decay factor, which is an exponential function of time.
🔍 Applying the Decay Equation to Carbon-14
In this paragraph, the speaker applies the derived decay equation to the specific case of carbon-14, which has a known half-life of 5,700 years. They use the half-life to determine the decay constant lambda, which is crucial for the equation. By setting the time to 5,700 years and the remaining amount to half of the initial, they solve for lambda and find its value. The paragraph concludes with the general equation for the amount of carbon-14 at any time t, demonstrating how the initial amount decays over time.
Mindmap
Keywords
💡Half-life
💡Radioactive decay
💡Exponential decay
💡Differential equation
💡Separation of variables
💡Integral
💡Antiderivative
💡Natural logarithm
💡Lambda (λ)
💡Carbon-14
💡Exponential function
Highlights
The concept of half-life is crucial for understanding the decay of substances over time.
At time equals zero, 100% of the substance is present, and it decays to 50% after one half-life.
The decay process can be generalized to any time frame, not just multiples of a half-life.
The rate of decay is proportional to the amount of substance present, which is a key insight for modeling.
The decay process can be modeled using calculus, specifically through differential equations.
The rate of change in the number of particles decaying is dependent on the current number of particles.
The decay rate constant varies depending on the substance, affecting the rate of decay.
A differential equation can be set up to model the decay process, involving the separation of variables.
The solution to the differential equation involves the natural logarithm and an exponential function.
The general solution for the decay of a substance can be expressed as N(t) = N₀ * e^(-λt), where N₀ is the initial amount.
The decay constant λ can be determined from the half-life of the substance.
For carbon-14, the half-life is approximately 5,700 years, which can be used to calculate λ.
The equation N(t) = N₀ * e^(-λt) allows for the calculation of the remaining substance at any given time t.
The relationship between the decay constant λ and the half-life is fundamental in nuclear physics.
The method presented can be applied to any radioactive decay process, not just carbon-14.
The mathematical model provides a precise way to predict the decay of radioactive substances over time.
The practical applications of this model include dating ancient artifacts and understanding geological processes.
Transcripts
Browse More Related Video

Introduction to exponential decay | Nuclear chemistry | Chemistry | Khan Academy

Half-life and carbon dating | Nuclear chemistry | Chemistry | Khan Academy
Math 11 - Section 2.5 (previously section 3.4)

Nuclear Half Life: Intro and Explanation

Half-Life and Radioactive Decay
Half Life Chemistry Problems - Nuclear Radioactive Decay Calculations Practice Examples
5.0 / 5 (0 votes)
Thanks for rating: