Half-Life and Radioactive Decay
TLDRIn this AP Physics essentials video, Mr. Andersen uses a dice-rolling simulation to illustrate the concept of half-life and radioactive decay. Starting with 32 dice, he demonstrates how the number of dice decreases by half each generation, analogous to the decay of radioactive nuclei. He explains that decay involves the emission of particles like alpha, beta, or gamma, leading to the formation of more stable nuclei while conserving mass and energy. The video covers the unpredictability of decay and uses the law of large numbers to calculate half-life, which is the time for half of the radioactive nuclei to decay. The script also discusses different types of decay, including alpha, beta, and gamma, providing examples like uranium-238 and carbon-14, and shows how half-life can be determined from a decay curve.
Takeaways
- 🎲 The script uses a dice-rolling simulation to illustrate the concept of radioactive decay and half-life.
- 🌟 The half-life is defined as the time it takes for half of a radioactive substance to decay.
- 📉 In the simulation, each generation represents a half-life period where a certain number of dice (representing radioactive nuclei) are removed.
- 🔢 The decay constant in the dice model is 1 in 6, which means there is a one-sixth chance that a dice (nucleus) will decay with each generation.
- ⚖️ The law of conservation of mass and energy is maintained during radioactive decay, with the mass and charge being conserved before and after the decay.
- 📈 The probability of decay is random and unpredictable for individual nuclei, but the law of large numbers allows for the calculation of half-life for a large number of nuclei.
- 📊 The formula ΔN = -λNt is used to calculate the change in the number of radioactive nuclei over time, where λ is the decay constant and t is time.
- 📚 The script explains how to use a spreadsheet to model the decay process and compare predicted decay to actual results in the simulation.
- 🕰 By changing the decay constant in the model, the rate of decay and thus the half-life can be altered, demonstrating how half-life is dependent on the decay constant.
- 📉 The script shows how to determine the half-life from a decay curve, by measuring the time it takes for the substance to decay to half of its original amount.
- 🌳 The principles of radioactive decay, including different types of decay (alpha, beta, gamma) and their respective half-lives, are used in practical applications such as dating organic materials and determining the age of the Earth.
Q & A
What is the concept of half-life in the context of radioactive decay?
-Half-life is the amount of time it takes for half of a radioactive substance to decay. It is a key concept in understanding how radioactive materials diminish over time.
How does the dice rolling simulation in the video relate to the concept of half-life?
-The dice rolling simulation is an analogy for radioactive decay. Each generation of dice represents a 'half-life' period where half of the remaining dice (representing radioactive atoms) are removed, mimicking the decay process.
What does it mean when it is said that radioactive nuclei decay by 'quick off' a particle?
-This phrase means that during decay, a radioactive nucleus will emit a particle, which could be an alpha, beta, or gamma particle. This emission leads to the formation of a new, usually more stable nucleus.
What principles are conserved during radioactive decay?
-Both mass and energy are conserved during radioactive decay. This means that the total amount of mass and energy before and after the decay process remains the same.
How can the law of large numbers be applied to calculate half-life?
-The law of large numbers allows for statistical averages to become more accurate as the sample size increases. In the context of half-life, it means that while we can't predict when a single nucleus will decay, we can predict the decay rate of a large number of nuclei over time.
What is the formula used to calculate the change in the number of radioactive nuclei?
-The formula used is ΔN = -λ * N * t, where ΔN is the change in the number of radioactive nuclei, λ is the decay constant, N is the number of radioactive nuclei, and t is time.
How does the decay constant relate to the probability of decay?
-The decay constant (λ) is a proportionality factor that relates to the probability of a nucleus decaying. It is used in the calculation of how many nuclei will decay over a given period of time.
What is the significance of the decay constant changing from one-sixth to one-half in the simulation?
-Changing the decay constant to one-half means that the rate of decay is doubled, so more dice (representing nuclei) will decay with each generation. This results in a shorter half-life, as it takes less time for all the dice to decay.
How can one determine the half-life from a decay curve?
-To determine the half-life from a decay curve, one should observe the time it takes for the quantity of the radioactive substance to reduce to half of its initial amount. This time interval represents the half-life of the substance.
What are the different types of particles that can be emitted during radioactive decay?
-During radioactive decay, three types of particles can be emitted: alpha particles (which consist of 2 protons and 2 neutrons), beta particles (which are electrons or positrons), and gamma rays (which are high-energy photons).
How is the half-life of a radioactive isotope used in dating materials?
-The half-life of a radioactive isotope, such as carbon-14, is used in dating materials by measuring the amount of the isotope remaining in a sample and comparing it to the original amount. This comparison allows scientists to estimate the age of the material.
What is the half-life of uranium-238 and how is it significant in determining the age of the Earth?
-The half-life of uranium-238 is approximately 4.47 billion years. This long half-life allows scientists to use uranium-238 to date extremely old rocks and, by extension, to estimate the age of the Earth.
Outlines
🎲 Understanding Radioactive Decay with Dice Simulation
In this segment, Mr. Andersen uses a dice rolling simulation to explain the concept of half-life and radioactive decay. The process involves starting with 32 dice and removing all dice that show a certain number (in this case, 1s), which represents one generation of decay. This is repeated over several generations until all dice have 'decayed'. The half-life is illustrated when half of the original dice (16 out of 32) are removed after four generations. The decay constant is introduced as the probability of decay per generation, which in this simulation is one-sixth, corresponding to the chance of rolling a 1. The video also discusses how mass and energy are conserved during decay and how the law of large numbers can be used to calculate half-life. The process is modeled using a spreadsheet, and the results are compared to the actual outcomes of the dice simulation, showing a close match.
📊 Calculating Half-Life and Types of Radioactive Decay
This paragraph delves into calculating the half-life of a radioactive isotope, using carbon-14 as an example. The half-life is determined by observing a decay curve and measuring the time it takes for half of the radioactive nuclei to decay. For carbon-14, the half-life is found to be approximately 6,000 years, which is consistent across multiple generations. The video then explores different types of radioactive decay: alpha decay, where an alpha particle (consisting of 2 protons and 2 neutrons) is emitted, beta decay, where a neutron is converted into a proton with the emission of an electron and an electron antineutrino, and gamma decay, which involves the emission of gamma rays. The half-lives of uranium-238 (4.47 billion years) and barium-137 (2.6 minutes) are also discussed, illustrating the wide range of half-life durations. The video concludes by emphasizing the importance of understanding how to interpret decay curves to determine half-life.
Mindmap
Keywords
💡Half-life
💡Radioactive decay
💡Decay constant
💡Alpha decay
💡Beta decay
💡Gamma decay
💡Conservation of mass
💡Conservation of charge
💡Law of large numbers
💡Radioactive dating
Highlights
Introduction to the concept of half-life and radioactive decay using a dice rolling simulation.
Explanation of the half-life as the time it takes for half of a radioactive substance to decay.
Demonstration of the dice simulation with the removal of dice representing decayed radioactive nuclei.
Observation that the half-life remains consistent throughout the decay process.
Description of radioactive decay involving the emission of alpha, beta, or gamma particles.
Conservation of mass and energy during radioactive decay.
Use of the law of large numbers to calculate half-life probabilities.
Introduction of the equation to calculate decay at each generation.
Explanation of the decay constant and its role in the decay process.
Application of the decay formula using a spreadsheet example.
Comparison of predicted decay with actual simulation results.
Impact of changing the decay constant on the rate of decay and half-life.
Calculation of half-life from a graph as demonstrated with carbon-14.
Different types of radioactive decay: alpha, beta, and gamma.
Conservation of mass and charge in alpha and beta decay examples.
Practical application of half-life in dating materials, such as carbon dating.
Explanation of how the half-life of uranium-238 is used to determine the age of the Earth.
Overview of the short half-life of gamma decay in barium-137.
Transcripts
Browse More Related Video

Nuclear Physics: Crash Course Physics #45
Radioactivity, Half-Life & Inverse Square Law - GCSE & A-level Physics (full version)

radioactivity explained
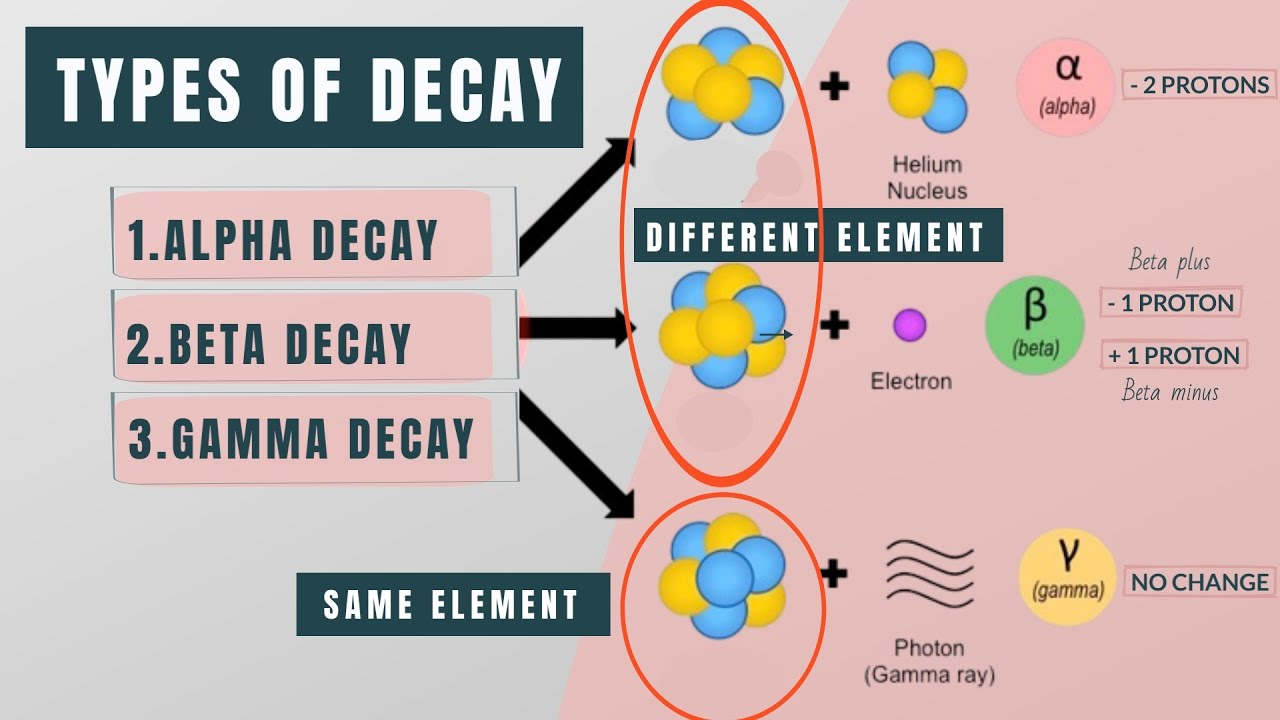
Different types of decay | Alpha vs. Beta vs. Gamma decay | Visual Explanation

Half-life and carbon dating | Nuclear chemistry | Chemistry | Khan Academy

Alpha Decay, Beta Decay, Gamma Decay - Electron Capture, Positron Production - Nuclear Chemistry
5.0 / 5 (0 votes)
Thanks for rating: