Introduction to exponential decay | Nuclear chemistry | Chemistry | Khan Academy

Khan Academy
11 Sept 200909:19
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores the concept of half-lives and how they relate to the decay of elements like carbon-14. It delves into the exponential decay formula, demonstrating how to calculate the remaining amount of a substance after a given time and how to determine the time needed for a substance to decay to a certain level. The script uses carbon-14 as an example, showing calculations for both scenarios.

Takeaways
  • 📚 The script discusses the concept of half-lives and how they are useful for determining the amount of a compound remaining after a certain number of half-lives.
  • 🔍 Half-life calculations are not as helpful for determining the amount of a compound after non-integer multiples of half-lives or arbitrary time periods.
  • 📉 The script introduces a formula to calculate the amount of a decaying element at any given time, involving the initial amount, the constant 'k', and time 't'.
  • 🧮 The formula is derived using calculus, and the script suggests that viewers unfamiliar with calculus can skip the derivation.
  • 🌐 The script provides a practical example using Carbon-14, which has a half-life of 5,730 years, to demonstrate how to apply the formula.
  • ⚗️ By using the half-life of Carbon-14, the script shows how to solve for the decay constant 'k', which is essential for the formula.
  • 🔑 The script emphasizes that the value of 'k' is specific to each element and its half-life, and once determined, it can be used in the formula for that element.
  • 🕰️ An example calculation is provided to find out how much Carbon-14 remains after 2000 years, using the derived formula and the decay constant.
  • 🔢 The script also demonstrates how to use the formula to calculate the time it takes for a certain amount of Carbon-14 to decay to a specific quantity.
  • 🛠️ The importance of understanding the exponential decay formula is highlighted, as it allows for the calculation of substance amounts after non-standard time periods.
  • 🔄 The script concludes by encouraging viewers to remember the formula and to apply it to various problems involving radioactive decay.
Q & A

  • What is the main topic discussed in the video script?

    -The main topic discussed in the video script is the concept of half-lives and the mathematical formula used to calculate the decay of radioactive elements, specifically focusing on Carbon-14.

  • Why are half-lives useful in understanding compound decay?

    -Half-lives are useful because they provide a straightforward way to estimate how much of a compound remains after a certain number of half-lives, making it easier to predict the decay process.

  • What is the limitation of using half-lives for calculating decay over non-integer multiples of half-lives?

    -The limitation is that half-lives are not as useful for calculating the decay over non-integer multiples of half-lives, such as after 1/2 of a half-life, one day, or 10 seconds, because they do not provide precise values for these specific time periods.

  • What mathematical formula is used to describe the decay of a radioactive element?

    -The formula used to describe the decay of a radioactive element is N(t) = N₀ * e^(-kt), where N(t) is the amount of the element at time t, N₀ is the initial amount, k is a decay constant, and e is the base of the natural logarithm.

  • How is the decay constant (k) related to the half-life of an element?

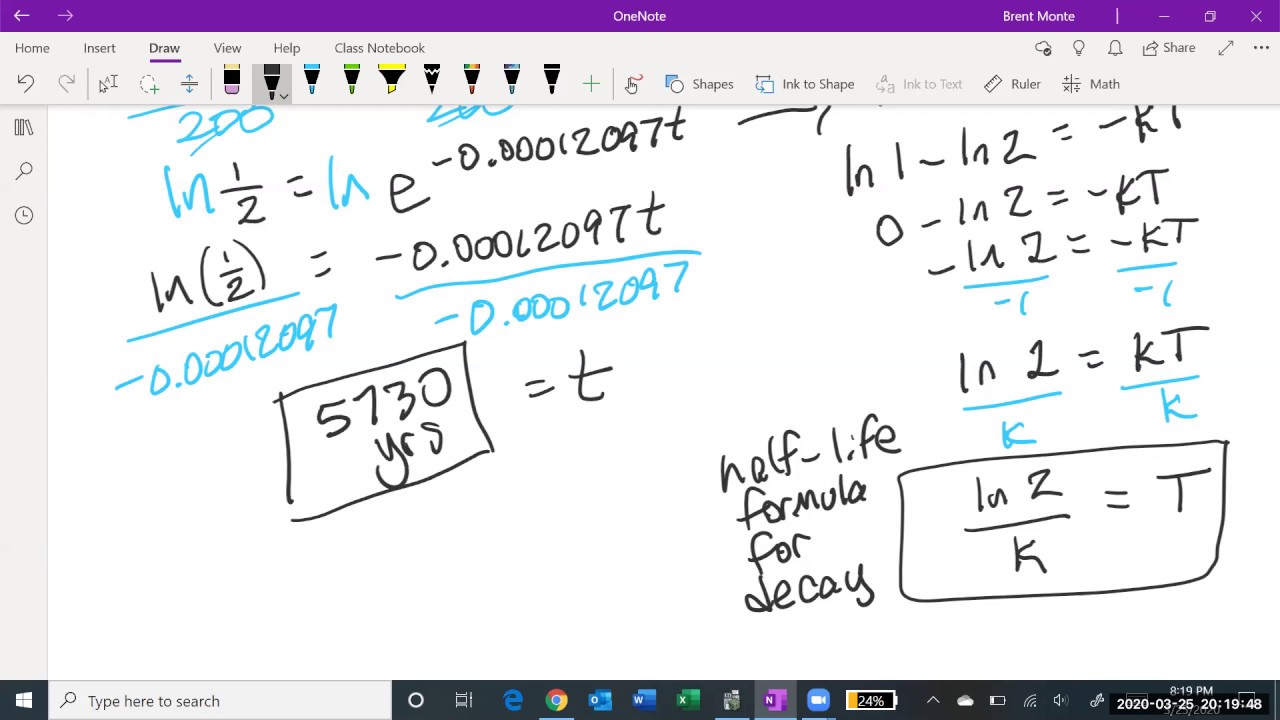
    -The decay constant (k) is related to the half-life (t) of an element by the formula k = ln(1/2) / t. This allows you to calculate the decay constant for any element given its half-life.

  • What is the half-life of Carbon-14?

    -The half-life of Carbon-14 is 5,730 years.

  • How can you calculate the decay constant (k) for Carbon-14 using its half-life?

    -You can calculate the decay constant (k) for Carbon-14 by taking the natural logarithm of 1/2 and dividing it by the half-life (5,730 years), resulting in k = ln(1/2) / 5,730 ≈ 1.2 * 10^-4 per year.

  • How much Carbon-14 would remain after 2000 years if you start with 300 grams?

    -Using the formula N(t) = N₀ * e^(-kt), you can calculate that after 2000 years, the amount of Carbon-14 remaining would be approximately 236 grams, starting from an initial 300 grams.

  • How long would it take for 400 grams of Carbon-14 to decay to 350 grams?

    -By rearranging the decay formula and solving for time, you can determine that it would take approximately 1,112 years for 400 grams of Carbon-14 to decay to 350 grams.

  • Why is it important to understand the exponential decay formula in the context of radioactive decay?

    -Understanding the exponential decay formula is important because it allows you to calculate the amount of a radioactive substance remaining at any given time, which is crucial in fields such as archaeology, geology, and nuclear physics.

Outlines
00:00
📚 Understanding Radioactive Decay with Half-Lives

This paragraph introduces the concept of half-lives in the context of radioactive decay. It explains that while half-lives are useful for determining the remaining amount of a compound after exact multiples of half-lives, they are less practical for other time intervals. The speaker references a previous video that proved a formula for radioactive decay, which involves calculus and may not be necessary for an introductory math class. The formula is presented as the amount of an element at any time being equal to the initial amount multiplied by \( e \) to the power of a constant minus the product of the constant and time. The paragraph then focuses on applying this formula to carbon-14, with a half-life of 5,730 years, to derive the decay constant 'k' and use it in the formula.

05:03
🔍 Applying the Radioactive Decay Formula to Carbon-14

In this paragraph, the speaker demonstrates how to apply the radioactive decay formula to carbon-14 to solve for the amount of the substance remaining after a given time and to calculate the time it takes for the substance to decay to a certain amount. The speaker uses the formula with the decay constant for carbon-14, which was derived from its half-life, to calculate the remaining amount of 300 grams of carbon-14 after 2000 years. The result is approximately 236 grams. Additionally, the speaker shows how to use the formula to find out how long it would take for 400 grams of carbon-14 to decay to 350 grams, which is calculated to be 1112 years. The paragraph emphasizes the importance of understanding and remembering the decay formula and its derivation for solving such problems.

Mindmap
Keywords
💡Half-life
Half-life refers to the time required for half of a given quantity of a radioactive substance to decay. In the context of the video, it is fundamental to understanding how much of a compound remains after a certain period. The script uses the half-life of Carbon-14, which is 5,730 years, to demonstrate the decay formula and its application.
💡Compound
A compound in this script refers to a substance, such as Carbon-14, that undergoes radioactive decay. The script explains how to calculate the remaining amount of a compound after a given time, emphasizing the importance of understanding compounds in the study of radioactive decay.
💡Exponential decay
Exponential decay is a mathematical process where a quantity decreases at a rate proportional to its current value, as seen in radioactive decay. The video script introduces a formula to calculate the decay of a substance over time, which is essential for understanding the concept of exponential decay.
💡Carbon-14
Carbon-14 is a radioactive isotope of carbon used for dating organic materials. The script specifically discusses Carbon-14 to illustrate the decay formula, using its known half-life to solve for the decay constant 'k' and apply it to various decay scenarios.
💡Decay constant (k)
The decay constant 'k' is a rate at which a radioactive substance decays. The script derives the value of 'k' for Carbon-14 by using its half-life, showing how 'k' is crucial for calculating the remaining substance after a given time.
💡Natural logarithm
The natural logarithm is a logarithm to the base 'e' and is used in the script to solve for the decay constant 'k'. It is an essential mathematical tool in the process of deriving the formula for radioactive decay.
💡e (Euler's number)
Euler's number 'e' is an important mathematical constant approximately equal to 2.71. In the script, 'e' is used as the base of the exponent in the decay formula, representing the natural growth or decay rate in exponential functions.
💡Radioactive dating
Radioactive dating is a technique used to determine the age of materials by measuring the decay of radioactive isotopes. The script uses the decay of Carbon-14 to demonstrate how to calculate the remaining amount of a substance, which is a fundamental concept in radioactive dating.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change. The script mentions calculus in the context of deriving the decay formula, indicating that while it is not necessary for an introductory math class, it is used to understand the underlying mathematics of radioactive decay.
💡Scientific calculator
A scientific calculator is a device used for performing complex mathematical calculations, including those involving exponential functions. The script refers to the need for a scientific calculator to compute the value of 'e' raised to a certain power, which is part of the decay formula calculation.
💡Time variable (t)
In the context of the script, the time variable 't' represents the elapsed time in years or other units since the start of the decay process. It is a key component of the decay formula, used to calculate the amount of substance remaining after a certain period.
Highlights

Introduction to half-life and its limitations in calculating compound amounts after non-integer half-life periods.

Explanation of a mathematical formula for calculating the decay of an element at any given time.

Use of the constant 'k' to represent the decay rate in the formula.

Demonstration of solving for 'k' using the half-life of Carbon-14.

Application of the formula to calculate the remaining amount of Carbon-14 after a specific time period.

Derivation of the general formula for Carbon-14 decay using its half-life.

Calculation of the remaining Carbon-14 after 2000 years from an initial 300 grams.

Use of a scientific calculator to determine the decay factor e^(-0.2419).

Result of the calculation showing 236 grams of Carbon-14 remaining after 2000 years.

Introduction of a problem-solving scenario to find the time needed for 400 grams of Carbon-14 to decay to 350 grams.

Process of solving for time using the decay formula and the given initial and final amounts.

Calculation of the time required for the decay from 400 to 350 grams of Carbon-14.

Explanation of the importance of remembering the decay formula for solving similar problems.

Emphasis on the practicality of the formula for any element by solving for its 'k' value.

Announcement of further problem-solving examples in the next video.

Transcripts

Browse More Related Video

Exponential decay formula proof (can skip, involves calculus) | Chemistry | Khan Academy

Math 11 - Section 2.5 (previously section 3.4)

Half-life and carbon dating | Nuclear chemistry | Chemistry | Khan Academy

Radioactivity, Half-Life & Inverse Square Law - GCSE & A-level Physics (full version)

15.4 Kinetics of Nuclear Decay | High School Chemistry

Nuclear Half Life: Intro and Explanation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Radioactive DecayHalf-LifeCarbon-14Exponential DecayMathematicsScience EducationCalculusElement DatingTime CalculationE-formula