Choosing Which Convergence Test to Apply to 8 Series
TLDRThis video script offers a comprehensive guide on identifying and applying the appropriate convergence tests to various mathematical series. The presenter introduces eight different series and matches them with suitable tests, such as the geometric series test, interval test, alternating series test, divergence test, comparison test, limit comparison test, root test, and ratio test. The script explains the rationale behind choosing each test and provides a quick method selection strategy. The video concludes with a full solution for each series, encouraging viewers to fast-forward for specific answers but focusing on the selection process rather than the solutions themselves.
Takeaways
- 📚 The video discusses 8 different series tests to determine their convergence or divergence.
- 🔍 The geometric series test is applied to series with a fixed ratio, and the script provides an example with a ratio of 2/5.
- 📉 The interval test and integral test are used for series that can be represented by a function, with an example of an improper integral of an exponential function.
- 🔄 The alternating series test is applicable to series with a decreasing, positive term that approaches zero, and only one of the two candidates meets the criteria.
- 🚫 The divergence test checks if the sequence does not converge to zero, indicating the series diverges, exemplified by a logarithmic sequence.
- ⚖️ The comparison test and limit comparison test are used for series that can be compared to a known convergent series, such as a p-series.
- 🔢 The root test is suitable for series with terms raised to the power of n, simplifying the limit calculation for convergence.
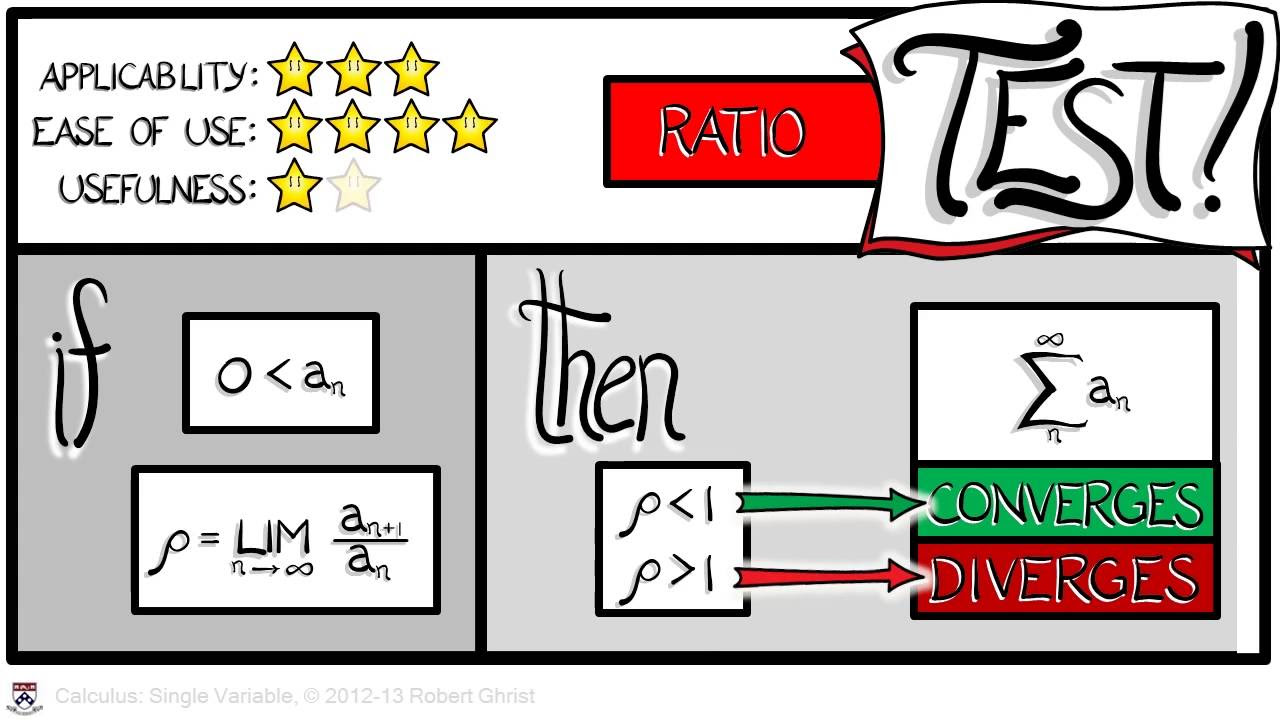
- 📈 The ratio test is ideal for series with factorial terms or terms that can be related to a geometric series, determining convergence by the limit of the ratio of successive terms.
- 🎯 The video emphasizes the importance of choosing the right test based on the characteristics of the series, rather than memorizing which test to use.
- 🏁 The script concludes with the presenter stepping away to show the full solutions for all eight series, encouraging viewers to check specific answers if needed.
Q & A
What is the main challenge students face when introduced to series?
-The main challenge students face is knowing which test to use for different kinds of series, as there are many different tests available.
What is the purpose of the video mentioned in the script?
-The purpose of the video is to help students match eight different series with the appropriate test to determine their convergence or divergence.
What is a geometric series and why is it the first series discussed in the video?
-A geometric series is a series with a fixed ratio between consecutive terms. It is discussed first because it is the simplest and was the starting point of the course on series.
How does the video approach the problem of identifying the correct test for a geometric series?
-The video identifies a geometric series by looking for a fixed ratio and then applies the geometric series test after simplifying the expression to match the standard form.
What is the interval test and when is it used in the video?
-The interval test involves examining the convergence of an improper integral of the function representing the series. In the video, it is used for a series with a negative exponential term after performing a substitution.
Why is the integral test considered a last resort in the video?
-The integral test is considered a last resort because it often requires more work, such as integration, and there are simpler methods available for many series.
What is the alternating series test and when is it applicable?
-The alternating series test is used for series with terms that alternate in sign and decrease in absolute value. It is applicable when the remaining part of the term is positive, decreasing, and has a limit of zero.
What is the divergence test and how does it work?
-The divergence test involves checking if the sequence of terms does not converge to zero. If the limit of the sequence is nonzero, the series diverges.
What is the comparison test and how does it relate to geometric and P-series?
-The comparison test involves comparing the given series to a known convergent series, such as a geometric series or a P-series, to determine if it converges. It is used when the terms of the series resemble the terms of a known convergent series.
What is the difference between the comparison test and the limit comparison test?
-The comparison test directly compares the terms of two series, while the limit comparison test compares the limit of the ratio of the terms of the two series. The limit comparison test is generally stronger and applies to a wider set of examples.
What is the root test and when should it be used?
-The root test involves taking the nth root of the absolute value of the terms and examining its limit as n approaches infinity. It should be used when the series has terms that are a 'messy' expression to the power of n.
What is the ratio test and how does it help determine the convergence of a series?
-The ratio test involves taking the limit of the ratio of consecutive terms of the series. If the limit is less than 1, the series converges; if it is greater than 1, the series diverges; if it equals 1, the test is inconclusive.
Outlines
📚 Introduction to Series Tests
This paragraph introduces the challenge students face in identifying the correct test for different types of series. The speaker outlines a plan to present eight series and match them with the appropriate convergence tests through a matching game. The video will culminate with the full answers provided without narration, allowing viewers to check specific answers at their leisure. The first series discussed is the geometric series, which requires identifying a fixed ratio. The second series mentioned has a ratio that resembles two-fifths to the power of n, but requires manipulation to fit the geometric series formula. The goal is to apply the geometric series test and determine convergence based on the common ratio.
🔍 Applying Series Convergence Tests
The speaker proceeds to apply various convergence tests to different series, starting with the interval test and integral test, which are used when a series can be represented by a function that converges. The integral test is often reserved as a last resort due to its complexity. Next, the alternating series test is discussed, which requires the series to be decreasing, positive, and have a limit of zero. The divergence test is highlighted as a quick first-check method, where if the sequence does not converge to zero, the series diverges. The paragraph concludes with a brief mention of the comparison test and limit comparison test, which are applicable when a series can be compared to a known convergent series, such as geometric or P-series.
📉 Series Tests: Comparison, Limit Comparison, Ratio, and Root
In this paragraph, the focus shifts to the comparison test and limit comparison test, which are used when a series can be compared to a simpler, known convergent series. The speaker explains that certain series are more suited to these tests based on their form, such as having terms that resemble P-series. The ratio test and root test are also introduced, with the root test being ideal for series with terms raised to the power of n. The ratio test is suggested for series with factorial terms, which are not as straightforward as geometric series but still fit the criteria for this test. The speaker emphasizes the importance of choosing the right test based on the characteristics of the series and provides a brief overview of how each test is applied.
🎉 Conclusion and Full Solution Reveal
The final paragraph of the script indicates that the speaker will step away from the screen, allowing the full solutions for all eight series to be revealed without further commentary. This gives viewers the opportunity to review the solutions at their own pace and verify the application of the various series tests discussed throughout the video. The music signifies the transition to this conclusion segment, marking the end of the instructional part of the video.
Mindmap
Keywords
💡Series
💡Geometric Series
💡Convergence
💡Test
💡Integral Test
💡Alternating Series Test
💡Divergence Test
💡Comparison Test
💡Limit Comparison Test
💡Ratio Test
💡Root Test
Highlights
Introduction to various tests for series convergence.
Eight different series are presented for a matching game.
Explanation of when to use the geometric series test, identifying a fixed ratio.
Adjusting for the geometric series formula by factoring out constants.
Discussion on the interval test and its application to series.
Use of the integral test for series with an integrable function representation.
The importance of considering the simplicity of methods before using the integral test.
Introduction of the alternating series test and its conditions.
Criteria for applying the alternating series test: decreasing terms and limit to zero.
Diverges test explained: sequence not converging to zero implies series divergence.
Comparison test and limit comparison test based on geometric and P-series.
Guidance on choosing between comparison and limit comparison tests.
Root test identification for series with terms to the power of n.
Application of the root test to determine series divergence.
Ratio test as a method of last resort for factorial terms.
Process of elimination to identify the appropriate test for each series.
Final summary of the series tests and their applications.
Music and conclusion of the video with full solutions provided.
Transcripts
Browse More Related Video

Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test

A Lot of Series Test Practice Problems

Calculus BC Unit 11 Recap

Unit 10 Study Guide - AP Calculus (BC Only)

Infinite Series Multiple Choice Practice for Calc BC (Part 5)
Calculus Chapter 5 Lecture 52 Convergence Tests 2
5.0 / 5 (0 votes)
Thanks for rating: