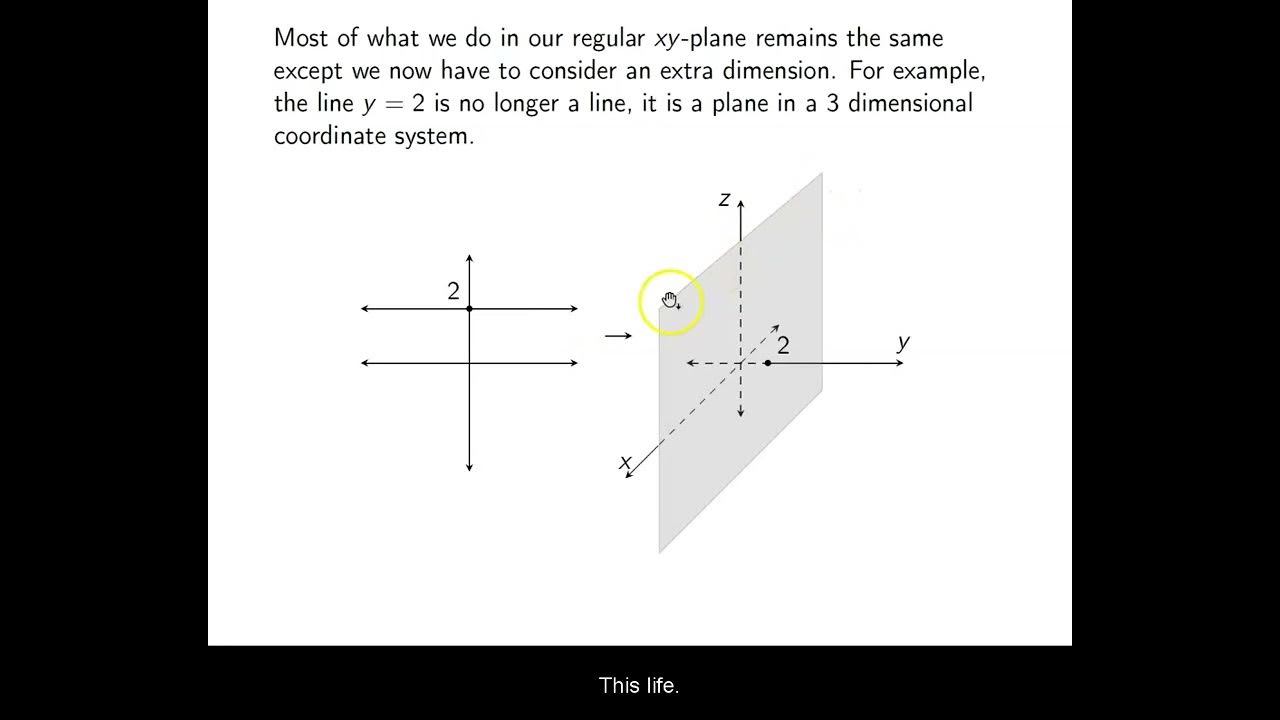
Equations for Spheres (Introduction)
TLDRThis video from Houston Math Prep introduces the concept of sphere equations in 3D space. It explains the standard definition of a sphere, its radius, and center, and demonstrates how to derive the equation of a sphere centered at the origin with a given radius. The video further explores how to find the center and radius from a given sphere equation and discusses the general center-radius form for spheres not centered at the origin. It also covers special cases, such as spheres tangent to the origin and those with antipodal points, providing a comprehensive guide to understanding and working with sphere equations in 3D.
Takeaways
- 📚 The script introduces the concept of a sphere in 3D space, defining it as a 2D surface where all points are equidistant from a single point, known as the center.
- 🔍 The standard equation for a sphere centered at the origin with radius \( r \) is \( x^2 + y^2 + z^2 = r^2 \), which is analogous to the circle equation in 2D space but includes the \( z \) term for the third dimension.
- 📐 The script demonstrates how to write the equation of a sphere with a given radius and center at the origin, such as a sphere with a radius of 3, which has the equation \( x^2 + y^2 + z^2 = 9 \).
- 🔑 It explains how to determine the center and radius of a sphere from its equation, including when the sphere's equation is given in the form \( x^2 + y^2 + z^2 = r^2 \).
- 🌐 The general center-radius form of a sphere's equation is presented, which accounts for spheres not centered at the origin by translating the center to coordinates \( (a, b, c) \).
- 📝 The script provides a method to find the center and radius of a sphere given its equation in the general form, using the example of a sphere with center coordinates \( (4, -1, 2) \) and a radius of \( 2\sqrt{5} \) units.
- 📈 It illustrates how to write the equation of a sphere given its center and radius, as well as how to interpret the formula when the center is not at the origin.
- 🔬 The concept of a sphere being tangent to the origin is discussed, where the sphere's surface intersects the origin, and the radius is the distance between the center and the origin.
- 🌡 An example is given to find the equation of a sphere with antipodal points, which are points on opposite sides of the sphere, and the center is the midpoint between these points.
- 📊 The script concludes with a mention of future videos that will cover more examples of sphere equations, including completing the square to determine the equation or find the center and radius.
- 👋 The presenter thanks the viewers and teases the next video in the series, encouraging viewers to continue learning about sphere equations.
Q & A
What is the standard definition of a sphere in 3D space?
-A sphere is a 2D surface inside 3D space where all of its points are at the same distance from a single point, which is called the center, and that distance is known as the radius.
What is the equation of a sphere centered at the origin with radius r?
-The equation of a sphere centered at the origin (0, 0, 0) with radius r is given by \( x^2 + y^2 + z^2 = r^2 \).
How do you write the equation of a sphere with a center at the origin and a radius of 3?
-The equation for a sphere with a radius of 3 and centered at the origin is \( x^2 + y^2 + z^2 = 9 \).
What does the term 'antipodal points' refer to in the context of a sphere?
-Antipodal points are points on a sphere that are located on opposite sides of the sphere, directly across from each other.
How do you find the center of a sphere given two antipodal points?
-The center of a sphere given two antipodal points is found by calculating the midpoint between the two points, which is the average of their coordinates.
What is the general center-radius form of the equation for a sphere in 3D space?
-The general center-radius form of the equation for a sphere is \( (x - a)^2 + (y - b)^2 + (z - c)^2 = r^2 \), where (a, b, c) is the center of the sphere and r is the radius.
How do you determine the radius of a sphere if the sphere is tangent to the origin?
-If a sphere is tangent to the origin, the radius of the sphere is the distance between the center of the sphere and the origin, which can be found using the distance formula in 3D space.
What is the equation of a sphere with a center at (4, -1, 2) and a radius of \( \sqrt{20} \)?
-The equation of the sphere is \( (x - 4)^2 + (y + 1)^2 + (z - 2)^2 = 20 \).
How can you find the center and radius of a sphere given its equation in the form \( (x - a)^2 + (y - b)^2 + (z - c)^2 = r^2 \)?
-The center of the sphere is given by the coordinates (a, b, c), and the radius is the square root of the right-hand side of the equation, r.
What is the relationship between the equation of a sphere in 3D space and the equation of a circle in 2D space?
-The equation of a sphere in 3D space is similar to the equation of a circle in 2D space, with the addition of the z-term to account for the third dimension, making it \( x^2 + y^2 + z^2 = r^2 \) for a sphere compared to \( x^2 + y^2 = r^2 \) for a circle.
Outlines
📚 Introduction to Sphere Equations in 3D Space
This paragraph introduces the concept of sphere equations in three-dimensional space. The speaker, Houston Math Prep, explains the standard definition of a sphere as a 2D surface in 3D space where all points are equidistant from a single point, known as the center. The distance from the center to any point on the sphere is the radius. The formula for the equation of a sphere centered at the origin is derived, which is x² + y² + z² = r², where r is the radius. The paragraph also demonstrates how to write the equation for a sphere with a given radius and how to determine the center and radius from a given equation.
🔍 General Center-Radius Form of Sphere Equations
The second paragraph delves into the general center-radius form of sphere equations, which accounts for spheres not centered at the origin. The formula (x-a)² + (y-b)² + (z-c)² = r² is introduced, where (a, b, c) represents the coordinates of the sphere's center. The paragraph explains how to identify the center and radius from this equation using two examples. The first example has a sphere with a center at (4, -1, 2) and a radius of √20, while the second example has a center at (0, 3, -5) and a radius of √(5/4).
📘 Writing Sphere Equations Given Center and Radius
This paragraph focuses on how to write the equation of a sphere when the center and radius are given. The process involves substituting the center coordinates into the general center-radius form and adjusting the signs accordingly. An example is provided where the center is at (-1/2, 0, 3/4) and the radius is 4, resulting in the equation x + 1/2)² + y² + (z - 3/4)² = 16. The paragraph also discusses a scenario where a sphere is tangent to the origin, explaining how to find the radius by using the distance between the center and the origin.
🔄 Finding Sphere Equations with Antipodal Points
The final paragraph addresses the task of finding the equation of a sphere given two antipodal points, which are points on opposite sides of the sphere. The center of the sphere is determined to be the midpoint between these points. The radius is found by calculating the distance between the center and one of the antipodal points or by finding the diameter and dividing by two. An example is given with points (6, 3, -1) and (-2, 1, -5), resulting in a center at (2, 2, -3) and a radius of √21, leading to the equation (x - 2)² + (y - 2)² + (z + 3)² = 21.
Mindmap
Keywords
💡Sphere
💡Equation
💡3D Space
💡Radius
💡Center
💡Origin
💡Distance Formula
💡Tangent
💡Apodal Points
💡Completing the Square
Highlights
Introduction to sphere equations in 3D space.
Definition of a sphere as a 2D surface in 3D space with all points equidistant from a single point, the center.
Explanation of the radius as the constant distance from the center to any point on the sphere.
Derivation of the sphere equation centered at the origin using the distance formula in 3D space.
Presentation of the standard equation for a sphere: \( x^2 + y^2 + z^2 = r^2 \).
Comparison of the sphere equation to the equation for a circle in 2D space.
Example problem: Writing the equation for a sphere with a center at the origin and a radius of 3.
Method to determine the center and radius from a given sphere equation.
General center-radius form of a sphere equation accommodating any center coordinates.
Illustration of how to find the center and radius for a sphere not centered at the origin.
Explanation of the process to write the formula for a sphere given the center and radius.
Example of finding the equation for a sphere tangent to the origin with a given center.
Calculation of the radius using the distance between the center and the origin for a tangent sphere.
Introduction of antipodal points and their significance in finding the center and radius of a sphere.
Method to find the midpoint between antipodal points to determine the sphere's center.
Technique to calculate the radius using the distance between the center and one of the antipodal points.
Writing the final equation for a sphere with a found center and radius.
Announcement of the next video in the series focusing on completing the square for sphere equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: