How to Learn Probability Distributions

Mutual Information

13 Apr 202110:54

EducationalLearning

32 Likes 10 Comments

TLDRIn this video, the host explores the most effective way to understand probability distributions by using an analogy of memorizing a complex pattern. He argues that focusing on the stories that connect various distributions, rather than their individual definitions, simplifies the learning process. The video illustrates how several distributions, including the Bernoulli, Geometric, Negative Binomial, Binomial, Exponential, Gamma, and Poisson, are related through simple counting rules and continuous analogies, providing insights that make them easier to remember and apply.

Takeaways

🧠 The video emphasizes the importance of finding simple patterns to understand complex concepts, such as probability distributions.
📈 It introduces an analogy with a complex diagram to illustrate the idea that recognizing patterns makes memorization and understanding easier.
📚 The presenter suggests focusing on the stories that relate different probability distributions rather than their individual definitions.
🔢 The script explains how different probability distributions, like Bernoulli, Geometric, Negative Binomial, Binomial, Exponential, Gamma, and Poisson, are related through simple counting rules.
🔑 It uses the concept of 'thinning' a distribution to transition from discrete to continuous distributions, providing an intuitive understanding of their parameters.
🔄 The video highlights the discrete-to-continuous analogies, such as the Exponential being the continuous version of the Geometric, and the Gamma being the continuous version of the Negative Binomial.
📊 The script discusses summation relationships between distributions, showing how summing certain distributions results in others, like the Negative Binomial being a sum of Geometric distributions.
📚 It argues that understanding these relationships provides additional properties of the distributions almost for free, without needing to memorize them individually.
🎓 The presenter shares personal stories and examples that helped demystify certain distributions, such as the Student's t-distribution, Laplace distribution, and Cauchy distribution.
🌐 The video mentions a comprehensive graph and a dedicated website that map out the relationships between various probability distributions, suggesting it as a resource for further exploration.
👍 The video concludes by encouraging viewers to learn about these relational stories as a more efficient way to understand a multitude of probability distributions.

Q & A

What is the main teaching strategy suggested by the speaker for learning about probability distributions?
-The speaker suggests learning about probability distributions by focusing on the stories that relate them rather than memorizing their individual definitions. This approach helps in understanding the patterns and relationships between different distributions.
How does the analogy of memorizing a complex pattern relate to learning probability distributions?
-The analogy illustrates that it's easier to remember a complex pattern if you understand the simple rules behind it. Similarly, understanding the underlying stories or patterns in probability distributions makes it easier to grasp their properties and relationships.
What is the Bernoulli distribution and what parameter does it have?
-The Bernoulli distribution is the simplest random variable that yields one of two outcomes. It has one parameter, the probability 'p' of one of the outcomes occurring, which in the script is given as 0.3.
How is the Geometric distribution related to the Bernoulli distribution?
-The Geometric distribution is related to the Bernoulli distribution by counting the number of trials needed to get a success (blue box), and it carries the same parameterization as the Bernoulli distribution, which is the probability 'p' of success.
What is the Negative Binomial distribution and how is it derived from the Bernoulli distribution?
-The Negative Binomial distribution is derived from the Bernoulli distribution by drawing lines over every 'r'th blue box and counting the number of yellow boxes between them. It has a parameter 'r' which equals the number of trials between successes.
How does the Binomial distribution differ from the Geometric and Negative Binomial distributions?
-The Binomial distribution differs by counting the number of successes (blue boxes) in a fixed number of trials (separated by lines every six boxes in the example), whereas the Geometric counts the number of trials to the first success and the Negative Binomial counts the number of trials between a fixed number of successes.
What is the continuous version of the Geometric distribution and how is it derived?
-The continuous version of the Geometric distribution is the Exponential distribution. It is derived by dividing the probability of a blue box by a large positive number 'c' and summing the boxes between all blue boxes, where each box now counts for 1 over 'c'.
What is the relationship between the Gamma distribution and the Negative Binomial distribution?
-The Gamma distribution can be viewed as a continuous version and a generalization of the Negative Binomial distribution. It is derived by summing up exponential distributions, analogous to summing up geometric distributions to get the Negative Binomial.
How is the Poisson distribution related to the Binomial distribution?
-The Poisson distribution is the continuous version of the Binomial distribution. It is derived by counting the number of blue boxes between blocks that sum to a fixed number, in this case, six.
What are some additional insights provided by the speaker regarding the relationships between different distributions?
-The speaker provides insights such as the discrete-to-continuous analogies (e.g., Exponential to Geometric), summation relationships (e.g., summing Geometric distributions results in a Negative Binomial), and how certain distributions can be derived from others through specific processes, like the Student's t-distribution from a specific process involving a Gamma distribution and a Normal distribution.
What is the purpose of the large graph mentioned at the end of the script?
-The large graph is a comprehensive visual representation that shows the relationships between various probability distributions. It is meant to be a starting point for those who wish to explore the connections between distributions in more depth.

Outlines

00:00

🧠 Mastering Probability Distributions Through Analogies

The video introduces a unique approach to understanding probability distributions by using an analogy of memorizing a complex pattern within a minute. The presenter, DJ, suggests that recognizing patterns simplifies the learning process. The analogy is extended to probability distributions, where focusing on the stories that connect them, rather than individual definitions, is advocated. The video aims to show that by understanding the relationships between different distributions, one can grasp a vast amount of information with less effort. The summary of this paragraph emphasizes the importance of finding simple patterns to explain complexity in learning probability distributions.

05:00

📚 The Storytelling Method for Probability Distributions

This paragraph delves into the storytelling method by using the Bernoulli distribution as a starting point and explaining how different criteria for counting can lead to various distributions such as geometric, negative binomial, binomial, exponential, gamma, and Poisson. The presenter illustrates how these distributions are interconnected and how understanding their relationships can provide insights into their properties. The summary highlights the discrete-to-continuous analogies, the concept of summation relationships, and how these connections can help in memorizing and understanding the distributions without needing to memorize individual properties.

10:00

🔍 Exploring Advanced Relationships and Insights

The final paragraph discusses advanced relationships between different probability distributions, providing examples that demystify certain distributions like the Student's t, Laplace, and Cauchy. It explains how these distributions can be derived from simpler ones through processes like sampling and transformation. The presenter also mentions a comprehensive graph that visually represents the relationships between various distributions, which is a valuable resource for further exploration. The summary emphasizes the value of these stories in providing additional properties and insights, helping to solidify the understanding of probability distributions.

Mindmap

Keywords

💡Probability Distributions

Probability distributions are a fundamental concept in statistics that describe the likelihood of different possible outcomes in an experiment. In the video, the focus is on understanding various probability distributions by learning the stories that relate them, which simplifies the process of memorization and comprehension. The script uses the analogy of complex patterns to explain how recognizing underlying relationships can make learning these distributions more manageable.

💡Analogy

An analogy is a comparison between two things for the purpose of explanation or clarification. In the context of the video, the presenter uses an analogy of memorizing a complex pattern to illustrate the importance of finding simple patterns or rules that can explain complex phenomena, such as probability distributions. This method aids in better understanding and memorization of the material.

💡Bernoulli Distribution

The Bernoulli distribution is a discrete probability distribution for a random variable that takes on one of two possible outcomes, often represented as success (e.g., 'blue box') and failure (e.g., 'yellow box'). In the video, the Bernoulli distribution is used as a starting point to explain how different probability distributions are related through a series of counting criteria.

💡Geometric Distribution

The geometric distribution is used to model the number of trials required for a success in a series of Bernoulli trials. In the video, it is related to the Bernoulli distribution by counting the number of 'yellow boxes' between 'blue boxes', and it carries the same parameterization, which is the probability of a 'blue box'.

💡Negative Binomial Distribution

The negative binomial distribution is concerned with the number of failures before a fixed number of successes occur in Bernoulli trials. The video script explains it by drawing lines over every other 'blue box' and counting the 'yellow boxes' in between, with the 'r' parameter equal to two, indicating two failures before the next success.

💡Binomial Distribution

The binomial distribution is a discrete probability distribution for the number of successes in a fixed number of independent Bernoulli trials with the same probability of success. In the video, it is introduced by counting 'blue boxes' between groups of six boxes, with the 'n' parameter set to six.

💡Continuous Distribution

Continuous distributions are used when the random variable can take on any value within an interval. The video discusses the transition from discrete to continuous distributions by dividing the probability of a 'blue box' by a large number and considering the limit as this number approaches infinity, leading to distributions like the exponential and gamma.

💡Exponential Distribution

The exponential distribution is a continuous probability distribution that models the time between events in a Poisson process. In the video, it is described as the continuous version of the geometric distribution, where the rate parameter is the probability of a 'blue box'.

💡Gamma Distribution

The gamma distribution is a two-parameter family of continuous probability distributions. The video script explains it as a continuous version and generalization of the negative binomial distribution, with shape and scale parameters that relate to the counting criteria used in the discrete case.

💡Poisson Distribution

The Poisson distribution is used to model the number of events occurring in a fixed interval of time or space, given a constant average rate of occurrence. In the video, it is introduced as a distribution that counts 'blue boxes' between each block that sums to six, with a rate parameter equal to six times the probability of a 'blue box'.

💡Central Limit Theorem

The central limit theorem is a statistical theory that states that the distribution of sample means approximates a normal distribution as the sample size gets larger, regardless of the shape of the population distribution. The video hints at this theorem as a pattern that can be used to understand why certain distributions approach the normal distribution under certain conditions.

💡Student's t-distribution

Student's t-distribution is a type of continuous probability distribution that arises when estimating the mean of a normally distributed population, especially when the sample size is small. The video script provides a story that relates the gamma distribution to the Student's t-distribution, helping to demystify the latter by showing it as a mixture of normal distributions with varying variances.

💡Laplace Distribution

The Laplace distribution is a continuous probability distribution that is used in various fields, including machine learning for generating sparse solutions. The video script explains it through the difference of two samples from an exponential distribution, providing an intuitive understanding of the distribution by relating it to a familiar context.

💡Cauchy Distribution

The Cauchy distribution is a continuous probability distribution that is notable for having an undefined mean and variance. The video script demystifies this distribution by showing it as a ratio of two standard normal variables, where the denominator has an expected value of zero, thus providing a clearer understanding of its properties.

Highlights

The video introduces an analogy to explain the complexity of memorizing details versus understanding patterns.

The importance of finding simple patterns to explain complexity in learning about probability distributions.

The suggestion to focus on stories that relate probability distributions rather than their individual definitions.

An explanation of the Bernoulli distribution as the simplest random variable with two outcomes.

The geometric distribution is derived from the Bernoulli distribution by counting the number of trials until the first success.

The negative binomial distribution is introduced as a generalization of the geometric distribution with varying criteria for success.

The binomial distribution is explained as a result of grouping boxes and counting successes within those groups.

A method to create continuous versions of discrete distributions by dividing the probability of success by a large number.

The exponential distribution is presented as the continuous analog of the geometric distribution.

The gamma distribution is shown as a continuous generalization of the negative binomial distribution.

The Poisson distribution is explained as a continuous version of the binomial distribution, counting occurrences in fixed intervals.

The concept of discrete to continuous analogies is highlighted to aid in understanding complex distributions.

Summation relationships between distributions, such as the sum of geometric distributions leading to the negative binomial.

An introduction to the gamma distribution as a sum of exponential distributions.

The central limit theorem is mentioned as a reason distributions approach the normal distribution under certain conditions.

Additional stories are provided to demonstrate the range of relationships between different probability distributions.

The video concludes by emphasizing the value of learning stories that relate distributions for better understanding and memorization.

A call to action for viewers to like, subscribe, and support the content for continued learning about statistics and machine learning.

Transcripts

Browse More Related Video

Introduction to Probability Distributions

Probability: Types of Distributions

Types Of Distribution In Statistics | Probability Distribution Explained | Statistics | Simplilearn

Basics of Probability, Binomial and Poisson Distribution

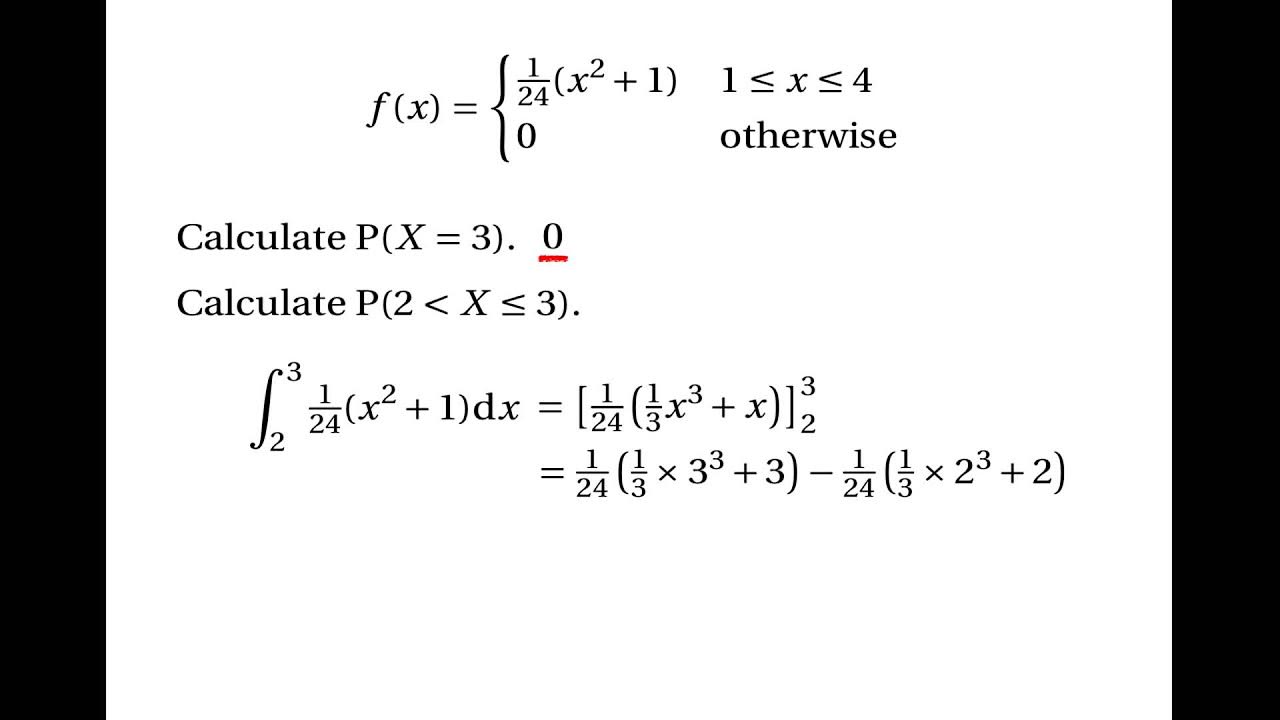
Continuous Random Variables: Probability Density Functions

Probability Distributions Made Easy: Top 3 to Know for Data Science Interviews