4.2.6 Addition and Multiplication Rules - The Principle of Redundancy and the Multiplication Rule

Sasha Townsend - Tulsa
9 Oct 202011:55
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explores the principle of redundancy, emphasizing its importance in enhancing system reliability. It illustrates redundancy with everyday examples like human eyes and applies it to engineering scenarios, such as aerospace and computer data backup. The script explains how the multiplication rule in probability theory supports redundancy, showing that the likelihood of multiple independent failures is significantly reduced, thus ensuring data safety and system performance. It concludes by summarizing the addition and multiplication rules in probability, which are key to understanding redundancy's impact on reliability.

Takeaways
  • 📚 The Principle of Redundancy: The concept involves incorporating multiple components to serve the same purpose, ensuring the system continues to function even if one component fails.
  • 🛠️ Design Application: The principle is applied in design to increase reliability, such as in aerospace engineering where multiple engines are used to ensure the plane can still fly if one engine fails.
  • 👀 Biological Example: Humans have two eyes as an example of passive redundancy, allowing us to see even if one eye has a problem.
  • 💾 Data Backup: The importance of backing up computer data is highlighted, using the multiplication rule to calculate the probability of failure with multiple backups.
  • 📉 Probability Calculation: The script explains how the probability of disk drive failure decreases exponentially with the addition of each backup, illustrating the effectiveness of redundancy.
  • 🔢 Multiplication Rule: The rule is used to calculate the probability of multiple independent events (like disk drive failures) occurring together, which is the basis for understanding redundancy's impact on reliability.
  • 📉 Decreasing Failure Rates: With each additional backup, the combined probability of all backups failing simultaneously becomes significantly smaller, enhancing data security.
  • 🤔 Importance of Backups: The script challenges the notion that having a single copy of data is sufficient, emphasizing the benefits of multiple backups to prevent data loss.
  • 📈 Reliability Increase: The principle of redundancy significantly increases the reliability of a system by reducing the likelihood of simultaneous component failures.
  • ⚠️ Addition and Multiplication Rules: The script concludes with a summary of the addition and multiplication rules in probability, which are key to understanding the principle of redundancy.
Q & A

  • What is the principle of redundancy?

    -The principle of redundancy involves including multiple components that serve the same purpose so that if one component fails, the entire system still functions as intended.

  • How does redundancy relate to reliability?

    -Redundancy increases the reliability of a system by ensuring that backup components can take over if one component fails, reducing the likelihood of complete system failure.

  • Can you provide an example of passive redundancy?

    -Yes, an example of passive redundancy is having two eyes. If one eye has a problem, the other eye can still function, ensuring that you can see.

  • How is redundancy applied in aerospace engineering?

    -In aerospace engineering, redundancy is applied by having more than one engine on an airplane. If one engine fails, the other engine(s) can keep the plane operational.

  • What is the probability of a single disk drive failing in a year according to the given example?

    -The probability of a single disk drive failing in a year is 3%, or 0.03 in decimal form.

  • How do you calculate the probability of both a primary and a backup disk drive failing?

    -You use the multiplication rule by multiplying the probability of the primary disk drive failing by the probability of the backup disk drive failing. Since these are independent events, the calculation is 0.03 * 0.03 = 0.0009 or 0.09%.

  • What is the probability that all three disk drives will fail?

    -The probability that all three disk drives will fail is calculated by multiplying the failure probabilities of each drive: 0.03 * 0.03 * 0.03 = 0.000027, which is 0.0027%.

  • Why is backing up computer data not considered wasteful?

    -Backing up computer data is not considered wasteful because it significantly reduces the probability of losing all data due to multiple failures, adhering to the principle of redundancy.

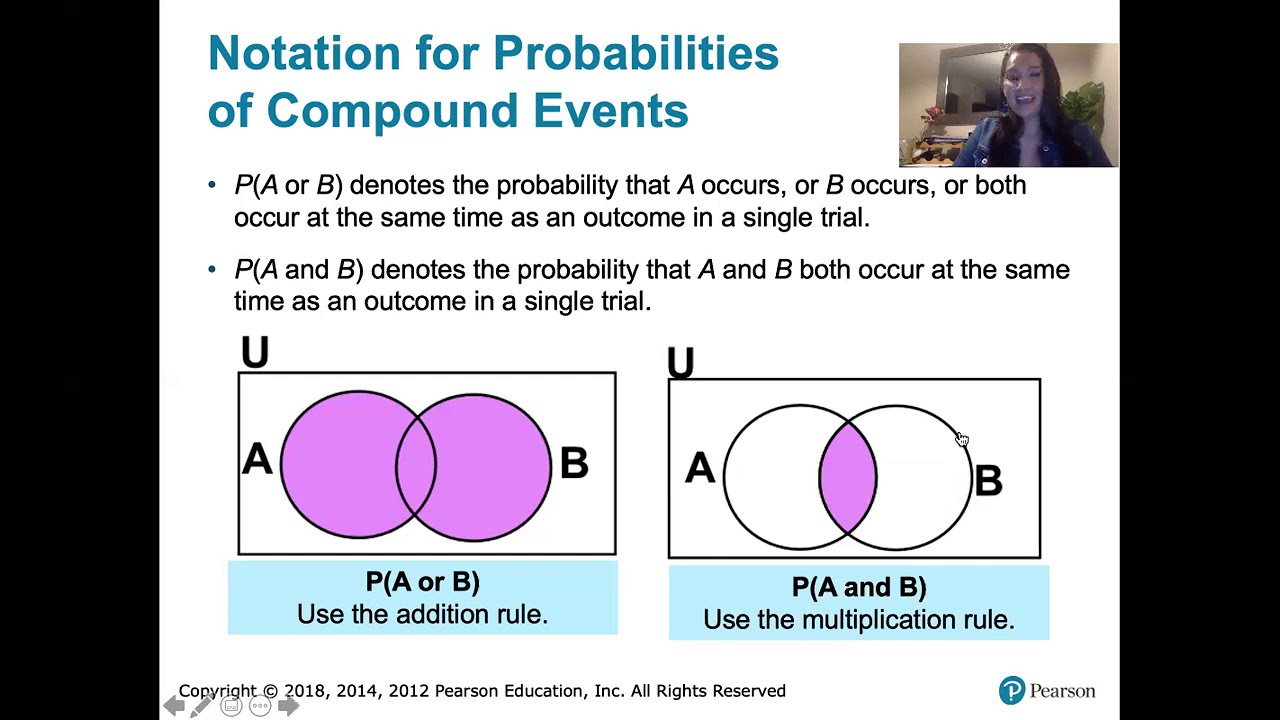
  • What does the addition rule state?

    -The addition rule states that if you want to find the probability that event A or event B (or both) occur, you add the probabilities of A and B occurring, ensuring that any overlap is only counted once.

  • When should you use the multiplication rule in probability?

    -You should use the multiplication rule when you need to find the probability that event A and event B both occur. This involves multiplying the probability of A by the probability of B, considering any dependencies between events.

  • What are independent events in the context of the multiplication rule?

    -Independent events are those where the occurrence of one event does not affect the probability of the other event occurring. In this case, the multiplication rule is applied directly by multiplying their probabilities.

  • How are dependent events handled in the multiplication rule?

    -For dependent events, the probability of the second event is adjusted based on the occurrence of the first event. You calculate the probability of the first event, then multiply it by the conditional probability of the second event given that the first event has occurred.

Outlines
00:00
🔒 The Principle of Redundancy for Reliability

This paragraph introduces the principle of redundancy, which is a fundamental concept in system design to enhance reliability. The principle involves incorporating multiple components that serve the same function, ensuring the system continues to operate even if one component fails. The video script uses the human eyes as an example of passive redundancy and discusses its application in aerospace engineering, where multiple engines in an airplane serve as backups for each other. The script also addresses the importance of data backup on computer hard drives to prevent data loss, illustrating the concept with a problem involving the probability of disk drive failure.

05:03
📚 Applying the Multiplication Rule to Redundancy

The second paragraph delves into the application of the multiplication rule in calculating the probability of failure in systems with redundancy. It explains how the probability of failure decreases significantly when multiple independent backup systems are in place. The script provides a detailed example of how the probability of losing data from a computer with a single hard drive is reduced by backing up data on a second drive, and further reduced with a third backup. The multiplication rule is used to calculate the probabilities of concurrent failures of the drives, demonstrating the effectiveness of redundancy in minimizing the risk of total system failure.

10:04
📘 Summarizing the Addition and Multiplication Rules in Probability

The final paragraph summarizes the two key rules of probability discussed in the video script: the addition rule and the multiplication rule. The addition rule is explained as a method to find the probability of either one event or another occurring, ensuring outcomes are not double-counted. The multiplication rule is described for calculating the probability of two events occurring consecutively, with an emphasis on the importance of adjusting the probability of the second event if the first has already occurred, indicating the dependency between events. The paragraph concludes with a reminder of the significance of these rules in understanding and applying the concept of redundancy to enhance system reliability.

Mindmap
Keywords
💡Redundancy
Redundancy in the context of the video refers to the inclusion of multiple components serving the same purpose to ensure that if one fails, the system continues to operate as intended. It is a principle used in system design to increase reliability. The video illustrates this with the example of having two eyes, where the failure of one does not impede vision, thus providing a natural form of redundancy.
💡Reliability
Reliability is the measure of the dependability of a system to perform its intended function over time. In the video, it is shown that incorporating redundancy can significantly enhance the reliability of a system, such as using multiple engines in an airplane or having multiple copies of data to prevent loss.
💡Multiplication Rule
The multiplication rule is a probabilistic principle used to calculate the likelihood of multiple independent events occurring together. In the video, it is applied to determine the probability of multiple hard drives failing simultaneously, demonstrating how redundancy decreases the overall risk of system failure.
💡Backup
Backup refers to the process of making additional copies of data to prevent loss in case the original data becomes unavailable. The video emphasizes the importance of backups in the context of the multiplication rule, showing that having multiple backups drastically reduces the probability of data loss.
💡Failure Rate
Failure rate is the frequency at which a system or component is expected to fail. The video uses a 3% annual hard drive failure rate as a basis for calculations, highlighting how redundancy can reduce this rate when considering multiple drives.
💡Addition Rule
The addition rule in probability is used to calculate the likelihood of one event or another occurring. The video contrasts this with the multiplication rule, explaining that the addition rule is used when considering the probability of either one event or another happening, but not both simultaneously.
💡Sample Space
Sample space is the set of all possible outcomes of an experiment. The video relates the sample space to the multiplication rule, explaining that the rule is used to find the probability of multiple events when considering the sample spaces for each individual event.
💡Independent Events
Independent events are those where the occurrence of one event does not affect the probability of the occurrence of another. The video clarifies that when using the multiplication rule, if events are independent, the probability of one event does not need to be adjusted based on the occurrence of another.
💡Dependent Events
Dependent events are events where the occurrence of one affects the probability of the other. In the video, it is mentioned that if events are dependent, the probability of one event occurring may need to be adjusted after the occurrence of another, which is an important consideration when applying the multiplication rule.
💡Aerospace Engineering
Aerospace engineering is the field that designs and builds aircraft and spacecraft. The video uses aerospace as an example of an industry where redundancy is critical, such as having multiple engines in an airplane to ensure that if one fails, the plane can still function.
💡Data Loss
Data loss refers to the accidental or intentional deletion or corruption of data. The video discusses the risk of data loss and how creating backups is a practical application of the redundancy principle to mitigate this risk, thereby increasing the reliability of data storage.
Highlights

Principle of redundancy: Include multiple components that serve the same purpose to ensure system reliability.

Example of redundancy with human eyes: If one eye fails, the other eye compensates, demonstrating passive redundancy.

Aerospace engineering uses redundancy: Multiple engines on an airplane ensure it can still operate if one engine fails.

Computer data backup: Having multiple backups reduces the probability of total data loss.

Disk drive failure rate: A 3% annual failure rate for a single disk drive.

Calculating failure probability for single and multiple drives: Using the multiplication rule to determine the likelihood of simultaneous failures.

Probability of single drive failure: 0.03 or 3%.

Probability of two drives failing: 0.0009 or 0.09%, demonstrating significant reliability improvement with a backup.

Probability of three drives failing: 0.000027 or 0.0027%, illustrating even greater reliability with multiple backups.

Summary of redundancy principle: Ensures system reliability by using backups to prevent total failure.

Addition rule for probability: Used when calculating the probability of either event A or event B occurring.

Multiplication rule for probability: Used when calculating the probability of both event A and event B occurring simultaneously.

Independent events: When the occurrence of one event does not affect the probability of another event.

Dependent events: When the occurrence of one event affects the probability of another event.

Importance of backups: Having multiple backups significantly reduces the risk of complete data loss.

Transcripts

Browse More Related Video

Chapter 4 Probability Part 2

Multiplication & Addition Rule - Probability - Mutually Exclusive & Independent Events

Math 119 Chapter 4 part 2

AP Stats Test Quick Review: Probability

Lecture 3: Birthday Problem, Properties of Probability | Statistics 110

4.2.1 Addition and Multiplication Rules - Simple and Compound Events, and Their Probabilities

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Redundancy PrincipleSystem ReliabilityProbability CalculationsMultiplication RuleEngineeringBackup StrategiesData ProtectionAerospace ExamplesLearning OutcomesEducational Video