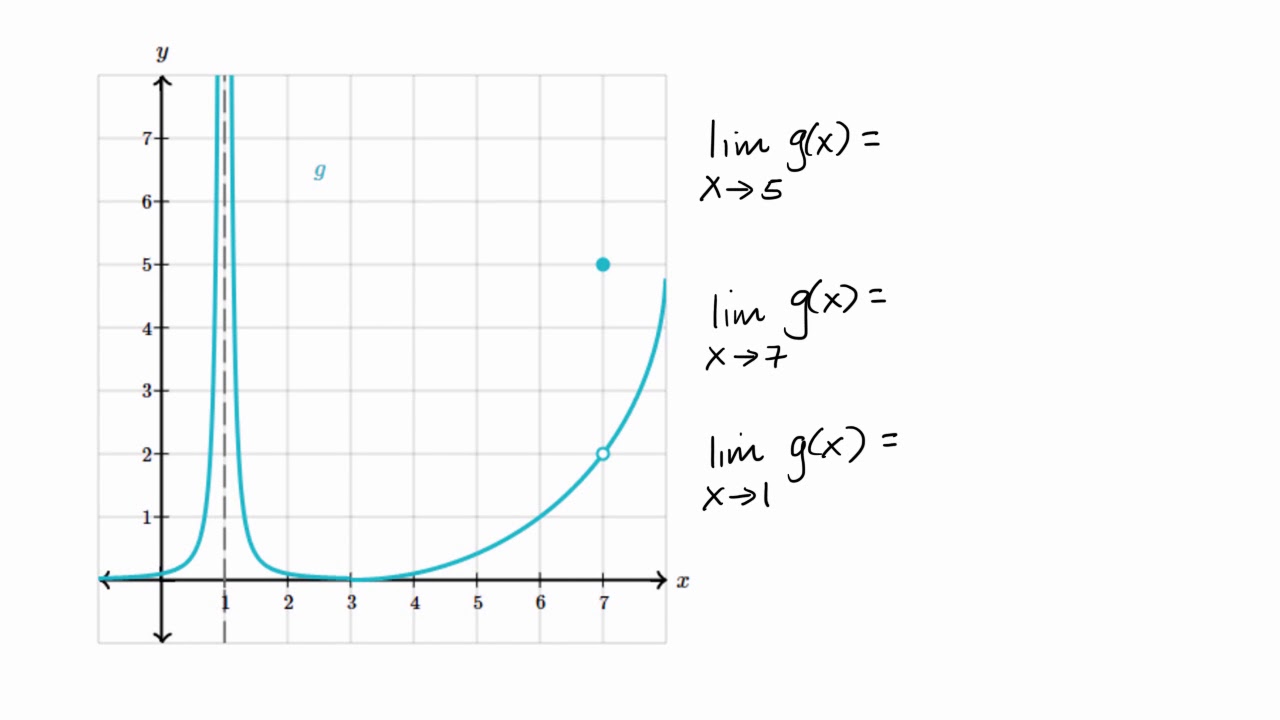
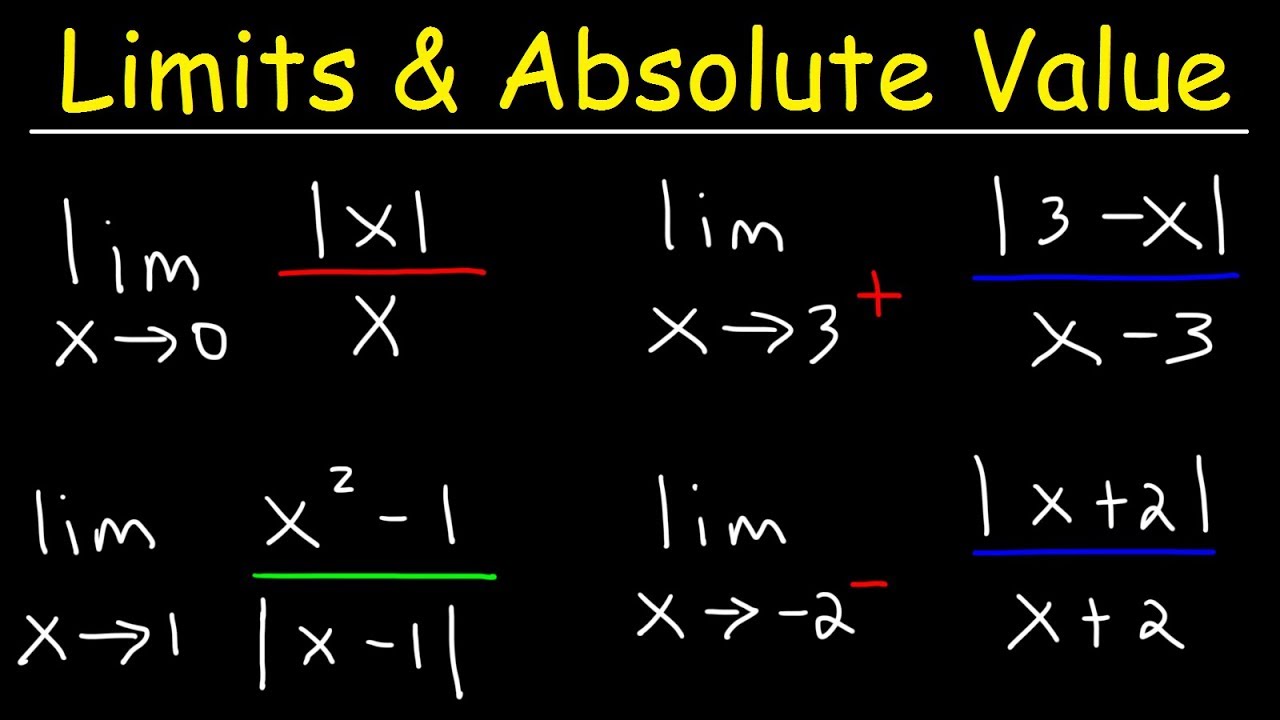Challenging Limits from Graphs
TLDRThis video script is a comprehensive walkthrough of challenging limit problems involving graphs, one-sided limits, and compositions. The presenter emphasizes the importance of understanding the behavior of the inner function as x approaches a certain value and then using that information to analyze the outer function. The script covers a variety of limit scenarios, including those involving infinity, where the limit from the left and right must match to confirm the overall limit. It also touches on the use of L'Hôpital's rule for indeterminate forms like 0/0 or ∞/∞. The presenter uses a combination of algebraic manipulation and graphical analysis to solve the problems, providing a clear and methodical approach to a topic that often intimidates students. The script is both educational and reassuring, showing that with the right techniques, even complex limit problems can be manageable.
Takeaways
- 📌 The concept of a limit as x approaches c of f(x) being equal to l implies that the left and right limits at c must also equal l.
- 📈 When dealing with compositions, such as lim (x->5) f(f(x)), first evaluate the inner function as x approaches the point of interest, then use that result to find the outer function's behavior.
- 🤔 Students often incorrectly assume that limits do not exist without properly evaluating the function's behavior from both the left and right.
- 📉 For limits involving infinity, it's important to determine whether the function approaches positive or negative infinity as x approaches the value in question.
- 🔄 The process of evaluating limits can often be simplified by using substitution, treating the inner function as a new variable u.
- 📋 It's crucial to consider the behavior of both the inner and outer functions separately when dealing with compositions.
- 🤓 The approach of x from the left or right dictates whether we consider the function's behavior from above or below, respectively.
- 🧮 When evaluating limits of products or sums, the individual limits must exist and be finite to apply arithmetic operations.
- 🚫 If a limit results in an indeterminate form like 0/0 or ∞/∞, techniques like L'Hôpital's rule may be necessary to find the limit.
- 📊 Graphs are a powerful tool for visualizing the behavior of functions and can help in determining limits without explicit algebraic manipulation.
- ✅ Always verify that the limit exists and is the same from both the left and right to ensure the limit as a whole exists at the given point.
Q & A
What are the two conditions that must be true for the limit as x approaches c of f(x) to be equal to l?
-The two conditions are: 1) The limit as x approaches c from the left of f(x) exists and is equal to l, and 2) The limit as x approaches c from the right of f(x) exists and is equal to l.
What is the concept of a 'u-substitution' in the context of evaluating limits?
-The concept of 'u-substitution' is used when dealing with composite functions. It involves setting u equal to the inner function, evaluating the limit as x approaches a certain value, and then using that result to find the limit of the outer function.
How does one determine the limit as x approaches a certain value from the left?
-To determine the limit from the left, one would look at the behavior of the function as x values just to the left of the point of interest approach that point. This is typically visualized on a number line or graph, considering the y-values that the function approaches from below.
What is the significance of evaluating the limit from both the left and the right when dealing with functions that are not continuous?
-Evaluating the limit from both the left and the right is significant because it allows one to determine whether the function has a limit at a certain point, even if the function is not continuous there. If the values from the left and right are the same, the limit exists; if they differ, the limit does not exist at that point.
How does the speaker handle the case where the limit results in infinity?
-When the limit results in infinity, the speaker reframes the problem by considering the behavior of the function as u (the result of the inner function) approaches infinity. The limit is then evaluated based on the behavior of the outer function at infinity.
What is the process for evaluating the limit of a composition of functions as x approaches a certain value?
-The process involves first determining the behavior of the inner function as x approaches the value of interest. Then, using the result of the inner function as a new variable (u), the limit is evaluated for the outer function as this new variable approaches its corresponding value.
How does the speaker approach the evaluation of limits involving sums and products of functions?
-The speaker evaluates the limits of the individual functions that make up the sum or product. For sums, the limit of the sum is the sum of the individual limits. For products, the limit is found by multiplying the individual limits, provided both limits exist and are finite.
What is the strategy for evaluating limits of rational functions or fractions?
-For rational functions, the strategy involves evaluating the limits of the numerator and the denominator separately. If both limits exist, the limit of the fraction is the ratio of those limits. If the result is 'zero over zero' or 'infinity over infinity', L'Hôpital's rule is applied by taking the derivatives of the numerator and the denominator and re-evaluating the limit.
null
-null
Why is it important to consider the behavior of a function as it approaches a certain value from above and below?
-Considering the behavior from above and below is important because it helps determine whether the function approaches a value from the right (above) or from the left (below). This distinction is crucial for establishing one-sided limits and understanding the behavior of the function at discontinuities or asymptotes.
How does the speaker use graphs to illustrate the process of evaluating limits?
-The speaker uses graphs to visually demonstrate the behavior of functions as x approaches certain values. By showing the function's graph and highlighting the approach to the value of interest, the speaker can illustrate whether the limit exists, is infinite, or does not exist, and from which direction the function approaches the given value.
What is the role of the number line in understanding limits from the left and right?
-The number line is used to conceptualize the approach to a point from different directions. Approaching a point from the left on the number line corresponds to approaching the point with decreasing values of x, while approaching from the right corresponds to increasing values of x. This helps in visualizing one-sided limits.
How does the concept of a vertical asymptote affect the evaluation of limits?
-A vertical asymptote indicates a value of x towards which the function's y-values may approach infinity or negative infinity. When evaluating limits near a vertical asymptote, it's important to consider whether the function approaches the asymptote from the left or right, as this can affect the existence and value of the limit.
What is the speaker's approach to providing a clear and comprehensive explanation of limits?
-The speaker's approach involves a step-by-step explanation, using both algebraic and graphical methods to illustrate the process. The speaker emphasizes the importance of considering one-sided limits, using the number line to visualize approaches from different directions, and applying L'Hôpital's rule when appropriate. The speaker also provides practice problems to reinforce the concepts.
Outlines
📈 Understanding Limits with Graphs and One-Sided Limits
The video introduces challenging limit problems that require understanding graphs, one-sided limits, and compositions. It emphasizes the importance of recognizing that if the limit as x approaches c of f(x) is l, then both the left and right limits must equal l. The video uses a substitution method (u = f(x)) to evaluate composite functions and stresses the need to analyze the inner function first before rewriting the limit in terms of the outer function. The process is demonstrated through examples, including analyzing the behavior of functions as they approach specific values from the left and right.
🔍 Analyzing Limits from Left and Right for Composite Functions
This paragraph delves into the process of evaluating the limits of composite functions as x approaches a certain value, focusing on both the left and right approaches. It illustrates how to rewrite the original limit in terms of an inner function (u) and then evaluate the limit based on the behavior of g(u) and f(u) on the respective graphs. The concept of approaching a value 'from below' or 'from above' is clarified in relation to 'from the left' or 'from the right,' which is crucial for determining the correct limit values.
🤝 Tackling Products and Sums of Functions in Limits
The video script explains how to find limits of products and sums of functions as x approaches a specific value. It demonstrates that for products, both left and right limits must exist, and for sums, the individual limits are added together if they are finite. The process involves evaluating f(x) and g(x) independently and then combining the results to find the overall limit. The importance of showing work and understanding the approach from both directions is highlighted.
🧠 Solving Composition Functions and Their Limits
The paragraph focuses on solving composition functions, emphasizing the strategy of first determining the behavior of the inner function and then using that information to rewrite and solve the original limit. It also covers the evaluation of limits from both the left and right, ensuring that the same result is obtained for the limit to exist. The video script provides a step-by-step guide on how to approach these problems and what to consider when rewriting limits in terms of new variables (u).
🔢 Limits of Functions with Addition and Multiplication
This section of the video script deals with finding limits of functions that involve addition and multiplication as x approaches a specific value. It shows how to individually find the limits of g(x) and f(x) + 1, and then combine these to find the overall limit. The process is demonstrated for both left and right approaches, and it is shown that if the results match, the limit exists. The video also touches upon the concept of dealing with zero times any function and the implications for the limit.
🔄 Applying L'Hôpital's Rule for Indeterminate Forms
The final paragraph addresses the scenario where the direct substitution results in an indeterminate form, such as 0/0. In these cases, L'Hôpital's rule is applied, which involves taking the derivative of the numerator and the denominator and re-evaluating the limit. The video script provides an example where the limits of g(x) and a related function are found, leading to an indeterminate form. It then demonstrates the application of L'Hôpital's rule by finding the derivatives and solving for the new limit, resulting in a definitive answer.
Mindmap
Keywords
💡limit
💡one-sided limit
💡composition of functions
💡graph analysis
💡infinity
💡asymptote
💡approach from the left/right
💡substitution
💡horizontal line test
💡continuity
Highlights
The video focuses on challenging limits, particularly those involving graphs, one-sided limits, and compositions.
To understand limits, it's essential to recognize that the limit as x approaches c of f(x) is equal to l implies two conditions: the left and right limits must both exist and be equal to l.
The concept of approaching a point from the left or right on a number line is crucial for one-sided limits.
The video utilizes a u-substitution technique to handle compositions, like f(f(x)) as x approaches a certain value.
When dealing with compositions, first determine the behavior of the inner function as x approaches the point of interest, then rewrite and solve the limit.
The video provides a methodical approach to evaluate the limit of composite functions by breaking them down into more manageable parts.
Generic graphs are used to demonstrate the process, and a PDF version is offered for viewers to practice similar analyses.
The process of finding limits involves looking at the behavior of functions as they approach certain values from both the left and right.
The video emphasizes that the limit of a composition of functions can be found by first examining the inner function and then the outer function.
For products and sums of functions, the limits are evaluated by considering each function independently and then combining the results.
The video demonstrates that the limit of a ratio of functions can be more complex, potentially requiring the use of L'Hôpital's rule for indeterminate forms.
L'Hôpital's rule is introduced as a method to solve limits of ratios when direct substitution results in an indeterminate form like 0/0 or ∞/∞.
The importance of the chain rule in calculating derivatives, especially in the context of L'Hôpital's rule, is highlighted.
The video provides a detailed walkthrough of several limit problems, emphasizing the need to approach the problem from both the left and right where applicable.
The process of evaluating limits is shown to be iterative, requiring multiple steps and the use of various mathematical concepts and rules.
The video concludes with a reminder that practice is key to understanding and solving complex limit problems.
The speaker provides encouragement and a wish for good luck to the viewers, emphasizing the value of persistence in mathematical problem-solving.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: