Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
TLDRThis video delves into the concept of limits in mathematics, bridging the intuitive understanding of approaching values with the formal epsilon-delta definition. It demonstrates how limits underpin the formal definition of derivatives, moving from the idea of infinitesimally small changes to a rigorous analysis of function behavior as inputs approach certain values. The narrative then explores L'Hopital's Rule, a method for computing limits of indeterminate forms, illustrating its application with examples and tracing its historical origins. Finally, the video prepares viewers for upcoming discussions on integrals and the fundamental theorem of calculus, emphasizing the role of limits in providing clarity to concepts flirting with infinity.
Takeaways
- 📚 The concept of a limit is foundational in calculus, essentially involving the idea of values approaching each other without necessarily reaching a precise point.
- 📈 A derivative represents the ratio of the change in the function's output to the change in its input, and this concept hinges on the principle of limits as the input change approaches zero.
- ✏️ The formal definition of a derivative aligns with intuitive understanding, using limits to describe the 'nudge' approach to zero, reinforcing the connection between theoretical math and intuitive concepts.
- 🤖 The epsilon-delta definition of limits provides a rigorous mathematical way to define the idea of one value approaching another, aiming to eliminate ambiguity in the concept of limits.
- ⚡ L'Hopital's Rule is a practical method for computing limits that appear indeterminate, like 0/0, by taking the derivatives of the numerator and denominator.
- 🖥 The notion of dx and df as finite, non-zero changes underpins a more intuitive and concrete understanding of calculus, moving away from the abstract idea of infinitesimals.
- 📝 Limits allow for the formal definition of derivatives without invoking the problematic concept of infinitely small changes, sidestepping potential paradoxes.
- 🚩 The epsilon-delta definition of limits formalizes the process of determining how function outputs converge around a particular input, providing a foundation for rigorous analysis in calculus.
- 🏆 Understanding the concept of limits is crucial before diving into integrals, serving as a bridge between the two fundamental concepts of calculus.
- 📡 The video underscores the importance of building strong intuitions in calculus, demonstrating how formal definitions and practical tricks like L'Hopital's Rule stem from these basic understandings.
Q & A
What is the main idea behind the concept of a derivative?
-The main idea behind the concept of a derivative is to find the rate of change of a function at a specific point. It involves taking a small nudge or change (dx) in the input and observing the resulting change (df) in the output, and then finding what this ratio (df/dx) approaches as the nudge size (dx) approaches zero.
How does the formal definition of a derivative relate to the intuitive understanding of the term 'approach'?
-The formal definition of a derivative uses the concept of 'approach' to describe the behavior of the ratio (df/dx) as the change in the input (dx) gets infinitely small, approaching zero. This aligns with the intuitive understanding of 'approach' as getting closer and closer to a certain value.
What is the epsilon-delta definition of limits?
-The epsilon-delta definition of limits is a rigorous way to define the concept of 'approach' in mathematics. It states that for any given distance (epsilon) however small, there exists a corresponding distance (delta) around the limiting point such that any input within delta will produce an output within epsilon of the limiting value.
Why is the epsilon-delta definition important in calculus?
-The epsilon-delta definition is important in calculus because it provides a precise and rigorous foundation for the intuitive ideas of the subject, such as limits and derivatives, by avoiding the paradoxical notion of infinitely small changes.
What is L'Hopital's Rule and how is it used?
-L'Hopital's Rule is a method for computing limits when the direct substitution leads to an indeterminate form, such as 0/0. It states that if the limit of the ratio of two functions exists, then the limit of the ratio is equal to the limit of the ratio of their derivatives, provided the limit of the denominator's derivative is not zero.
How does L'Hopital's Rule help in understanding the behavior of functions near undefined points?
-L'Hopital's Rule helps in understanding the behavior of functions near undefined points by allowing us to find the limit of a ratio even when the direct substitution results in an undefined form. It provides a systematic way to approximate the behavior of the function around the point where the function is not defined.
What is the significance of the chain rule in the context of the derivative?
-The chain rule is significant in the context of the derivative because it allows us to find the derivative of a composite function. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function evaluated at the inner function's value.
How does the concept of limits tie into the fundamental theorem of calculus?
-The concept of limits is crucial to the fundamental theorem of calculus because it provides a clear meaning to the idea of the accumulation of infinitely small changes, which is essential for understanding the relationship between differentiation and integration.
Why is it important to avoid the idea of infinitely small changes when defining derivatives?
-It is important to avoid the idea of infinitely small changes when defining derivatives because it prevents the introduction of paradoxical concepts and ensures that the definition is rigorous and grounded in the formal mathematical framework of limits.
What is the relationship between the derivative of a function and its rate of change?
-The derivative of a function at a specific point is the precise measure of the rate of change of the function at that point. It represents the instantaneous rate of change, which can be used to analyze the behavior of the function, such as its increasing or decreasing nature, and the points of maximum or minimum values.
How does the concept of limits help in building a stronger intuition for calculus?
-The concept of limits helps in building a stronger intuition for calculus by providing a concrete way to understand the behavior of functions as they approach certain values or points. This understanding is crucial for grasping the rules of calculus and applying them effectively to solve problems.
Outlines
📚 Introduction to Limits and Derivatives
The paragraph introduces the concept of limits in calculus, explaining that limits are a way to describe how one value approaches another. It emphasizes the importance of understanding limits to grasp the formal definition of derivatives. The speaker reassures viewers that the intuitive idea of 'dx' and 'df' as concrete, non-zero nudges is supported by the rigorous formal definition of derivatives. The paragraph also mentions the epsilon-delta definition of limits and introduces L'Hopital's rule as a method for computing limits in certain scenarios.
📈 Understanding the Epsilon-Delta Definition of Limits
This paragraph delves into the epsilon-delta definition of limits, providing a rigorous way to define what it means for one value to approach another. It uses the example of a function with an undefined value at a certain point, but where the function's graph approaches a specific value as the input gets closer to that point. The paragraph contrasts this with a function that does not approach a unique value, thereby lacking a defined limit. The epsilon-delta definition is introduced as a method to determine whether a limit exists by examining how the output values behave as the input values are shrunk around the limiting point.
🔢 Application of Derivatives in Evaluating Limits
The paragraph discusses the application of derivatives in evaluating limits, particularly in cases where the direct substitution of a value into a function results in an undefined expression (0/0). It uses the example of a function that is undefined at x=1 but approaches a specific limit value. The speaker explains how to approximate the limit by considering the behavior of the function just slightly away from the undefined point and how derivatives can be used to find this limit. This method is a precursor to L'Hopital's rule, which is introduced as a systematic way to evaluate such limits.
🎓 L'Hopital's Rule and its Historical Context
This paragraph introduces L'Hopital's rule as a powerful tool for computing limits when direct substitution results in an indeterminate form. It explains the rule by considering the ratio of two functions that are both zero at a certain point and shows how the limit of this ratio can be found by taking the ratio of their derivatives. The paragraph also provides historical context, noting that L'Hopital's rule was originally discovered by Johann Bernoulli but named after Guillaume de l'Hôpital due to his interest in the discovery. The speaker concludes by connecting the concept of limits to the upcoming topic of integrals and the fundamental theorem of calculus.
Mindmap
Keywords
💡Derivative
💡Limit
💡Epsilon-Delta Definition
💡L'Hopital's Rule
💡Function
💡Nudge
💡Rise over Run
💡Continuous
💡Indeterminate Form
💡Real Analysis
Highlights
Introduction to the concept of limits as an extension of the intuitive understanding of the word 'approach'.
Explanation of the formal definition of a derivative and how it relates to the concept of limits.
Clarification on the use of 'dx' and 'df' as concrete non-zero nudges, supported by the formal definition of a derivative.
Introduction to the epsilon-delta definition of limits to precisely define the idea of 'approach'.
Discussion of L'Hopital's rule as a clever method for computing limits.
Explanation of how derivatives and the idea of limits are interconnected, with a focus on the formal definition of a derivative.
Demonstration of how to calculate limits using L'Hopital's rule through practical examples.
Insight into how mathematicians think about functions and limits in calculus, using real analysis principles.
The significance of avoiding the paradoxical concept of infinitely small changes by using limits.
Illustration of how the graph of a function can inform about its limit, with examples of undefined points.
Explication of the epsilon-delta criterion for the existence of limits and its implications for calculus.
Discussion on the non-existence of limits in certain functions and the mathematical reasoning behind it.
Application of derivative concepts to understand and compute limits of functions that are not immediately obvious.
Reiteration of L'Hopital's Rule and its historical context, highlighting the collaboration between Johann Bernoulli and L'Hopital.
Future topics including integrals and the fundamental theorem of calculus, promising further exploration of limits.
Mention of support for the channel through Patreon and introduction of a 3blue1brown store for the community.
Transcripts
Browse More Related Video

Limits and Continuous Functions
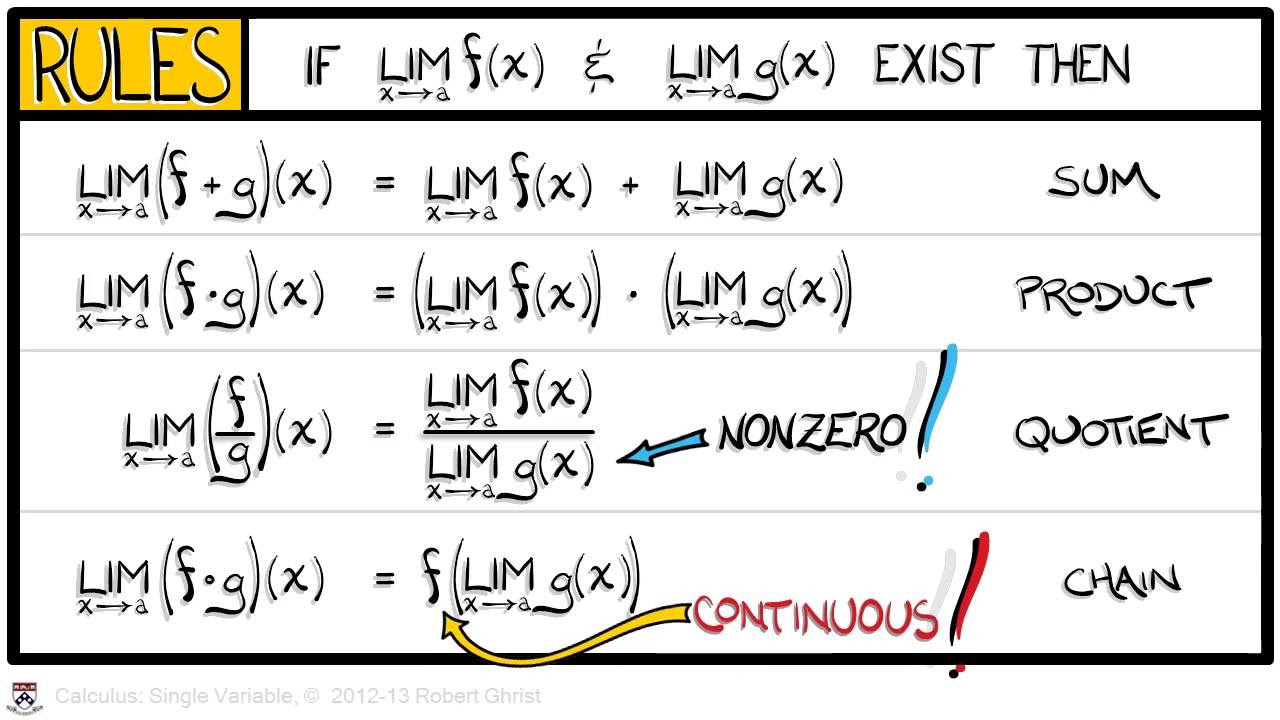
Calculus Chapter 1 Lecture 7 Limits

Lecture 13: Achilles, Tortoises, Limits and Continuity

2021 Live Review 3 | AP Calculus AB | How to Find Limits & Continuity

Epsilon-Delta Definition of Functional Limits | Real Analysis

Limits in Calculus: Definition & Meaning. What is a Limit?
5.0 / 5 (0 votes)
Thanks for rating: