The second most beautiful equation and its surprising applications
TLDRThis video explores Euler's identity and characteristic, delving into their mathematical beauty and applications. It explains how Euler's characteristic, a topological invariant, applies to various shapes, including polyhedra and spheres, and introduces the Poincare-Hopf theorem linking vector fields to Euler's characteristic. The video also touches on curvature, Gaussian curvature, and their relation to the Gauss-Bonnet theorem, illustrating the connection between local geometry and global topology. Curiosity Stream, the sponsor, offers a wealth of documentaries for the curious-minded.
Takeaways
- 🧡 Euler's identity is celebrated as one of the most beautiful equations in mathematics, elegantly relating the fundamental constants e, i, π, 1, and 0.
- 🏆 The second most beautiful equation is subjective, but Euler's characteristic, specifically when it equals 2, is a popular choice among mathematicians.
- 📐 Euler's characteristic (V - E + F = 2) applies to convex polyhedra, indicating the relationship between vertices, edges, and faces, always summing to 2.
- 🌐 The concept extends to more complex shapes like a sphere, where Euler's characteristic also equals 2, even when considering great circles as edges and vertices.
- 🔗 Euler's characteristic is preserved under homeomorphisms, meaning it remains the same for shapes that can be continuously deformed into one another without tearing or gluing.
- 🍩 Shapes like a torus have an Euler's characteristic of 0, which is calculated by considering vertices, edges, and faces on the surface, including those formed by wrapping paths.
- 🔍 The Euler's characteristic can also be thought of as 1 minus twice the number of holes in a shape, highlighting its relationship with the shape's topology.
- 🌀 The Poincare-Hopf theorem links the Euler characteristic to the behavior of continuous vector fields on a surface, particularly how indices of zero vectors sum to the Euler characteristic.
- 📚 The hairy ball theorem, which states that there must be at least one point of zero wind on a sphere, is a corollary of the Poincare-Hopf theorem and demonstrates the inevitability of certain topological features.
- 📏 Curvature, particularly Gaussian curvature, is a key concept in understanding the geometry of surfaces, distinguishing between flat, positively curved, and negatively curved spaces.
- 🌀 The Gauss-Bonnet theorem ties together the total curvature of a surface with its Euler characteristic, showing a deep connection between local geometric properties and global topological ones.
Q & A
What is Euler's identity and why is it considered beautiful in mathematics?
-Euler's identity is an equation that surprisingly relates five fundamental constants: e, i, π, 1, and 0. It is considered beautiful because of its elegance in connecting these constants in a simple and profound way.
What is Euler's characteristic and how does it relate to convex polyhedra?
-Euler's characteristic is a topological invariant that for any convex polyhedron equals to the number of vertices minus the number of edges plus the number of faces, always resulting in 2. It is a measure of the 'shape' of a polyhedron that remains constant under continuous deformations.
How does Euler's characteristic apply to a sphere?
-For a sphere, the Euler's characteristic is also 2. This can be visualized by considering the intersections of great circles as vertices and the segments between these vertices as edges and faces, leading to the same formula of vertices - edges + faces = 2.
What is the significance of Euler's characteristic in the context of homeomorphisms?
-Euler's characteristic is preserved under homeomorphisms, meaning that if you can continuously deform one shape into another without tearing or gluing, the Euler's characteristic will remain the same, indicating a topological equivalence.
How does Euler's characteristic differ between a sphere and a torus?
-A sphere has an Euler's characteristic of 2, while a torus has an Euler's characteristic of 0. This difference indicates that a sphere and a torus are topologically distinct and cannot be deformed into one another without creating or eliminating holes.
What is the Poincare-Hopf theorem and how does it relate to Euler's characteristic?
-The Poincare-Hopf theorem states that for a continuous vector field with isolated zeroes on a surface, the sum of the indices of these zeroes equals the Euler characteristic of that surface. This theorem connects local properties of vector fields to the global topological property of Euler's characteristic.
How is the concept of curvature related to Euler's characteristic in the Gauss-Bonnet theorem?
-The Gauss-Bonnet theorem links the total curvature of a surface, which is a geometric property, to its Euler characteristic, which is a topological property. It states that the total curvature of a surface equals 2π times its Euler characteristic.
What is the hairy ball theorem and how does it relate to the Poincare-Hopf theorem?
-The hairy ball theorem is a corollary of the Poincare-Hopf theorem, stating that there is always at least one point on a sphere where the tangent vector field has a zero (like a cowlick in hair). It demonstrates the impossibility of combing hair on a sphere without creating such a zero vector.
How does Euler's characteristic apply to flat surfaces and grid-based polygons?
-For flat surfaces, Euler's characteristic can be used to prove Pick's theorem, which calculates the area of a polygon on a grid based on the number of points on its boundary and interior. It also plays a role in the five color theorem, which is related to map coloring problems.
What is the significance of the angle excess or deficit in geodesic triangles on a sphere?
-The angle excess or deficit in geodesic triangles on a sphere corresponds to the total curvature enclosed by the triangle. For a sphere with positive Gaussian curvature, the angles in a geodesic triangle add up to more than 180 degrees, reflecting the positive curvature.
How does the total curvature of a surface relate to its Euler characteristic and Gaussian curvature?
-According to the Gauss-Bonnet theorem, the total curvature of a surface, which is the integral of its Gaussian curvature, is equal to 2π times its Euler characteristic. This relationship shows that the total curvature is determined by both the local curvature properties and the global topological properties of the surface.
Outlines
📚 Euler's Identity and the Beauty of Mathematics
The script introduces Euler's identity as one of the most beautiful equations in mathematics, elegantly linking five fundamental constants: e, i, π, 1, and 0. It then discusses the concept of the second most beautiful equation, which is more subjective but often attributed to Euler's characteristic. This characteristic is exemplified in the equation V - E + F = 2, applicable to convex polyhedra, where V stands for vertices, E for edges, and F for faces. The script provides a visual tour through the five platonic solids, demonstrating how each adheres to Euler's characteristic, even when considering a sphere, which is treated as a special case with two vertices, four edges, and four faces, all summing to an Euler characteristic of 2. The concept is further explored in the context of homeomorphisms, where shapes can be continuously deformed without losing their Euler characteristic, unless holes are introduced or removed.
🌐 Exploring Euler's Characteristic and Vector Fields
This paragraph delves into the applications of Euler's characteristic, particularly in relation to vector fields on surfaces. It uses the example of a hypothetical torus with a constant wind represented by a vector field, illustrating how zero vectors, or points with no wind, relate to the Euler characteristic. The concept of indices for zero vectors in continuous vector fields is introduced, with different types of zero vectors—centers, saddles, sources, and sinks—having indices that can be determined by the rotation of a dial around them. The Poincare-Hopf theorem is then explained, connecting the sum of these indices to the Euler characteristic of the surface. The 'hairy ball theorem' is highlighted as a humorous application of this concept, demonstrating that a sphere cannot be combed without creating at least one cowlick, or zero vector.
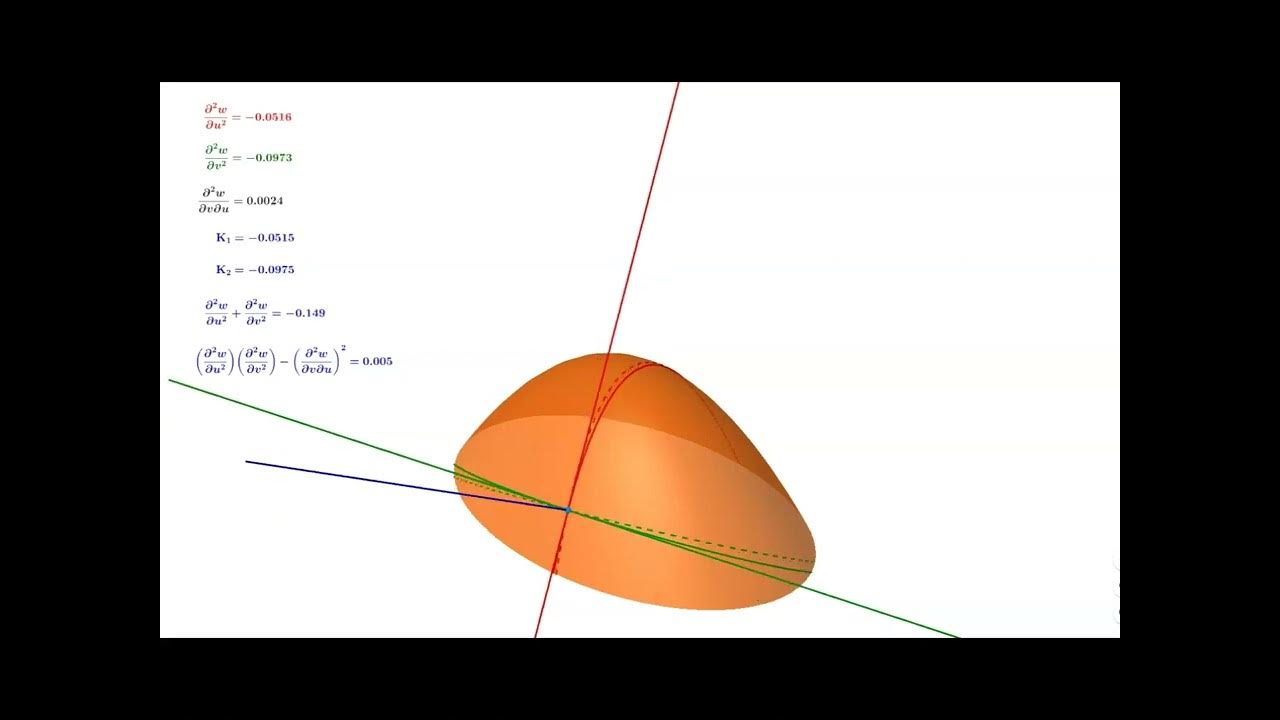
📐 Curvature and the Intricacies of Plane and Surface Geometry
The script shifts focus to the concept of curvature, starting with the physical intuition of curvature for plane curves as the rate of rotation of the tangent vector along the curve. It distinguishes between positive and negative curvature and uses the circle as an example to explain how curvature is related to the radius. The total curvature of a circle and its relation to the circle's geometry is discussed, emphasizing that the total curvature remains constant at 2π regardless of the circle's size. The explanation extends to polygons and their vertices, showing that the total curvature is also 2π for these shapes, which can be deformed from a circle. Gaussian curvature is introduced for surfaces, contrasting it with the curvature of plane curves and explaining how it is calculated using principal curvatures. The script concludes with examples of surfaces with positive, negative, and zero Gaussian curvature, including a sphere, a shaver, and a peculiar object that, despite appearing curved, has zero Gaussian curvature due to the perpendicular segments canceling each other out.
🌀 Geodesic Triangles, Curvature, and the Gauss-Bonnet Theorem
This section explores the relationship between geodesic triangles on a sphere and their curvature, noting that the angles in these triangles do not sum to the typical 180 degrees found in Euclidean geometry. Instead, they sum to 270 degrees, indicating an 'excess' of 90 degrees that corresponds to the enclosed curvature. The Gauss-Bonnet theorem is introduced, linking the total curvature of a surface to its Euler characteristic, with a focus on how this relationship holds for various shapes, including the platonic solids. The script explains how the angle deficit or excess in geodesic triangles directly relates to the enclosed curvature, and how this is consistent across different surfaces, regardless of their specific geometric properties. The concept is applied to a torus, demonstrating how the positive and negative curvatures cancel out, resulting in a total curvature of zero, aligning with its Euler characteristic.
🌌 Euler's Characteristic in Various Mathematical and Physical Contexts
The final paragraph discusses the wide-ranging applications of Euler's characteristic, from proving Pick's theorem for calculating the area of polygons on a grid to the four and five color theorems in graph theory. It also mentions the relevance of curvature in general relativity and the curvature of the universe. The script concludes by recommending the book 'Euler's Gem' for further exploration of Euler's characteristic, knot theory, and higher dimensions, and promotes Curiosity Stream as a resource for learning about various scientific and technological topics. A special offer for the first month's free membership to Curiosity Stream is provided for viewers interested in its content.
Mindmap
Keywords
💡Euler's Identity
💡Euler's Characteristic
💡Convex Polyhedron
💡Platonic Solids
💡Homeomorphisms
💡Torus
💡Poincare-Hopf Theorem
💡Curvature
💡Gauss-Bonnet Theorem
💡Geodesic
💡Four Color Theorem
Highlights
Euler's identity is considered the most beautiful equation in mathematics, relating e, i, Pi, 1, and 0.
Euler's characteristic is often cited as the second most beautiful equation and relates vertices, edges, and faces of convex polyhedra.
The Euler's characteristic equation V - E + F = 2 holds true for all convex polyhedra, including the sphere.
A sphere's Euler's characteristic is demonstrated through the intersection of great circles, resulting in 2 vertices, 4 edges, and 4 faces.
Euler's characteristic is preserved under homeomorphisms, meaning it remains the same through continuous deformations without holes or tears.
A torus, unlike a sphere, has an Euler's characteristic of zero, which is visualized by drawing circles around it.
The Euler's characteristic can also be defined as 1 minus the number of holes in a shape, as demonstrated with a torus.
Euler's characteristic applies to flat surfaces as well, with vertices, edges, and faces summing to 1 in various configurations.
The Poincare-Hopf theorem links the indices of zero vectors in continuous vector fields to the Euler characteristic of the surface.
The hairy ball theorem, a humorous yet rigorous proof in mathematics, is a special case of the Poincare-Hopf theorem.
Curvature, both in plane curves and Gaussian curvature for surfaces, is discussed with respect to their topological implications.
The Gauss-Bonnet theorem connects the total curvature of a surface with its Euler characteristic, showing a relationship between local and global properties.
The total curvature of a sphere, regardless of size, is consistently 4 pi, demonstrating the constancy of curvature in homeomorphic shapes.
Geodesic triangles on a sphere have an angle excess that matches the enclosed total curvature, a relationship that holds for both positive and negative Gaussian curvature surfaces.
The Euler's characteristic is used to prove Pick's theorem, which calculates the area of polygons on a grid based on boundary and interior points.
The five color theorem, though surpassed by the four color theorem, is another application where Euler's characteristic plays a role.
Curiosity Stream, the sponsor of the video, offers a streaming service with thousands of documentaries and nonfiction titles across various subjects.
The video concludes with a promotion for Curiosity Stream, offering a free first-month membership with the promo code MajorPre.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: