11. Radioactivity and Series Radioactive Decays

MIT OpenCourseWare

20 Sept 201954:11

EducationalLearning

32 Likes 10 Comments

TLDRThe transcript discusses the concept of series decay and its application in nuclear activation analysis. The lecture delves into the derivation of decay equations, explaining the relationship between decay constants, activity, and the amount of substance. It further explores the dynamics of nuclear activation analysis, including the impact of reactor operation on isotope production and decay. The importance of understanding decay chains and the ability to predict isotope behavior as a function of time is emphasized, with a focus on graphical and mathematical problem-solving methods.

Takeaways

📚 The lecture is about series decay, a challenging topic in nuclear physics, and its application in nuclear activation analysis.
🧪 The class conducted an interactive session where students brought in various samples like aluminum foil and rubber stopper for nuclear activation analysis.
📈 The concept of activity in decay, measured in becquerels (BQ) or curies (Ci), was discussed, with emphasis on their significance in quantifying radioactive decay.
🔄 The derivation of differential equations for isotopes N1, N2, and N3 was covered, highlighting the relationship between production and destruction rates in nuclear decay processes.
🎓 The lecture corrected a previous mistake regarding the integrating factor in solving differential equations for nuclear decay, emphasizing the importance of accurate calculations.
📊 The professor introduced a graphing calculator tool to visualize the concentration of isotopes over time, aiding in understanding the behavior of radioactive decay.
🤔 The session explored the use of limiting cases to understand the behavior of isotopes graphically without solving the differential equations algebraically.
🌟 The concept of nuclear activation analysis was explained, detailing how isotopes can be produced and destroyed in a reactor, and how this information can be used to determine impurities in materials.
🚫 The discussion clarified that certain isotopes may not follow the same decay paths as their decay products, which is crucial for accurate nuclear activation analysis.
⏱️ The impact of reactor shutdown on the decay process was discussed, noting that while neutron production stops, natural decay continues.
📝 The lecture concluded with an emphasis on the importance of understanding the physics behind nuclear decay and activation analysis for practical applications.

Q & A

What is the main topic of the lecture?
-The main topic of the lecture is series decay, with a focus on nuclear activation analysis.
What is the definition of activity in the context of radioactive decay?
-Activity is defined as the decay constant times the amount of substance present, and its units are 1 over second (s^-1).
What are the two units mentioned for measuring radioactive decay, and what do they represent?
-The two units mentioned are becquerels (BQ) and curies (Ci). One becquerel represents one decay per second, while one curie represents a much larger number of decays per second, making it more manageable for highly radioactive substances.
How does the lecturer suggest students prepare for a homework assignment involving impurities in samples?
-The lecturer suggests that students bring in samples (not hair or salty substances) in a plastic baggie with their name on it, and they will use the isotopes from a shortlist provided on the learning module site to determine the impurities and their quantities in the samples.
What is the basic form of the differential equations describing the rate of change for each isotope in the series decay example?
-The basic form of the differential equations is change = production - destruction, where change equals the decay constant times the amount of substance, production is the decay of the preceding isotope, and destruction is the decay of the current isotope.
How does the lecturer correct a mistake from a previous lecture regarding the integrating factor in solving differential equations for series decay?
-The lecturer corrects the mistake by showing that the integrating factor is not zero and that it should have been included in the previous derivation. The integrating factor is a function that helps to simplify the differential equation into a form that can be easily integrated.
What is the significance of the conservation equation in the context of the lecture?
-The conservation equation is significant because it states that the total amount of all atoms in the system must remain constant over time, which helps in solving for the concentrations of the isotopes without having to solve for each individual isotope separately.
What is the role of the graphical method in solving differential equations for series decay?
-The graphical method helps in understanding the behavior of the solutions to the differential equations by visually representing the decay and buildup of the isotopes over time. It allows students to predict the values and slopes of the isotopes as a function of time without having to solve the equations algebraically.
What is the concept of 'burning' in the context of nuclear activation analysis?
-In the context of nuclear activation analysis, 'burning' refers to the process where an isotope absorbs neutrons in a reactor and undergoes a reaction, which can change its properties or transform it into a different isotope. This process is important to consider as it can affect the decay signature of the isotope being analyzed.
How does the lecturer plan to enhance the students' understanding of the material?
-The lecturer plans to enhance the students' understanding by providing a numerical example with real numbers and a graphical calculator to help them visualize and interact with the concepts of series decay and nuclear activation analysis. This hands-on approach is intended to solidify their grasp of the material.

Outlines

00:00

📚 Introduction to Series Decay and Nuclear Activation Analysis

The paragraph introduces the topic of series decay and sets the stage for a discussion on nuclear activation analysis. It emphasizes the importance of understanding series decay before diving into the specifics of nuclear activation analysis. The lecturer, Michael Short, humorously reminds students to bring in samples for analysis, highlighting the practical application of the concepts being taught. The summary of the derivation of series decay is also mentioned, along with an introduction to the concept of activity in terms of decays per unit volume per second.

05:01

🧮 Deriving the Differential Equations for Series Decay

This section delves into the mathematical derivation of the differential equations governing the rate of change of isotopes in a series decay scenario. The paragraph explains the process of setting up the equations using the concept of change equaling production minus destruction. It also outlines the integration factor method used to solve these differential equations, emphasizing the importance of considering the total amount of atoms in the system for the solution.

10:03

📈 Graphical Analysis of Isotope Concentration Over Time

The paragraph focuses on the graphical representation of isotope concentration changes over time. It discusses the initial and limiting behaviors of the isotopes' concentrations, using the conservation equation to understand the system's behavior. The lecturer corrects a previous mistake regarding the integrating factor and demonstrates how to arrive at the solution for N2, emphasizing the importance of not assuming values without proper calculation.

15:05

🔬 Nuclear Activation Analysis: Practical Application and Calculations

This section introduces the concept of nuclear activation analysis, a practical application of the series decay model. The lecturer explains how to use the model to determine impurities in a sample by analyzing the decay of isotopes. The importance of considering isotopes on a shortlist is highlighted, and the limitations of the analysis, such as the inability to detect all impurities, are discussed. The paragraph also touches on the process of irradiation and counting for nuclear activation analysis.

20:10

🤔 Understanding Limiting Behaviors in Decay Systems

The paragraph discusses the limiting behaviors of isotopes at the start and end of a decay process. It provides a method to intuitively understand the behavior of the system without solving differential equations. The讲师, Michael Short, guides the audience through determining the behavior of N1, N2, and N3 at t=0 and t=∞, and how to find the point where N2 reaches its maximum value. This approach helps in understanding the general trends in decay systems.

25:11

📉 Decay and Production of Isotopes in a Reactor Environment

This section explores the behavior of isotopes when subjected to a reactor environment, focusing on the production and destruction rates of n1, n2, and n3. The paragraph explains the impact of the reactor's neutron flux on these rates and how the equations for nuclear activation analysis in a reactor are derived. The conditions when the material is removed from the reactor are also discussed, emphasizing the cessation of neutron-induced reactions.

30:12

🔍 Visualizing Decay Processes with Varying Half-Lives

The paragraph investigates how varying half-lives of isotopes affect their decay processes. It discusses the physical implications of having isotopes with significantly different half-lives and how this affects the graphical representation of their decay. The lecturer uses graphical adjustments to illustrate the decay processes for different relative half-lives, providing a visual understanding of the decay dynamics.

35:15

📝 Setting Up and Solving Differential Equations for Decay Chains

This section encourages students to become comfortable with setting up and solving sets of differential equations for decay chains. The lecturer offers to spend more time on the topic if needed and suggests using graphical methods to understand limiting cases. The importance of being able to predict the values and slopes of isotopes as a function of time is emphasized, as this skill is crucial for nuclear activation analysis.

40:17

🤔 Handling Spontaneous Fission and Electron Capture in Decay Calculations

The paragraph addresses questions related to spontaneous fission and electron capture in nuclear decay calculations. It discusses the selection of fission products and the calculation of Q values for electron capture. The lecturer clarifies that for electron capture, the binding energy of the innermost shell electron is typically used and that the process of Auger electron emission can be considered regardless of the initial radiation type.

45:18

🚀 Creativity in Nuclear Reactions to Produce Specific Isotopes

This section challenges students to think creatively about inducing nuclear reactions to artificially produce specific isotopes, such as molybdenum-99. The paragraph encourages considering all possible particles that could be used to create the desired isotope and evaluating the feasibility of these reactions in terms of energy requirements and practicality. The importance of innovation in solving complex nuclear chemistry problems is highlighted.

Mindmap

Keywords

💡Nuclear Activation Analysis

Nuclear activation analysis is a technique used to determine the impurities in a sample by irradiating it in a nuclear reactor and then measuring the radioactive decay of the induced isotopes. In the script, this concept is central as the lecturer discusses how students will be using the technique to analyze various materials, such as aluminum foil and rubber stoppers, to identify impurities within them.

💡Half-life

The half-life of a radioactive substance is the time required for half of the substance to decay. It is a fundamental concept in understanding the behavior of radioactive decay, as discussed in the script where the lecturer explores how different half-lives affect the decay process and the resulting concentrations of isotopes.

💡Isotopes

Isotopes are variants of a particular chemical element which differ in neutron number, and hence in nuclear properties. The script discusses isotopes in the context of a decay series, where one isotope (N1) decays to another (N2), and so on, highlighting the importance of understanding the behavior of isotopes in nuclear reactions.

💡Radioactive Decay

Radioactive decay is the process by which an unstable atomic nucleus loses energy by emitting radiation. The script delves into the mathematical representation and graphical interpretation of this process, particularly focusing on how the decay of one isotope can lead to the creation and subsequent decay of another.

💡Activity

Activity refers to the decay constant times the amount of substance, and it is a measure of the number of decays per unit time. The unit for activity is the becquerel (BQ), which is defined as one decay per second. The concept is integral to the script as it discusses how to calculate and interpret the activity of various isotopes.

💡Decay Constant

The decay constant is a measure of the probability per unit time that a particle will decay. It is denoted by the symbol λ and has units of inverse time (e.g., 1/second). In the script, the decay constant is used in differential equations to describe the rate of change of isotopes within a decay series.

💡Flux

Flux, in the context of the script, refers to the rate of particles, such as neutrons, passing through a given surface area per unit time. It is a crucial parameter in nuclear activation analysis as it determines the rate at which isotopes are activated (induced to become radioactive) by the absorption of neutrons.

💡Cross Section

The cross section, often measured in barns, is a measure of the probability that a nuclear reaction will occur. It is used to quantify the likelihood of a specific interaction, such as a neutron being absorbed by a nucleus. In the script, the cross section is a key factor in determining the rate of production of isotopes during irradiation.

💡Control Rods

Control rods are used in nuclear reactors to control the rate of the nuclear chain reaction. They typically absorb neutrons, thus reducing the reactor's power. The script mentions control rods in the context of shutting down the reactor to prevent neutron-induced reactions when samples are removed for analysis.

💡Spontaneous Fission

Spontaneous fission is a process in which a heavy nucleus like uranium splits into two medium-sized nuclei without any external cause. The script briefly touches on this as a possible reaction for certain isotopes, highlighting the complexity of nuclear reactions and decay processes.

💡Electron Capture

Electron capture is a process in which a proton-rich nucleus captures an electron from an inner electron shell and converts a proton into a neutron. This process results in a decrease in the atomic number of the atom. The script discusses this as a possible nuclear reaction that students might consider when analyzing decay processes.

💡Auger Electrons

Auger electrons are emitted in a process known as the Auger effect, where an electron fills a vacancy in an inner electron shell and another electron is ejected to conserve energy. The script mentions Auger electrons in the context of secondary electron emission following the interaction of gamma rays or other high-energy particles with matter.

Highlights

Series decay is a difficult topic, and the lecture aims to re-explore the derivation and delve into nuclear activation analysis.

The lecture introduces a practical activity where students bring in everyday items like aluminum foil and rubber stoppers to analyze for impurities using nuclear activation analysis.

The concept of activity in decay is explained, which is the decay constant times the amount of substance, measured in becquerels (BQ) or curies (Ci).

Differential equations describing the rate of change for isotopes in a decay series are derived and discussed, emphasizing the relationship between production and destruction rates.

The lecture corrects a previous mistake regarding the integrating factor in solving differential equations for nuclear decay, demonstrating the importance of precision in scientific analysis.

A graphical calculator is introduced as a tool for students to visualize and understand the behavior of isotopes in a decay series.

The lecture explores the limiting behavior of isotopes at the beginning (t=0) and end (t=∞) of their decay process, providing a method for solving problems graphically.

The concept of nuclear activation analysis is introduced, explaining how isotopes can be produced and destroyed in a reactor, and how this can be used to determine impurities in materials.

The units of decay equations and reaction rates are discussed, emphasizing the need for consistency in units for accurate analysis.

The lecture explains the process of shutting down a reactor and the impact on neutron flux, which is crucial for understanding the behavior of isotopes post-irradiation.

The importance of statistical analysis in determining the correct activity of isotopes and the trade-off between counting time and precision is discussed.

The lecture encourages students to think conceptually and use graphical, mathematical, and intuitive methods to predict the values and slopes of isotopes as a function of time.

The impact of varying half-lives on the decay process is explored, showing how the relative half-lives of isotopes affect their decay and buildup over time.

The lecture concludes with a commitment to provide a numerical example of nuclear activation analysis in a future session, reinforcing the practical application of the concepts discussed.

Transcripts

Browse More Related Video

10. Radioactive Decay Continued

12. Numerical Examples of Activity, Half Life, and Series Decay

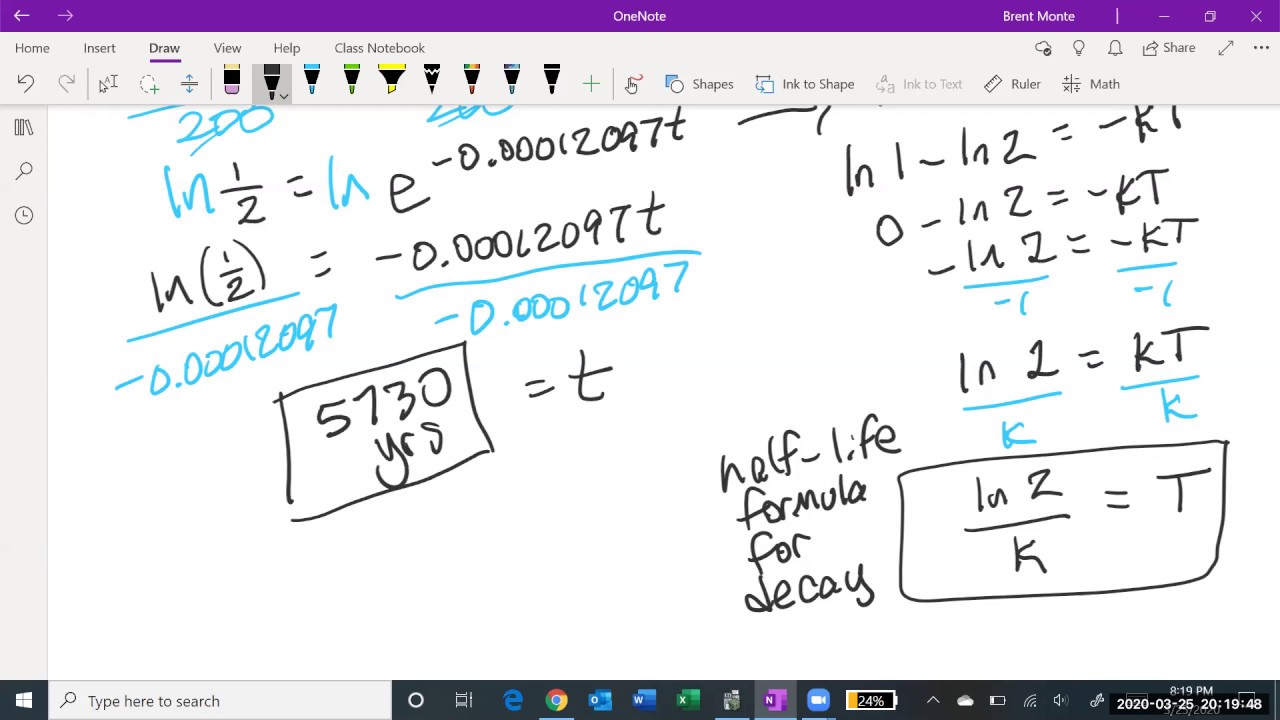
Exponential decay formula proof (can skip, involves calculus) | Chemistry | Khan Academy

31. Nuclear Chemistry and Chemical Kinetics

Math 11 - Section 2.5 (previously section 3.4)

15.4 Kinetics of Nuclear Decay | High School Chemistry

Related Tags

Nuclear Activation Radioactive Decay Isotope Analysis MIT Lecture Educational Resource Physical Science Mathematical Modeling Half-life Neutron Flux Reactor Dynamics Science Education