Physics 15 Torque Fundamentals (13 of 13) Torque and Angular Acceleration

Michel van Biezen
11 Jun 201603:48
EducationalLearning
32 Likes 10 Comments

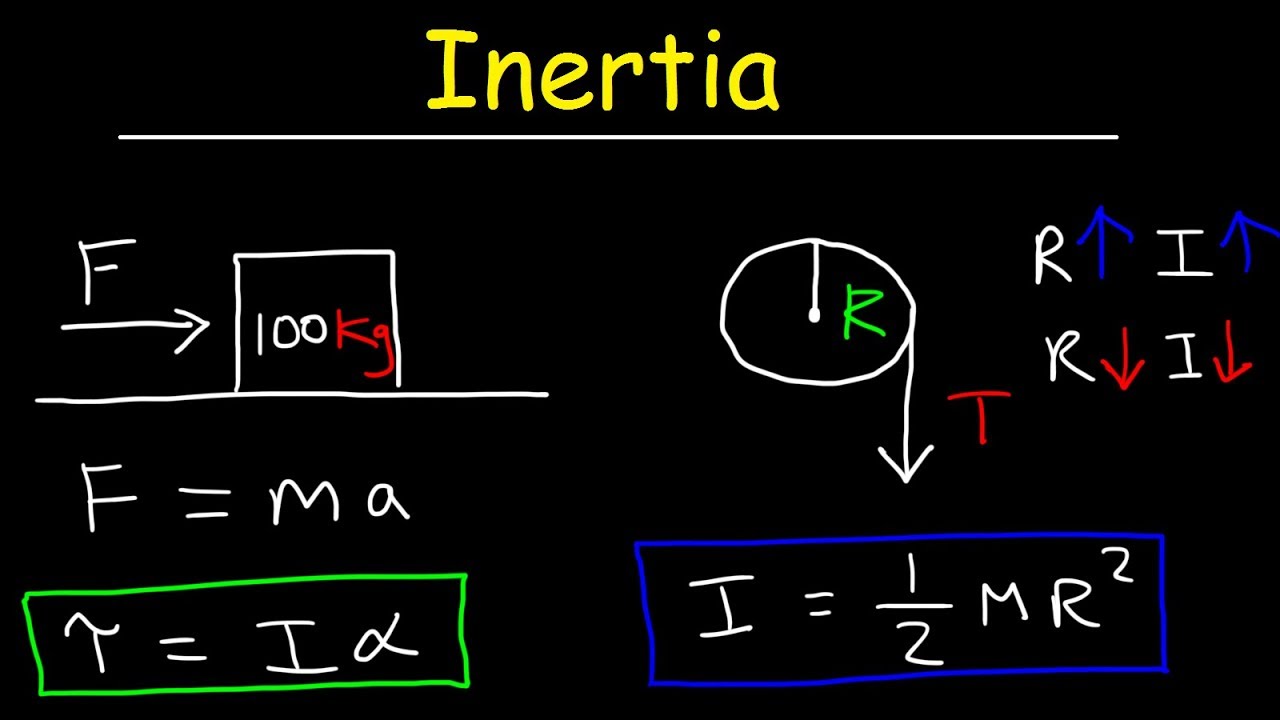
TLDRThe video script explores the concept of angular acceleration caused by a net torque on a rotating disc. It explains that the moment of inertia for a solid disc is given by one-half the product of mass (M) and the square of the radius (R). Using the given radius of 25 cm, mass of 4 kg, and a force of 50 Newtons, the script demonstrates how to calculate the torque and subsequently the angular acceleration. The formula for torque is the force multiplied by the radius, and the angular acceleration (α) is the torque divided by the moment of inertia. After substituting the values, the script concludes that the magnitude of the angular acceleration is 100 radians per second squared. The direction of the force causes a clockwise torque, which is negative, and thus results in a negative angular acceleration. The summary emphasizes the step-by-step process and the importance of considering both magnitude and direction in rotational dynamics.

Takeaways
  • 🌀 A net torque causes an object to have angular acceleration.
  • 📐 The moment of inertia for a solid disc is given by the formula (1/2) * M * R^2, where M is the mass and R is the radius.
  • 🎯 The radius of the disc in the example is 25 centimeters.
  • 🏋️ The mass of the disc is 4 kilograms and the force applied is 50 Newtons.
  • ⚖️ Newton's second law, F = M * A, can be adapted to rotational motion as torque = moment of inertia * angular acceleration.
  • 🔄 The torque is calculated as the force times the perpendicular distance from the pivot point, which is the radius in this case.
  • 🧮 The angular acceleration (α) is the torque divided by the moment of inertia.
  • 🚫 The radius term cancels out when calculating the angular acceleration, simplifying the formula to 2 * (force / mass).
  • 🔢 Substituting the given values, the angular acceleration is calculated as 2 * (50 N / 4 kg) / 0.25 m, which equals 100 rad/s^2.
  • 📐 The units for angular acceleration are radians per second squared (rad/s^2).
  • ➡️ The direction of the force determines the direction of the torque; in this case, it's clockwise, resulting in a negative torque.
  • ❗️ The final answer for the angular acceleration takes into account the negative sign, indicating a clockwise direction of rotation at 100 rad/s^2.
Q & A

  • What is the relationship between net torque and angular acceleration?

    -Net torque causes an object to experience angular acceleration, which is the rate of change of its angular velocity.

  • What is the moment of inertia for a solid disc?

    -The moment of inertia for a solid disc is one-half the product of its mass (M) and the square of its radius (R squared), expressed as I = 1/2 M R^2.

  • What are the given values for the radius and mass of the disc in the script?

    -The radius of the disc is given as 25 centimeters, and the mass of the disc is 4 kilograms.

  • What is the force applied to the disc in the script?

    -The force applied to the disc is 50 Newtons.

  • How is torque related to force in the context of rotational motion?

    -In rotational motion, torque is the equivalent of force in linear motion. It is the product of the force and the perpendicular distance from the pivot point to the line of action of the force.

  • What is the formula to calculate angular acceleration in terms of torque and moment of inertia?

    -The formula to calculate angular acceleration (α) is α = τ / I, where τ is the torque and I is the moment of inertia.

  • What is the direction of the torque and angular acceleration when the force is applied?

    -The direction of the torque and angular acceleration is clockwise, which is considered negative in the context of standard mathematical conventions.

  • How do you convert the units from Newton-meters per kilogram to radians per second squared?

    -Since Newtons are equivalent to kilograms meters per second squared, and the kilograms and meters in the denominator cancel out, you are left with radians per second squared.

  • What is the calculated magnitude of the angular acceleration for the disc?

    -The magnitude of the angular acceleration is 100 radians per second squared.

  • Why is the angular acceleration considered negative in this script?

    -The angular acceleration is considered negative because the force causes a clockwise torque, which in standard mathematical conventions is taken as negative.

  • How does the direction of the torque affect the direction of the angular acceleration?

    -The direction of the torque directly affects the direction of the angular acceleration. A clockwise torque results in a negative angular acceleration, and a counterclockwise torque results in a positive angular acceleration.

  • What is the significance of considering the sign (positive or negative) of the torque and angular acceleration?

    -The sign is significant as it indicates the direction of the rotation. In physics, it's crucial to not only know the magnitude but also the direction of physical quantities such as torque and angular acceleration.

Outlines
00:00
🔧 Angular Acceleration Due to Torque

This paragraph explains the concept of angular acceleration caused by a net torque. It discusses a scenario where a net force acts on a disc that can rotate about a central pivot point, resulting in torque and subsequently angular acceleration. The moment of inertia for a solid disc is given by (1/2) * M * R^2, where M is the mass and R is the radius. Given a radius of 25 cm, a mass of 4 kg, and a force of 50 Newtons, the paragraph walks through the calculation of angular acceleration using the formula torque = moment of inertia * angular acceleration. It emphasizes the cancellation of the radius in the formula, leading to the final expression for angular acceleration as 2 * (force / mass / radius). After substituting the given values and converting units, the angular acceleration is found to be 100 radians per second squared. The direction of the force implies a clockwise rotation, resulting in a negative torque and thus a negative angular acceleration. The paragraph concludes by noting the importance of considering the direction when calculating torque and acceleration.

Mindmap
Keywords
💡Net Torque
Net torque is the total torque acting on an object that can cause it to rotate. In the video, it is mentioned that a net torque causes an angular acceleration, which is essential for understanding the dynamics of the rotating disc. The script uses the concept of net torque to explain how the force applied to the disc results in its rotation around the pivot point.
💡Angular Acceleration
Angular acceleration is the rate of change of angular velocity. It is a key concept in the video as it is the quantity that the video aims to calculate. The script defines it in the context of rotational motion, relating it to the torque applied to a solid disc and its moment of inertia. The example given involves calculating the angular acceleration of a disc subjected to a known force.
💡Moment of Inertia
Moment of inertia is a measure of an object's resistance to rotational motion about a particular axis. For a solid disc, the moment of inertia is calculated as one-half the product of the disc's mass and the square of its radius. In the video, the moment of inertia is used in the formula to find the angular acceleration, showing its importance in rotational dynamics.
💡Pivot Point
The pivot point is the central point around which an object can rotate. In the context of the video, the disc rotates about the pivot point, and the force applied to the disc causes a torque that results in angular acceleration. The pivot point is crucial for understanding the system's rotational dynamics.
💡Solid Disc
A solid disc is a geometric shape that is uniform in density and has a central hole through which it can rotate. The video uses the properties of a solid disc to illustrate the principles of rotational motion. The moment of inertia for a solid disc is given by the formula (1/2)MR^2, which is used in the script to calculate the angular acceleration.
💡Radius
Radius is the distance from the center of a circle to its perimeter. In the video, the radius of the disc is given as 25 centimeters, which is a critical piece of information used to calculate the moment of inertia and subsequently the angular acceleration. The radius is also used to determine the torque experienced by the disc.
💡Mass
Mass is a measure of the amount of matter in an object. The mass of the disc in the video is stated to be 4 kilograms. It is a fundamental property used in the calculation of both the moment of inertia and the resulting angular acceleration when a force is applied.
💡Force
Force is a physical quantity that causes a change in the motion of an object. In the video, a force of 50 Newtons is applied to the disc, which is the cause of the torque and subsequently the angular acceleration. The force is a critical input in the formula used to calculate the torque and the angular acceleration.
💡Newton's Second Law
Newton's second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F=ma). In the rotational context of the video, this law is adapted to relate torque, moment of inertia, and angular acceleration, showing the parallel between linear and rotational motion.
💡Torque
Torque is the rotational equivalent of force and is what causes an object to rotate. In the video, torque is calculated as the product of the force applied and the radius of the disc. It is a key quantity in the formula for calculating angular acceleration and is directly related to the net force acting on the disc.
💡Direction of Rotation
The direction of rotation is important in determining the sign of the torque and angular acceleration. In the video, it is mentioned that the force will cause the disc to spin in a clockwise direction, which results in a negative torque and, consequently, a negative angular acceleration. Understanding the direction of rotation is crucial for correctly interpreting the sign of the calculated quantities.
💡Radian
A radian is a unit of angular measure, used to quantify angles in the context of rotational motion. The video concludes with the angular acceleration being expressed in radians per second squared, which indicates the rate of change of the disc's angular velocity. The radian is a non-SI unit but is essential for describing angular quantities in physics.
Highlights

A net torque causes an angular acceleration

The disc can rotate about the central pivot point

Moment of inertia for a solid disc is 1/2 * M * R^2

Radius of the disc is 25 centimeters

Mass of the disc is 4 kilograms

Force acting on the disc is 50 Newtons

Newton's second law: F = MA

Torque = Moment of Inertia * Angular Acceleration

Torque takes the place of force in rotational motion

Moment of Inertia takes the place of mass

Angular acceleration takes the place of linear acceleration

Angular acceleration (α) = Torque / Moment of Inertia

Torque = Force * Radius

Radius cancels out in the formula

α = 2 * Force / Mass / Radius

Plug in values to get α = 100 rad/s^2

Units are radians per second squared

Force causes clockwise spin and negative torque

Negative torque results in negative angular acceleration

Account for the negative sign for clockwise rotation

Magnitude of angular acceleration is 100 rad/s^2

Transcripts

Browse More Related Video

Rotational version of Newton's second law | Physics | Khan Academy

Falling Box with Pulley | Physics with Professor Matt Anderson | M12-23

Demonstrating Rotational Inertia (or Moment of Inertia)

College Physics 1: Lecture 25 - Moment of Inertia and Rotational Dynamics

AP Physics 1 - Rotational Dynamics

Inertia - Basic Introduction, Torque, Angular Acceleration, Newton's Second Law, Rotational Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Torque CalculationAngular AccelerationNewton's LawsPhysics TutorialRotational MotionMoment of InertiaDisc MechanicsForce ApplicationClockwise TorqueNegative AccelerationPhysics Dynamics