Confidence Level and Margin of Error
TLDRIn this statistics video, the presenter, Rhett, explores the relationship between margin of error and confidence level through a jelly bean guessing game. The game's variations highlight how increasing the acceptable error range boosts confidence among players. The video explains the trade-off between precision and confidence in confidence intervals, emphasizing that a larger margin of error leads to higher confidence levels. It also touches on how critical values from the standard normal distribution determine these intervals, with larger values corresponding to wider intervals and higher confidence.
Takeaways
- 🎲 The video discusses the relationship between margin of error and confidence level in statistics.
- 💰 A guessing game is used as an analogy to explain the concept, with different versions of the game representing varying margins of error.
- 🔢 In the first version of the game, guessing the exact number of jelly beans is required to win, which is akin to a very low margin of error and low confidence.
- 📈 As the acceptable error range increases in subsequent versions of the game, more people are willing to play, reflecting higher confidence levels.
- 🧩 The video illustrates that confidence grows with an increase in the margin of error, and vice versa.
- ⚖️ There is a trade-off between precision (low margin of error) and confidence; being more precise reduces confidence.
- 📊 The margin of error (e) is mathematically represented as the product of the standard error and a multiple, which is determined by the confidence level (C).
- 📉 As the margin of error increases, the confidence level also increases, indicating a direct relationship between the two.
- 📚 The standard error is influenced by the confidence level, which in turn affects the margin of error in confidence intervals.
- 📉 For a statistic that follows a normal distribution, larger critical values (Z scores) correspond to wider intervals and higher confidence levels.
- 🔢 Critical values of plus or minus 1, 2, and 3 correspond to confidence levels of approximately 68%, 95%, and 99.7% respectively.
- 🤔 The video concludes by emphasizing the need to choose between precision and confidence when determining the margin of error in statistical analysis.
Q & A
What is the main topic of the video?
-The main topic of the video is the relationship between margin of error and confidence level in statistics.
Why does the video start with a jelly bean guessing game?
-The jelly bean guessing game is used as an analogy to illustrate the concept of margin of error and how it affects confidence levels in statistical estimation.
What is the cost to play the jelly bean guessing game in all versions?
-In all versions of the game, it costs $5 to play.
In the first version of the game, what are the conditions for winning?
-In the first version, you win $20 if you guess the exact number of jelly beans in the jar.
How does the margin of error change in the second version of the game?
-In the second version, you win if you guess within five of the actual number of jelly beans, effectively increasing the margin of error to plus or minus five.
What is the relationship between margin of error and confidence level as explained in the video?
-As the margin of error increases, the confidence level also increases. Conversely, when the margin of error decreases, the confidence level decreases.
What is the symbol used for margin of error in the video?
-The symbol used for margin of error in the video is 'e'.
What is the symbol used for confidence level in the video?
-The symbol used for confidence level in the video is 'C'.
How does the video explain the trade-off between precision and confidence?
-The video explains that when you require greater precision, your confidence level is lower, and when greater error is allowed, you can be more confident.
What is the role of the standard error in determining the margin of error?
-The standard error, determined by the confidence level, is a key component in calculating the margin of error, which is the product of the standard error and a critical value.
How do critical values or Z scores relate to the confidence level?
-Larger critical values or Z scores correspond to wider intervals of the distribution and higher confidence levels. For example, a critical value of plus or minus 1 corresponds to 68% confidence, plus or minus 2 to 95%, and plus or minus 3 to 99.7% confidence.
Outlines
📊 Understanding Margin of Error and Confidence Level
This paragraph introduces the concept of margin of error and confidence level in statistics through a jelly bean guessing game. It illustrates how the willingness to play the game changes with different versions that have varying degrees of error tolerance. The game versions range from requiring an exact guess to allowing guesses within a range of 100 jelly beans. The paragraph explains that as the margin of error increases, so does the confidence level, and vice versa. It emphasizes the trade-off between precision and confidence in statistical analysis, where a higher precision demands a lower confidence level and a higher margin of error allows for greater confidence.
🔍 The Impact of Confidence Level on Margin of Error
The second paragraph delves into the mathematical relationship between confidence level and margin of error. It explains that the margin of error is calculated as the product of the standard error and a critical value, which is determined by the desired confidence level. The paragraph uses the example of estimating a population mean (mu) with a sample mean (x-bar) plus or minus the margin of error (e). It further clarifies that a wider confidence interval, indicated by larger critical values or Z-scores, corresponds to higher confidence levels but less precision. The paragraph concludes by reiterating the choice between precision and confidence, and encourages viewers to stay rational in their approach to statistical analysis.
Mindmap
Keywords
💡Margin of Error
💡Confidence Level
💡Guessing Game
💡Precision
💡Standard Error
💡Critical Value
💡Confidence Intervals
💡Z Scores
💡Trade-off
💡Normal Distribution
Highlights
Introduction to the concept of the relationship between margin of error and confidence level in statistics.
A guessing game is used to illustrate the concept, where the cost and reward structure changes with different versions.
In the first version of the game, guessing the exact number of jelly beans wins $20, with a $5 cost to play.
The second version allows winning if the guess is within five of the actual number, changing the risk and reward dynamics.
The third version expands the acceptable error to 25, further altering the game's appeal and confidence levels.
In the fourth version, the margin of error is increased to 50, significantly impacting player willingness to participate.
The fifth version pushes the margin of error to 100, drastically changing the confidence level of potential players.
The inverse version five maintains the $5 cost but increases the margin of error to 100, affecting player confidence.
As margin of error increases, so does the confidence level, indicating a trade-off between precision and confidence.
Confidence intervals are explained as a fundamental concept where precision and margin of error are inversely related.
The margin of error (e) and confidence level (C) are symbolized, with e's increase leading to C's increase.
The standard error and a multiple determine the margin of error, which is affected by the confidence level.
Critical values from the standard normal distribution are used to calculate the margin of error for different confidence levels.
A critical value of plus or minus 1 corresponds to a 68% confidence level.
A critical value of plus or minus 2 corresponds to a 95% confidence level.
A critical value of plus or minus 3 corresponds to a confidence level of 99.7%.
The choice between precision and confidence is emphasized as a key decision in statistical analysis.
The video concludes with a reminder of the importance of being rational and staying real in statistical interpretation.
Transcripts
Browse More Related Video

How To Find The Z Score, Confidence Interval, and Margin of Error for a Population Mean

Confidence Interval for a population proportion | Solved Problems

AP Statistics Chapter 8 In-Depth Review Video

Statistics 101: Confidence Intervals, Estimating Sample Size Needed

Confidence Interval for a population mean - t distribution
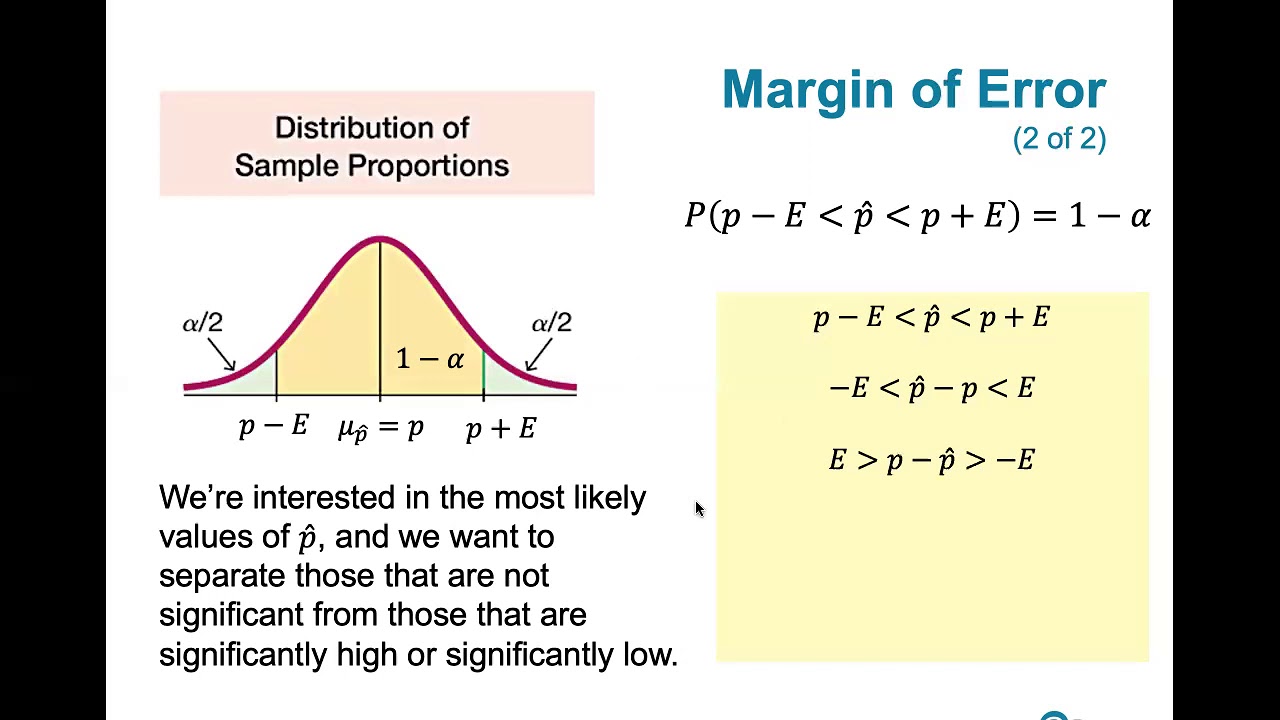
7.1.4 Estimating a Population Proportion - Margin of Error and Computing Confidence Intervals
5.0 / 5 (0 votes)
Thanks for rating: