Gibbs Phase Rule
TLDRThis tutorial video delves into the Gibbs phase rule, a fundamental concept in thermodynamics that determines the number of intensive variables required to define a system's state. The video explains the difference between extensive and intensive variables, and how the rule, expressed as f = c - p + 2, applies to phase changes. Through practical examples, such as heating ice to steam, the tutorial illustrates how the phase rule can be used to understand the relationship between variables like temperature and pressure in various states of matter.
Takeaways
- 🔍 The Gibbs phase rule (f = c - p + 2) is used to determine the number of intensive variables needed to define the state of a system.
- 📚 Extensive variables (like volume, mass, number of moles) depend on the size of the system, while intensive variables (like temperature, pressure, density) do not.
- 🌡 The phase rule applies only to intensive variables, which are crucial for understanding phase transitions and system states.
- 💧 In the example of melting ice, two intensive variables (temperature and pressure) are initially needed to define the state of the ice before melting.
- 🧊 When ice and water coexist, only one intensive variable is needed to define the state, as pressure is constant and temperature is fixed at the melting point.
- 🔥 As the system transitions from ice to water to steam, the number of intensive variables that need to be defined changes according to the phase rule.
- 🌡️ The boiling point of water at one atmosphere of pressure is a specific temperature (100°C), and this is where the phase rule shows one intensive variable is needed.
- 🌬️ In the presence of steam alone, two intensive variables are needed to define the state, as both temperature and pressure can vary independently.
- 🌀 The phase rule equation simplifies to f = 0 at the triple point, where ice, water, and steam coexist at a unique combination of pressure and temperature.
- 📉 The phase diagram is a graphical representation that helps visualize the relationships between phases and the variables that define them.
- 🔑 Understanding the Gibbs phase rule is key to analyzing phase diagrams and predicting the behavior of substances under varying conditions.
Q & A
What is the Gibbs phase rule and what does it determine?
-The Gibbs phase rule is a fundamental principle in thermodynamics that tells us the number of intensive variables that must be defined to determine the state of a system. It helps in understanding the relationship between the components, phases, and the variables required to specify the system's state.
What are the differences between extensive and intensive variables?
-Extensive variables depend on the quantity of the system, such as volume, mass, and the number of moles. Intensive variables, on the other hand, are independent of the system's quantity and include properties like temperature, pressure, and density.
What does the term 'state' mean in the context of the Gibbs phase rule?
-In the context of the Gibbs phase rule, 'state' refers to the complete knowledge of all the variables of a system, including both extensive and intensive variables, which are necessary to fully describe the system.
What is the equation for the Gibbs phase rule and what do the variables represent?
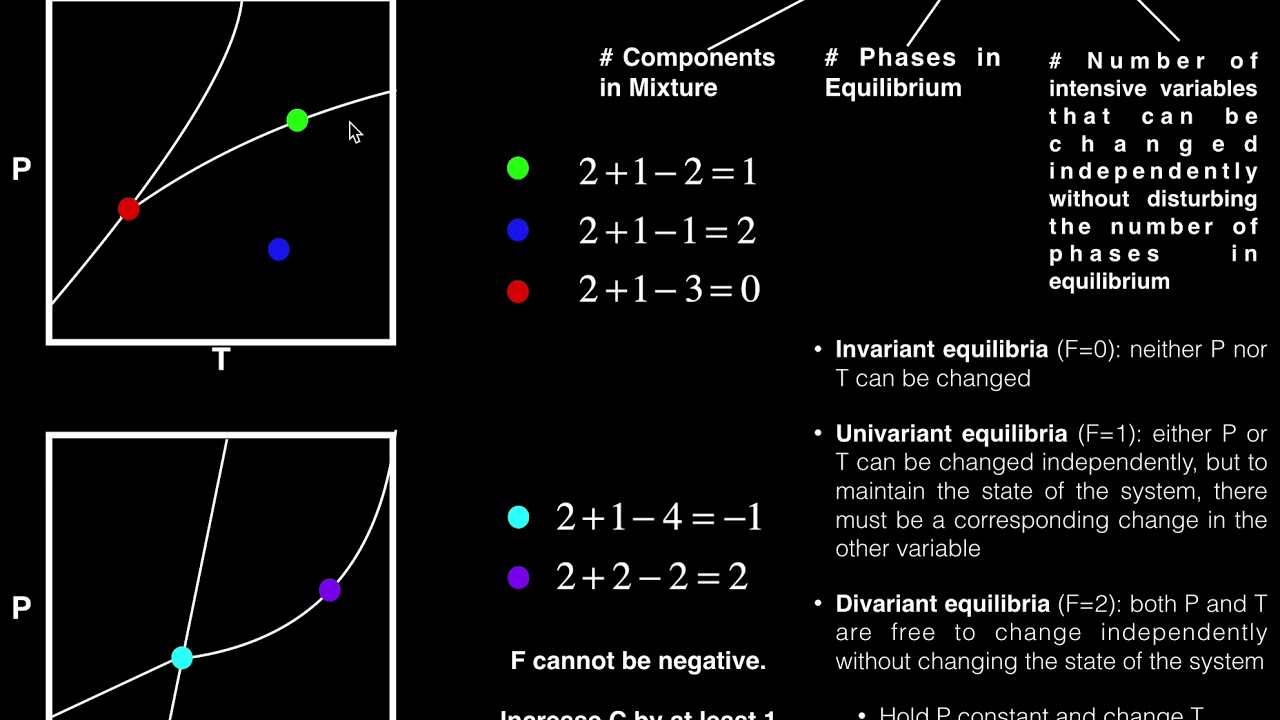
-The equation for the Gibbs phase rule is f = c - p + 2, where 'f' represents the number of intensive variables needed to define the system's state, 'c' is the number of components in the system, 'p' is the number of phases, and '2' is a constant.
How does the Gibbs phase rule apply to phase changes?
-The Gibbs phase rule applies to phase changes by determining the number of variables that need to be controlled or measured to understand the state of a system during a phase transition, such as melting, boiling, or sublimation.
What is an example of a scenario where the Gibbs phase rule would indicate that two variables need to be defined?
-An example is when you have a system with one component (like water) in the solid phase (ice). According to the Gibbs phase rule, you would need to define two variables, such as temperature and pressure, to specify the state of the system.
How does the number of variables required change when a system transitions from one phase to two coexisting phases?
-When a system transitions from one phase to two coexisting phases, the Gibbs phase rule indicates that only one variable needs to be defined, as the system's state is now constrained by the phase equilibrium at a specific temperature and pressure.
What is the significance of the triple point in the context of the Gibbs phase rule?
-At the triple point, where solid, liquid, and gas phases coexist, the Gibbs phase rule indicates that there are zero independent variables to define (f = 0). This is because the system is at a unique point where the pressure and temperature are fixed for the coexistence of all three phases.
Can the variables defined by the Gibbs phase rule be independent of each other?
-Yes, the variables defined by the Gibbs phase rule can be independent of each other, especially when the system is in a single phase. However, when two phases coexist, one variable (usually temperature or pressure) will determine the other at the equilibrium condition.
How does the pressure affect the number of variables needed to define the state of a system according to the Gibbs phase rule?
-The pressure affects the number of variables needed by constraining the system's state. For example, at a constant pressure, the phase rule may indicate that only temperature needs to be defined when two phases coexist, as seen in the case of melting ice or boiling water.
Outlines
🔍 Introduction to the Gibbs Phase Rule
The video script starts with an introduction to the Gibbs phase rule, a fundamental concept in thermodynamics that helps determine the number of intensive variables required to define the state of a system. The script suggests watching a previous tutorial on phase diagrams for better understanding. It explains the difference between extensive and intensive variables, using examples like the volume and mass of water. The Gibbs phase rule is then introduced with the formula f = c - p + 2, where f represents the degrees of freedom, c is the number of components, p is the number of phases, and 2 is a constant. The script emphasizes that the rule applies to intensive variables only.
🌡️ Applying the Gibbs Phase Rule to Phase Changes
The script continues by applying the Gibbs phase rule to a hypothetical experiment involving the heating of ice. It explains how the rule can be used to understand phase transitions, such as melting and boiling. As the ice melts under constant pressure, the script uses the phase rule to illustrate that one intensive variable (temperature) can be determined once the other (pressure) is known. The explanation includes how the phase rule's degrees of freedom change when moving from one phase to a coexistence of two phases, and then to a single phase again, highlighting the independence of intensive variables in different scenarios.
🌟 The Triple Point and Complete Phase Transition
The final part of the script discusses the concept of the triple point, where solid, liquid, and gas phases coexist at a specific pressure and temperature. The Gibbs phase rule is applied to this scenario, resulting in zero degrees of freedom, indicating that both pressure and temperature are uniquely determined. The script wraps up by summarizing the key points of the Gibbs phase rule and its application to phase diagrams, encouraging viewers to ask questions and engage with the content.
Mindmap
Keywords
💡Gibbs phase rule
💡Intensive variables
💡Extensive variables
💡State
💡Phase
💡Components
💡Phase diagram
💡Triple point
💡Degrees of freedom
💡Phase transition
Highlights
Introduction to the Gibbs phase rule tutorial, emphasizing its importance for understanding the state of a system.
Explanation of the difference between extensive and intensive variables, with examples like volume, mass, and temperature.
Clarification that the Gibbs phase rule applies only to intensive variables for determining the system's state.
Definition of 'state' as knowing all the variables of a system, including both extensive and intensive properties.
Presentation of the Gibbs phase rule equation, f = c - p + 2, and its significance in phase diagram analysis.
Description of components (c) as the number of substances in a system, impacting the number of variables needed.
Discussion on phases (p), defined as the number of distinct forms of a substance coexisting in equilibrium.
Illustration of how the Gibbs phase rule is applied to a hypothetical experiment involving ice, water, and steam.
Demonstration of the phase rule's application during the melting of ice, showing the transition from one phase to two phases.
Explanation of how the number of intensive variables required decreases when two phases coexist at a constant pressure.
Use of a phase diagram to visually represent the relationship between pressure, temperature, and phase transitions.
Analysis of the boiling process and its relation to the phase rule, highlighting the single temperature at which water boils at one atmosphere.
Discussion on the independence of intensive variables when only one phase is present, allowing for varied temperatures and pressures.
The concept of the triple point, where solid, liquid, and gas phases coexist at a specific pressure and temperature.
Final summary of the Gibbs phase rule, emphasizing its utility in understanding phase changes and system states.
Invitation for viewers to ask questions and engage with the content, encouraging further exploration of the topic.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: