Understanding Circular Motion
TLDRThis educational video explores the physics of circular motion, starting with an example of spinning a ball on a rope. It explains that the ball's velocity is always tangential to the circle, and its constant change in direction means it's always accelerating. The force causing this acceleration is the centripetal force, which always points towards the center of the circle. The video clarifies the difference between centripetal force and the perceived centrifugal force, emphasizing that the latter is not a real force. It also covers the mathematical relationship between centripetal force, mass, velocity, and radius, and provides examples of circular motion in nature and human activities, such as the moon orbiting Earth and cars navigating banked roads.
Takeaways
- 🎯 The concept of circular motion involves an object moving in a circle with its velocity always tangent to the circle.
- 🏃♂️ In circular motion, even if the speed is constant, the velocity is constantly changing due to the continuous change in direction.
- 🔍 The force causing the change in direction is called centripetal force, which always points towards the center of the circle.
- 🤔 Centripetal force is not necessarily provided by a physical connection like a rope; it can also be the result of other forces such as gravity or friction.
- 🌐 The centripetal force is perpendicular to the velocity vector, maintaining the object in circular motion at a right angle to its direction of motion.
- 🚀 Centripetal force is responsible for the continuous change in direction of the velocity, which is essential for circular motion.
- 🔄 The absence of centripetal force would result in the object moving in a straight line tangent to the circle, following Newton's first law of motion.
- 🌌 The gravitational force between the Earth and the Moon is an example of centripetal force causing the Moon to orbit the Earth.
- 🛣️ When a car turns on a road, the friction between the tires and the road surface provides the necessary centripetal force to keep the car in circular motion.
- 📚 Banking a road improves the centripetal force by allowing the combination of gravitational force and the normal force from the inclined surface to contribute to the force towards the center of the circle.
Q & A
What is the primary characteristic of an object undergoing circular motion?
-The primary characteristic of an object undergoing circular motion is that its velocity is always tangent to the circle at any point in its path.
Why is the velocity of an object in circular motion considered to be constantly changing?
-The velocity of an object in circular motion is considered to be constantly changing because, although the speed (magnitude of velocity) might be constant, the direction of the velocity is continuously changing due to the circular path.
What is the term used to describe the force that causes an object to change its direction in circular motion?
-The term used to describe the force that causes an object to change its direction in circular motion is centripetal force.
What is the direction of the centripetal force relative to the velocity of the object in circular motion?
-The centripetal force is always directed towards the center of the circle, and it is always at a right angle (90 degrees) to the velocity of the object.
Can centripetal force be exerted by something other than a string or rope?
-Yes, centripetal force can be exerted by other means, such as the force of the walls in a spinning amusement park ride, which pushes riders towards the center.
What is the difference between centripetal force and the apparent centrifugal force?
-Centripetal force is a real force that acts towards the center of the circular path, while the apparent centrifugal force is not a real force; it is a sensation experienced by an object in rotational motion, which feels like it is being pushed outward due to the lack of an inward force.
What would happen if the centripetal force acting on an object in circular motion were to suddenly disappear?
-If the centripetal force were to suddenly disappear, the object would no longer be pulled towards the center and would instead continue to move in a straight line at a tangent to the circle.
What is the mathematical formula that relates centripetal force, mass, velocity, and radius in circular motion?
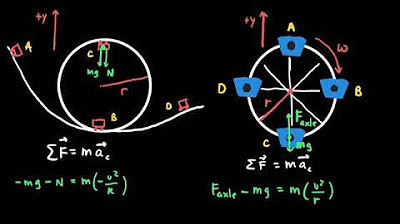
-The mathematical formula that relates centripetal force (Fc), mass (m), velocity (v), and radius (R) in circular motion is Fc = m * (v^2) / R.
How does the banking of a road affect the forces acting on a car going around a corner?
-Banking a road increases the normal force component that acts towards the center of the circle, which, combined with frictional forces, provides a greater centripetal force, allowing the car to take the corner at higher speeds without losing grip.
Why is it important for a car to have friction when going around a corner?
-Friction is important because it provides the necessary centripetal force to keep the car moving in a circular path around the corner. Without friction, the car would not be able to turn and would continue in a straight line, potentially leading to accidents.
What is the role of gravity in the circular motion of celestial bodies, such as the Moon orbiting the Earth?
-Gravity plays a crucial role as it provides the centripetal force needed to keep celestial bodies like the Moon in orbit around the Earth. The gravitational force acts as the inward pull that prevents the Moon from moving in a straight line and keeps it in its circular path.
Outlines
🎯 Introduction to Circular Motion
The video begins with an introduction to circular motion, using the example of spinning an object around one's head with a rope. The presenter explains that the object, such as a ball, moves in a circle with its velocity always tangential to the circle. The velocity is a vector quantity, meaning it has both magnitude and direction, which changes as the ball turns. This change in velocity implies acceleration, and the net force causing this is the centripetal force, exerted by the string. The force is always directed towards the center of the circle, and it's responsible for the continuous change in the direction of the velocity. The angle between the velocity vector and the force vector is always 90 degrees, defining circular motion. The video also clarifies that centripetal force is not the same as the often misunderstood centrifugal force.
🌀 Understanding Centripetal Force and Its Effects
This paragraph delves deeper into the concept of centripetal force, which is the force that keeps an object moving in a circular path. The presenter uses the example of a person in a spinning amusement park ride to illustrate that even without a string, the force exerted by the walls can cause circular motion. The force experienced by the person is inward, towards the center, and is perpendicular to their velocity. The video clarifies that the sensation of being 'flung out' is due to the rotational frame of reference and not due to a centrifugal force, which does not exist as a real force. The presenter emphasizes the importance of distinguishing between centripetal force and the perceived centrifugal force, and explains the relationship between velocity, force, and radius in circular motion.
🚀 Examples of Circular Motion in Nature and Everyday Life
The script presents examples of circular motion, such as the moon orbiting the Earth due to gravitational force, which acts as the centripetal force. Another example is a car going around a track, where the friction between the tires and the road surface provides the necessary centripetal force to keep the car on its circular path. The importance of road banking in allowing cars to take corners at higher speeds is also discussed, as it enhances the centripetal force by combining the normal force from the inclined road and the gravitational force, resulting in a net force towards the center of the circle. The video explains how banking improves the ability of a car to navigate turns by increasing the centripetal force.
📚 Conclusion and Future Exploration of Circular Motion
The video concludes with a brief mention of future content, promising mathematical examples and further exploration of centripetal forces and circular motion in upcoming videos. The presenter, Paul from High School Physics Explained, thanks the viewers for watching and encourages them to like, share, and subscribe for more educational content.
Mindmap
Keywords
💡Circular Motion
💡Velocity
💡Acceleration
💡Centripetal Force
💡Tangential
💡Centrifugal Force
💡Gravitational Force
💡Friction
💡Banking of Roads
💡Newton's First Law
Highlights
Introduction to circular motion and its basic concept.
Demonstration of spinning an object around the head with a rope to illustrate circular motion.
Explanation of the ball's velocity being tangent to the circle during circular motion.
Clarification that velocity is a vector quantity with constant magnitude but changing direction in uniform circular motion.
Description of acceleration as a change in velocity over time, including its direction.
Identification of the centripetal force as the net force causing an object to change direction in circular motion.
Visualization of the centripetal force pointing towards the center of the circle and its constant direction change.
The angle between velocity and force in circular motion is always 90 degrees.
Differentiation between centripetal force and the often misunderstood centrifugal force.
Example of circular motion in an amusement park ride without the need for a rope.
Explanation of the sensation of being flung outward in circular motion due to the rotational frame of reference.
Clarification that the outward sensation is not due to a real force but rather the result of the object's inertia.
Introduction of the formula relating centripetal force, mass, velocity, and radius (Fc = mv^2/R).
Discussion on how increasing velocity or decreasing radius increases centripetal acceleration.
Examples of circular motion in nature and human-made structures, such as the Moon orbiting Earth and cars on a track.
Explanation of gravitational force as the centripetal force causing the Moon's circular orbit around Earth.
Importance of friction as the force causing a car to turn while moving in a circular path on a track.
Discussion on the benefits of banking roads to improve a car's ability to turn at higher speeds.
Illustration of how banking roads create a net force towards the center of the circle, aiding in circular motion.
Upcoming mathematical examples in a future video to further explain centripetal forces and circular motion.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: