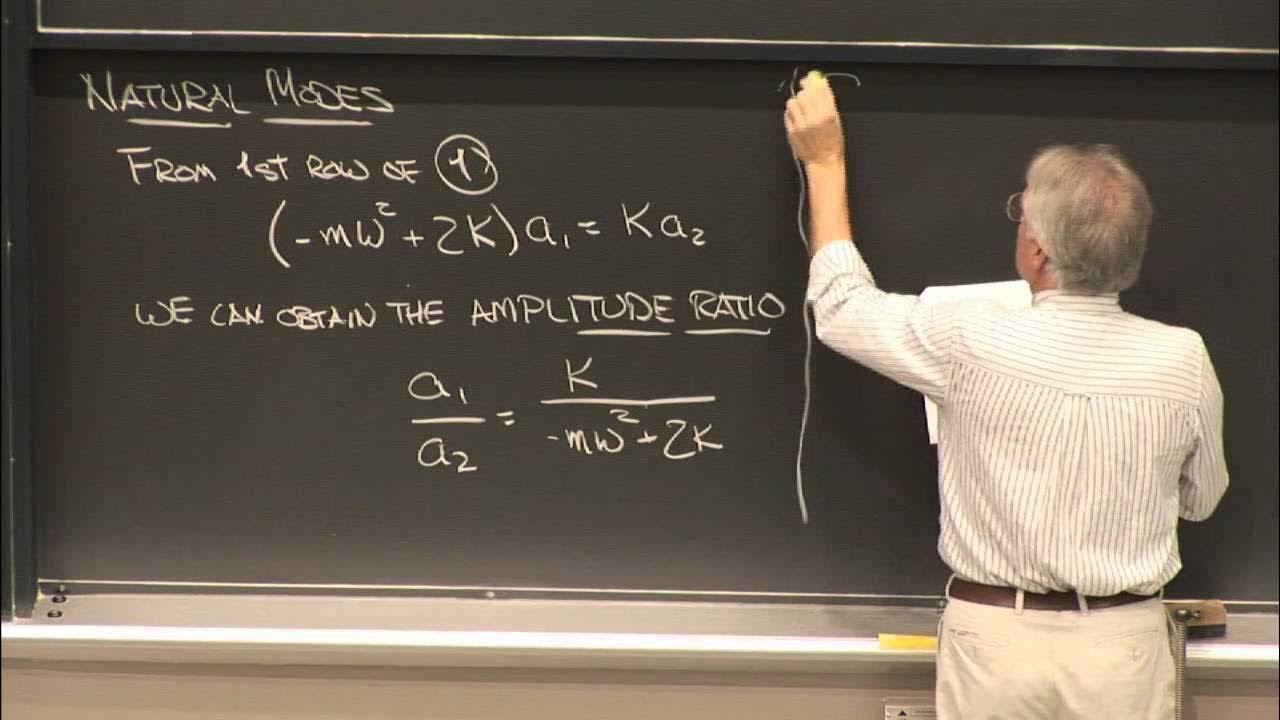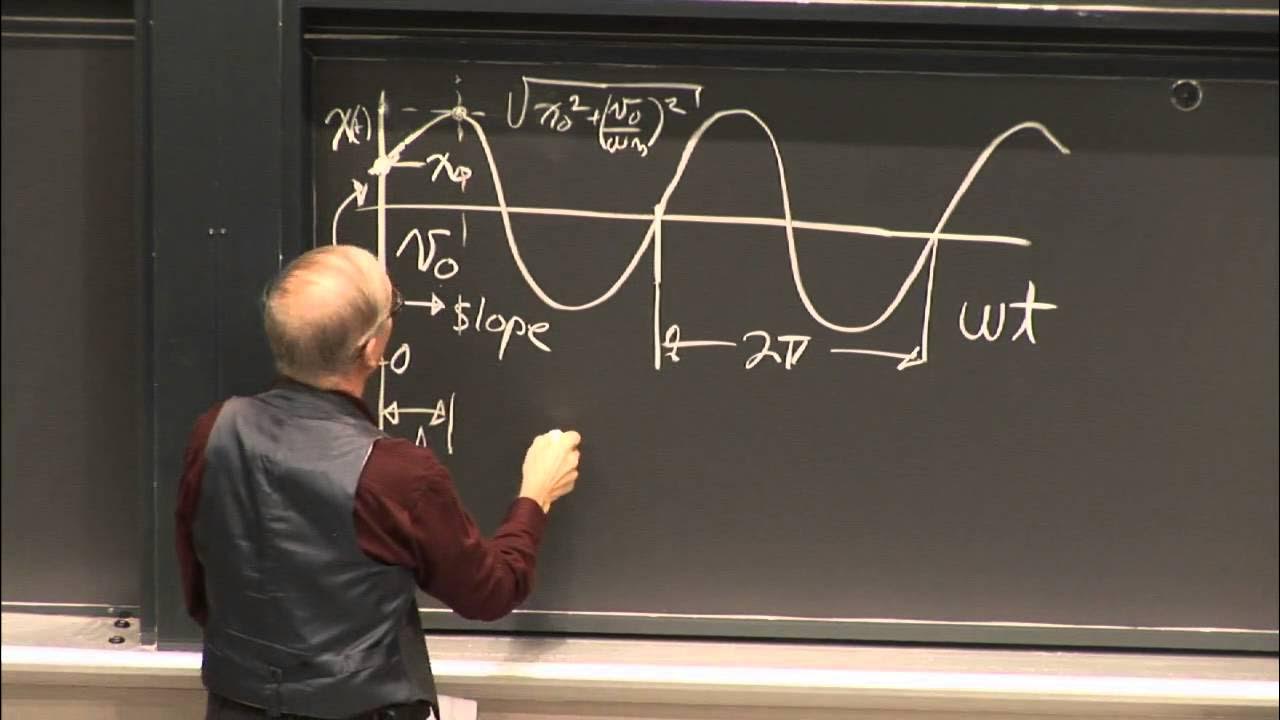24. Modal Analysis: Orthogonality, Mass Stiffness, Damping Matrix
TLDRThis lecture introduces modal analysis, a technique for studying structural vibrations by examining individual natural modes. The professor explains the concept of modeling vibrations as a sum of mode contributions, each with a distinct mode shape and natural frequency. Through examples, including a two-degree-of-freedom system, the lecture demonstrates how modal analysis simplifies the understanding and analysis of complex vibrating systems, even with continuous systems like strings or beams. The discussion also covers the challenges of damping and the use of Rayleigh damping to approximate it, providing a powerful tool for engineers to predict and control vibrations.
Takeaways
- 📚 The lecture introduces modal analysis, a technique for analyzing vibrating systems by considering their individual natural modes one at a time.
- 🌐 Modal analysis is applicable to both continuous systems like strings or beams and finite degree of freedom rigid body systems.
- 📉 The concept of natural modes involves modeling structural vibrations as a summation of individual mode contributions, each with its own mode shape and time-dependent behavior.
- 📝 The equations of motion for finite degree of freedom systems are presented, highlighting the relationship between mass, damping, stiffness matrices, and external forces.
- 🌌 The modal expansion theorem is discussed, which asserts that any motion can be represented as a superposition of contributing modes, each with its mode shape and natural coordinates.
- 🎸 A demonstration using a guitar string illustrates the different mode shapes and their corresponding frequencies for a vibrating string.
- 🔍 The lecture explains how to transform the equations of motion using mode shapes to obtain a set of decoupled single degree of freedom equations, simplifying the analysis.
- 🏗️ An example of the Hancock building is given to show the practical application of modal analysis in understanding the vibration of large structures.
- 📈 The process of finding natural frequencies and mode shapes is outlined, including the use of determinants and algebraic solutions.
- ⚙️ The importance of carrying significant digits in modal analysis calculations is emphasized for accuracy in natural frequencies and mode shapes.
- 🔨 The lecture concludes with a discussion on handling damping in modal analysis, introducing the concept of Rayleigh damping as a method to approximate damping in a system.
Q & A
What is modal analysis?
-Modal analysis is a technique used to analyze vibrating systems by considering their individual natural modes of vibration one at a time. It helps in understanding the structural vibration and provides insight into the behavior of the system when subjected to various excitations.
Why is understanding modal analysis important even if one might not perform the actual calculations throughout their career?
-Understanding modal analysis conceptually helps in having a better grasp of what vibration is all about. It offers insights that might not be otherwise apparent, enhancing the overall comprehension of a system's response to vibration.
What is the basic concept of modeling structural vibrations according to the script?
-The basic concept is that any structural vibration can be modeled as the summation of the individual contributions of each natural mode. This applies to both continuous systems like vibrating strings or beams and finite degree of freedom rigid body systems.
What are the equations of motion for finite degree of freedom systems generally written as?
-The equations of motion for finite degree of freedom systems are generally written as a mass matrix times an acceleration vector, plus a damping matrix times a velocity vector, plus a stiffness matrix times a displacement vector, all equal to an external vector of excitations.
What is the modal expansion theorem?
-The modal expansion theorem is the assertion that any motion can be represented as the superposition of each contributing mode. Each mode has a mode shape and a time-dependent behavior, often referred to as natural coordinates in textbooks.
What are mode shapes and how are they represented in the context of modal analysis?
-Mode shapes are the patterns of motion for each natural mode of a system. They are represented as vectors (u) with a superscript indicating the mode number, multiplied by their time-dependent behavior, which describes the amplitude and time dependence of each mode's contribution to the motion.
How does the orthogonality of mode shapes affect the matrices in modal analysis?
-The orthogonality of mode shapes ensures that when the mode shape matrix is pre-multiplied by the mass and stiffness matrices, the resulting matrices are diagonal. This simplifies the equations of motion into a set of independent single degree of freedom oscillators.
What is the significance of the natural frequencies and mode shapes in modal analysis?
-Natural frequencies and mode shapes are crucial in modal analysis as they describe the inherent vibrational characteristics of a system. They allow for the system's motion to be represented as a combination of these natural modes, each with its own frequency and shape, making it easier to analyze and understand the system's response to various inputs.
How can the response of a system to initial conditions be determined using modal analysis?
-The response to initial conditions can be determined by first transforming the initial conditions from the original generalized coordinates to the modal coordinates using the inverse of the mode shape matrix. Then, the response of each mode to its initial conditions is calculated independently using the equations of motion for a single degree of freedom system. Finally, the total response is obtained by summing the contributions of all relevant modes.
What is the challenge with damping in the context of modal analysis?
-The challenge with damping in modal analysis is that the damping matrix does not always diagonalize when pre-multiplied by the mode shape matrix. This can lead to off-diagonal terms that couple the modes, complicating the analysis. However, for lightly damped systems, these off-diagonal terms can often be ignored for the first-order behavior of the system.
What is Rayleigh damping and how is it used in modal analysis?
-Rayleigh damping is a model that approximates the damping matrix as a linear combination of the mass and stiffness matrices, scaled by constants alpha and beta. This model guarantees a diagonalized damping matrix, providing a way to fit the damping ratios for the modes, although it may not perfectly match all modes in a multi-degree system.
Outlines
📚 Introduction to Modal Analysis
The script begins with an introduction to modal analysis, a technique for examining vibrating systems by considering their individual natural modes. The professor emphasizes the importance of understanding this concept for gaining insight into vibration behavior. The basic idea is to model structural vibrations as a sum of individual natural modes, which applies to both continuous systems like strings or beams and finite degree of freedom rigid body systems. The equations of motion for finite degree of freedom systems are discussed, highlighting the role of mass, damping, and stiffness matrices.
🌉 Modal Expansion Theorem and System Response
The professor explains the modal expansion theorem, which allows the representation of any motion as a superposition of contributing modes, each with its mode shape and time-dependent behavior. This concept is applicable to both vibrating systems and systems with finite degrees of freedom. The script illustrates the process of representing the total system response as a combination of natural modes and discusses the implications of this for systems that vibrate, such as the example of a guitar string's different modes of vibration.
🔍 Exploring Mode Shapes and Natural Frequencies
This paragraph delves into the specifics of mode shapes and natural frequencies, using the example of a two-degree-of-freedom system with two lump masses and springs. The professor demonstrates how a system can vibrate in different modes and how the mode shapes are defined by the ratio of movements of the masses. The script also covers how to mathematically solve for these mode shapes and frequencies, highlighting the orthogonality of mode shapes, which is key to the simplification of the equations of motion.
📐 Transformation to Modal Coordinates
The script explains how to transform the equations of motion into modal coordinates, which simplifies the analysis by decoupling the system into independent single-degree-of-freedom oscillators. The process involves pre-multiplying the equations by the transpose of the mode shape matrix (u transpose), resulting in a diagonal mass and stiffness matrix. This transformation is crucial for understanding how the system responds to external forces and for deriving the natural coordinates or modal coordinates.
🏗️ Application of Modal Analysis to Complex Systems
The professor discusses the practical applications of modal analysis, particularly in the context of complex systems such as buildings. Using the example of the Hancock building, the script illustrates how modal analysis can provide a simplified model of a system with many possible natural modes, allowing engineers to predict and understand the behavior of such systems under different conditions.
🔧 Response to Initial Conditions and Damping
The script addresses how to calculate the response of a system to initial conditions using modal analysis. It explains the process of determining the initial conditions in modal coordinates and the importance of carrying significant digits for accuracy. The professor also introduces the concept of damping in the system and its impact on the response, noting that the damping matrix may not always be diagonal, which can complicate the analysis.
📉 Dealing with Damping in Modal Analysis
This paragraph focuses on the challenges of incorporating damping into the modal analysis. The professor explains that while the mass and stiffness matrices are symmetric and can be easily diagonalized, the damping matrix is more complex. The script introduces Rayleigh damping, a method that allows for the approximation of a diagonal damping matrix by adjusting two parameters, alpha and beta, which can be used to fit the damping ratios of the system's modes.
🔄 Calculation of Initial Conditions in Modal Coordinates
The script provides a step-by-step explanation of how to calculate initial conditions in modal coordinates. It describes the process of using the inverse of the mode shape matrix to transform initial displacements and velocities from the original generalized coordinates to the modal coordinates, which is essential for solving the system's response to initial conditions.
📝 Example Calculations and Inverse Mode Shape Matrix
The professor concludes the script with example calculations of initial conditions for a system with given initial displacements. The script demonstrates the computation of the inverse mode shape matrix and its use in determining the initial modal displacements and velocities. This practical application reinforces the concepts discussed throughout the script and provides a clear example of how modal analysis is applied in practice.
Mindmap
Keywords
💡Modal Analysis
💡Natural Modes
💡Mode Shape
💡Vibration
💡Equations of Motion
💡Generalized Coordinates
💡Orthogonality
💡Damping
💡Rayleigh Damping
💡Initial Conditions
💡Transient Response
Highlights
Introduction to modal analysis, a technique for analyzing vibrating systems by considering them one mode at a time.
Modal analysis provides a conceptual understanding of vibration, offering insights that can be applied to various careers in engineering.
Structural vibrations can be modeled as a summation of individual natural modes, applicable to both continuous and finite degree of freedom systems.
Equations of motion for finite degree of freedom systems are presented, including mass, damping, and stiffness matrices.
The modal expansion theorem is introduced, allowing any motion to be represented as a superposition of contributing modes.
Mode shapes and natural coordinates are defined, illustrating how they contribute to the system's motion.
A demonstration of a guitar string's mode shapes and their corresponding frequencies is provided.
Explanation of how mode shapes for a two-degree-of-freedom system are determined and their significance in understanding system dynamics.
The process of transforming the equations of motion using modal analysis to obtain a diagonalized form, simplifying the system to independent single degree of freedom equations.
Orthogonality of mode shapes is discussed, explaining why the mass and stiffness matrices become diagonal when pre-multiplied by the mode shape matrix.
The concept of modal mass and how it relates to the natural frequency of each mode is introduced.
A historical case study of the Hancock building's window failures is presented to illustrate the practical application of modal analysis.
The method to calculate the response of a system to initial conditions using modal coordinates is explained.
An example of how to revert from modal coordinates to generalized coordinates to understand the physical motion of the system.
Discussion on the complexities of modeling damping in a system and the approximations made to simplify the analysis.
Rayleigh damping is introduced as a method to model damping in a system, allowing for a diagonalized damping matrix.
A step-by-step guide on how to calculate initial conditions in modal coordinates and apply them to the equations of motion.
The importance of carrying significant digits in modal analysis to ensure accurate results is emphasized.
Final thoughts on the power of modal analysis in providing immediate insight into the behavior of vibrating systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: