Understanding Vibration and Resonance
TLDRThis video delves into the critical role of understanding vibrations in engineering, showcasing how mass-spring models are used to analyze and predict the behavior of structures under various conditions. It covers the dynamics of single degree-of-freedom systems, introduces natural frequency and damping, and explores scenarios like forced vibration and resonance. The script also touches on more complex multi-degree-of-freedom systems and the challenges of seismic design, offering viewers a comprehensive insight into the world of vibrations and their impact on engineering applications.
Takeaways
- 🏗️ Vibration analysis is crucial for engineering applications like building machinery, launching instruments into space, and designing buildings in seismic areas.
- 📐 Engineers simplify complex systems by using lumped parameter models, which combine all mass and stiffness into a single point mass and spring model for easier analysis.
- 🔍 The single degree-of-freedom model is a simplified representation that assumes only vertical movement and no damping, making it easier to analyze mathematically.
- 📉 Newton's second law (F=ma) is used to derive the equation of motion for a vibrating system, leading to a sinusoidal function solution for the displacement over time.
- 🌀 The natural frequency of a system, represented by the Greek letter Omega, is a key property that dictates how it will oscillate in free vibration and is determined by mass and stiffness.
- 📏 Damping, the loss of energy during oscillation, is a critical factor in real-world systems and can be modeled using a dashpot, which introduces a damping force proportional to velocity.
- 🔄 Damping can lead to different types of system responses: underdamped (decreasing oscillations), overdamped (no oscillations), and critically damped (minimal oscillation for quick settling).
- 📊 The damping ratio, derived from the logarithmic decrement, helps in understanding the overall damping in a system and is essential for accurate modeling.
- 🔨 Forced vibration, driven by external forces like unbalance in rotating machinery, can be analyzed by adding a sinusoidal external load to the spring-mass model.
- 📈 The steady-state response of a system during forced vibration aligns with the frequency of the external force but is phase-shifted, and can lead to resonance if the forcing frequency matches the natural frequency.
- 🌉 Resonance, where the system's amplitude increases significantly, is a critical phenomenon that needs careful assessment, especially in structures like bridges that could be affected by matching natural and forcing frequencies.
Q & A
Why is understanding the behavior of vibrating structures important for engineers?
-Understanding the behavior of vibrating structures is crucial for engineers as it enables them to build rotating machinery, launch sensitive instruments into space, and design buildings in seismic areas safely, among other applications.
What is the lumped parameter modeling approach in the context of vibrating systems?
-The lumped parameter modeling approach is a common method used by engineers to simplify complex vibrating systems. It involves combining all contributions to mass and stiffness into a single point mass with mass 'm' and a spring with stiffness 'k', making it easier to analyze the system's dynamics.
What are the two most important parameters in any vibrating system?
-The two most important parameters in any vibrating system are its mass and its stiffness, as these determine the system's dynamic behavior.
What is a single degree-of-freedom model, and why is it used?
-A single degree-of-freedom model is a simplified model that assumes the mass can only move in one direction, typically up and down. It is used because it allows for the analysis of the system's behavior in a more straightforward manner, focusing on a single output, the x coordinate of the mass.
Why do engineers initially neglect the effects of gravity and damping when building a vibrating system model?
-Engineers initially neglect the effects of gravity and damping to simplify the model and focus on understanding the system's free vibration behavior. This simplification helps in deriving the fundamental dynamics of the system before considering more complex factors.
What is the equation of motion for a vibrating system, and how is it derived?
-The equation of motion for a vibrating system is derived by applying Newton's second law, F=ma, which states that the sum of the forces acting on the point mass is equal to the product of its mass and its acceleration. In the case of a mass-spring system, the only force acting is the spring force, leading to an ordinary differential equation that describes the system's motion.
How is the amplitude of vibration determined in a mass-spring system?
-The amplitude of vibration in a mass-spring system is determined by considering the initial position and velocity of the mass. By differentiating the equation for displacement 'x' with respect to time, the amplitude 'A' can be calculated.
What is the natural frequency of a system, and how is it calculated?
-The natural frequency of a system is the frequency at which it will oscillate naturally when in free vibration. It is calculated from the solution to the equation of motion and is denoted by the Greek letter 'Omega'. It depends only on the mass and the spring stiffness.
What is damping, and why is it important to consider it in real mechanical systems?
-Damping is the loss of energy from a vibrating system as it oscillates, often due to friction or other means. It is important to consider damping in real mechanical systems because energy is always dissipated as heat over time, causing the oscillations to decrease in magnitude and eventually stop.
What are the different types of damping mechanisms that can contribute to a system's overall damping?
-Different types of damping mechanisms include structural damping, where energy is dissipated due to the relative motion of components at structural joints, and material damping, which is provided by the material itself as energy dissipates due to molecular-level interactions during vibration.
How does the concept of resonance relate to the natural frequency and forcing frequency of a system?
-Resonance occurs when the frequency of the external forcing load is very close to the natural frequency of the system. In this case, the energy added by the external force is timed to increase the amplitude of the displacement with each cycle, potentially leading to large displacements and potentially dangerous situations.
What is a tuned mass damper, and why is it used in structures like buildings and bridges?
-A tuned mass damper is a device installed in structures like buildings and bridges to control the dynamic response at resonant frequencies. It helps to mitigate the effects of resonance, which can be dangerous if the natural frequency of the structure matches the frequency of external forces, such as wind or seismic activity.
How does the equation of motion for a system with multiple degrees of freedom differ from a single degree-of-freedom system?
-For a system with multiple degrees of freedom, each mass in the model has its own equation of motion. When rewritten in matrix form, the system of equations maintains the same form as the equation of motion for a single degree-of-freedom system, but with additional terms to account for the interactions between the different masses.
What are mode shapes, and how do they relate to the natural frequencies of a system?
-Mode shapes are the specific ways in which a system with multiple degrees of freedom vibrates at each of its natural frequencies. Each natural frequency corresponds to a unique mode shape, describing the pattern of motion for the system during vibration.
Why might engineers use numerical techniques like the finite element method for systems with many degrees of freedom?
-As the number of degrees of freedom in a system increases, it becomes necessary to use numerical techniques like the finite element method to determine the natural frequencies and associated mode shapes. These techniques allow for the analysis of complex systems that cannot be easily solved analytically.
Outlines
🔍 Fundamentals of Vibration Analysis
This paragraph introduces the importance of understanding structural vibrations in various engineering applications, such as building machinery, launching instruments into space, and designing buildings in seismic areas. It explains the concept of lumped parameter modeling, which simplifies a complex system into a point mass (m) and a spring (k) to study its dynamics. The paragraph also outlines the assumptions made in a single degree-of-freedom model, such as ignoring gravity, damping, and external loads, and focuses on free vibration. The equation of motion is derived using Newton's second law, leading to a sinusoidal solution for the system's vibration, which can be analyzed further with given initial conditions.
📏 Exploring Damping and Natural Frequency
The second paragraph delves into the effects of damping on a vibrating system, which is the energy loss over time due to factors like friction. It describes different types of damping, such as structural and material damping, and introduces the concept of a dashpot as a simplified model for damping. The paragraph explains how damping can be represented mathematically in the equation of motion and the resulting behavior of underdamped, overdamped, and critically damped systems. It also discusses how to determine the damping coefficient experimentally using the logarithmic decrement and the damping ratio, which is crucial for modeling real-world systems.
🔨 Forced Vibration and Resonance
This section examines forced vibration, which occurs when an external force drives the oscillation of a system, such as unbalanced rotating machinery. The paragraph explains how to analyze forced vibration using a spring-dashpot model with an external sinusoidal load, resulting in a non-homogeneous differential equation. It discusses the complementary and particular solutions to this equation and how the system's response, especially the steady-state response, is influenced by the external force's frequency. The concept of resonance is introduced, where the system's amplitude becomes very large when the forcing frequency matches the natural frequency, potentially leading to dangerous situations.
🏢 Advanced Modeling with Multiple Degrees of Freedom
The final paragraph discusses the limitations of single degree-of-freedom models and the need for multiple degrees of freedom in more complex systems, such as a three-story building. It explains how each degree of freedom has its own natural frequency and mode shape, and how these can be determined using matrix form equations or numerical techniques like the finite element method. The paragraph also touches on other types of vibrations, such as pendulums, and mentions a companion video on Nebula for further exploration. Lastly, it promotes a streaming service partnership between Nebula and Curiosity Stream, offering a discount and highlighting the educational value of their content.
Mindmap
Keywords
💡Vibration
💡Engineers
💡Lumped Parameter Modelling
💡Mass
💡Stiffness
💡Single Degree-of-Freedom Model
💡Damping
💡Natural Frequency
💡Resonance
💡Tuned Mass Damper
💡Degrees of Freedom
💡Mode Shape
Highlights
Engineers use simplified models to study the vibrating behavior of complex systems, focusing on mass and stiffness as key parameters.
The lumped parameter modeling approach simplifies systems by representing them with a point mass and spring, allowing for mathematical analysis.
A single degree-of-freedom model assumes mass movement in one direction, ignoring gravity and damping for initial analysis.
Newton's second law is applied to derive the equation of motion for a vibrating system, leading to sinusoidal solutions.
The amplitude and phase angle of vibration can be determined from initial conditions, such as position and velocity.
The natural frequency of a system, denoted by Omega, is a key property derived from the mass-spring model.
Natural frequency can also be expressed in Hertz, and its inverse, the period T, measures the cycle duration in seconds.
Different systems with varying masses and stiffnesses have distinct natural frequencies, affecting their oscillation rates.
Tuning forks demonstrate natural frequency through their vibration, producing tones at specific frequencies.
Damping, the energy loss in a system, is a crucial factor in real-world applications and is often modeled using a dashpot.
Viscous damping is a common model that represents damping forces proportional to the velocity of displacement.
Damping affects the equation of motion, leading to different responses like underdamped, overdamped, and critically damped systems.
The damping ratio is a critical parameter in understanding a system's response to damping, usually determined experimentally.
Forced vibration occurs when an external force drives the oscillation, such as in rotating machinery with unbalance.
Resonance, a dangerous phenomenon where displacement becomes very large, occurs when forcing frequency matches the natural frequency.
Tuned mass dampers are used in structures like buildings and bridges to mitigate the effects of resonance during seismic events.
Multiple degree-of-freedom models, such as those for a three-story building, can capture more complex dynamic responses.
Numerical techniques and methods like the finite element method are essential for analyzing systems with higher degrees of freedom.
The video also covers pendulum motion and its differences from mass-spring systems in a companion video on Nebula.
Curiosity Stream and Nebula offer a streaming bundle with a discount, supporting educational content creators.
Transcripts
Browse More Related Video
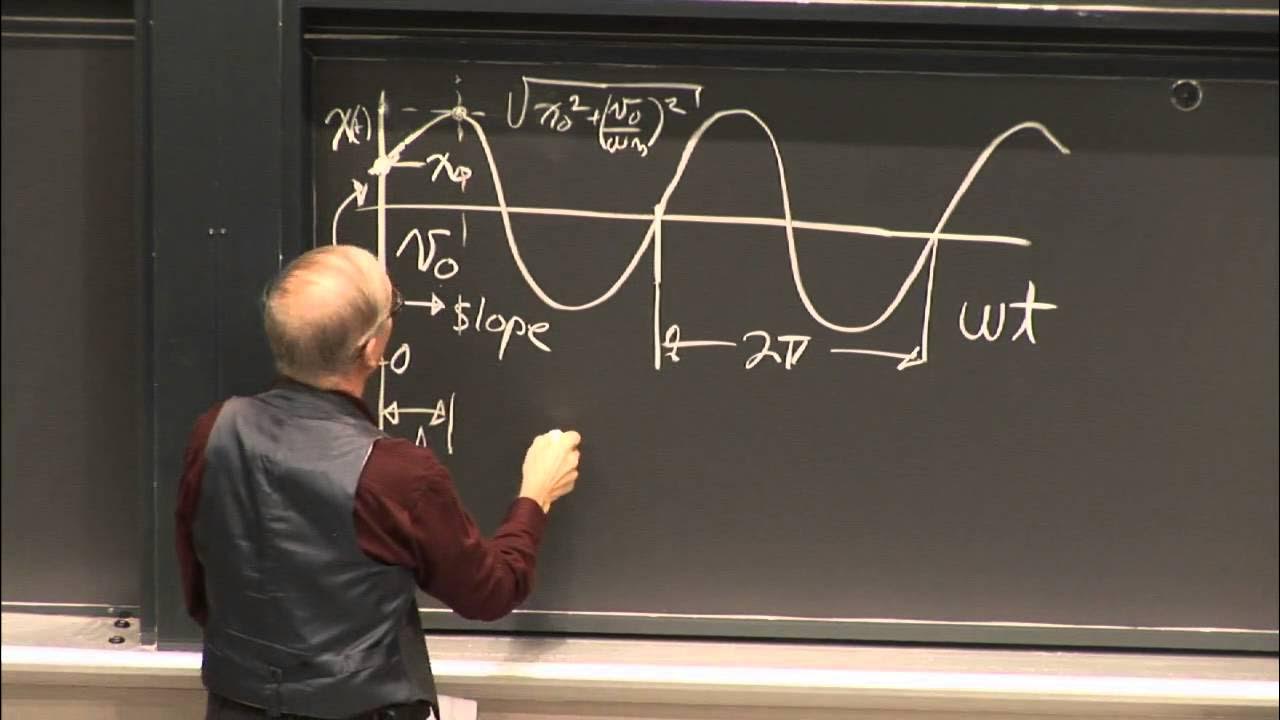
19. Introduction to Mechanical Vibration
24. Modal Analysis: Orthogonality, Mass Stiffness, Damping Matrix

High School Physics - Resonance
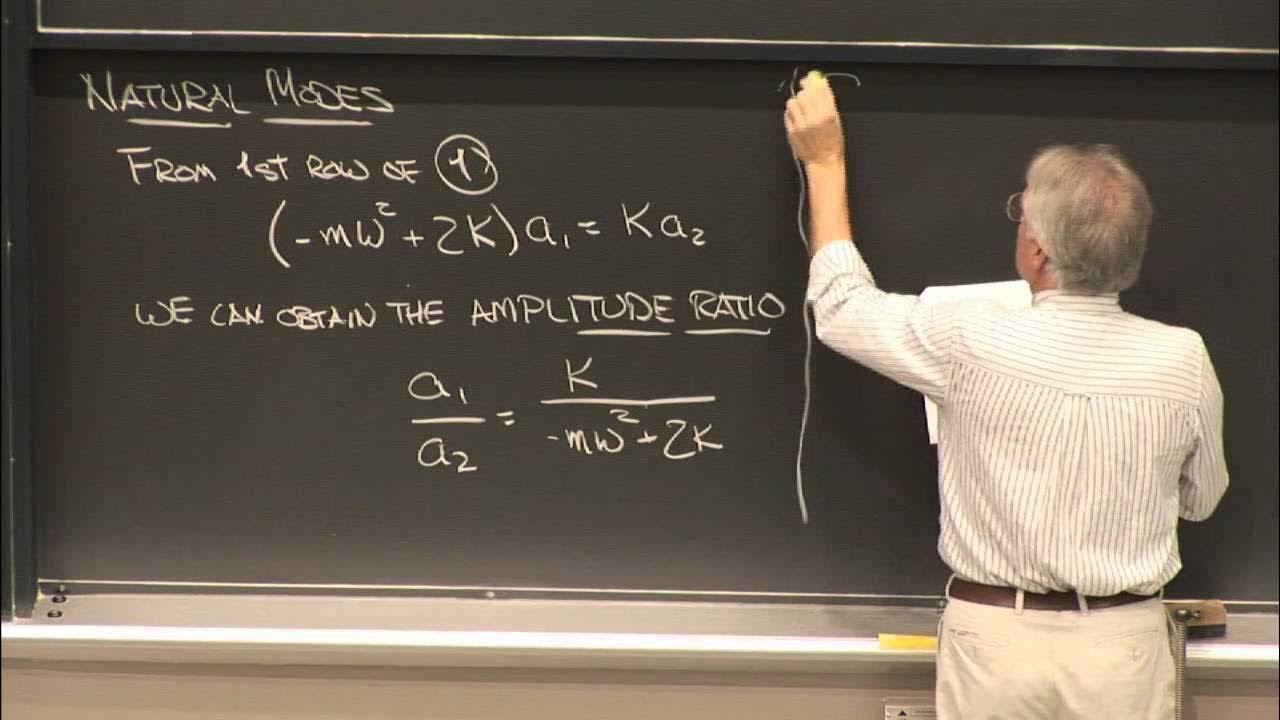
22. Finding Natural Frequencies & Mode Shapes of a 2 DOF System
Simple Harmonic Motion - Springs in series vs parallel, and vertical springs

Water System | One-Component System | Phase Rule | Applied Chemistry 1 | B Tech | GGSIPU
5.0 / 5 (0 votes)
Thanks for rating: