Introduction to Degrees of Freedom

LearnChemE
3 Sept 201408:33
EducationalLearning
32 Likes 10 Comments

TLDRThis screencast offers an insightful overview of degree of freedom analysis, a fundamental tool in engineering problem-solving. It explains the concept by comparing algebraic systems with varying numbers of equations and unknowns, illustrating underspecified, properly specified, and overspecified scenarios. The video then applies this concept to chemical process modeling, emphasizing the importance of balancing the number of unknowns with independent equations derived from material balances, process specifications, and physical property data. Through two examples, it demonstrates how to calculate degrees of freedom and the significance of having zero degrees of freedom for solvable problems, highlighting the method's utility in complex process analysis.

Takeaways
  • 🔍 Degree of freedom analysis helps determine if there's enough information to solve engineering problems.
  • 📊 When the number of unknowns is greater than the number of equations, the system is underspecified and can't be solved.
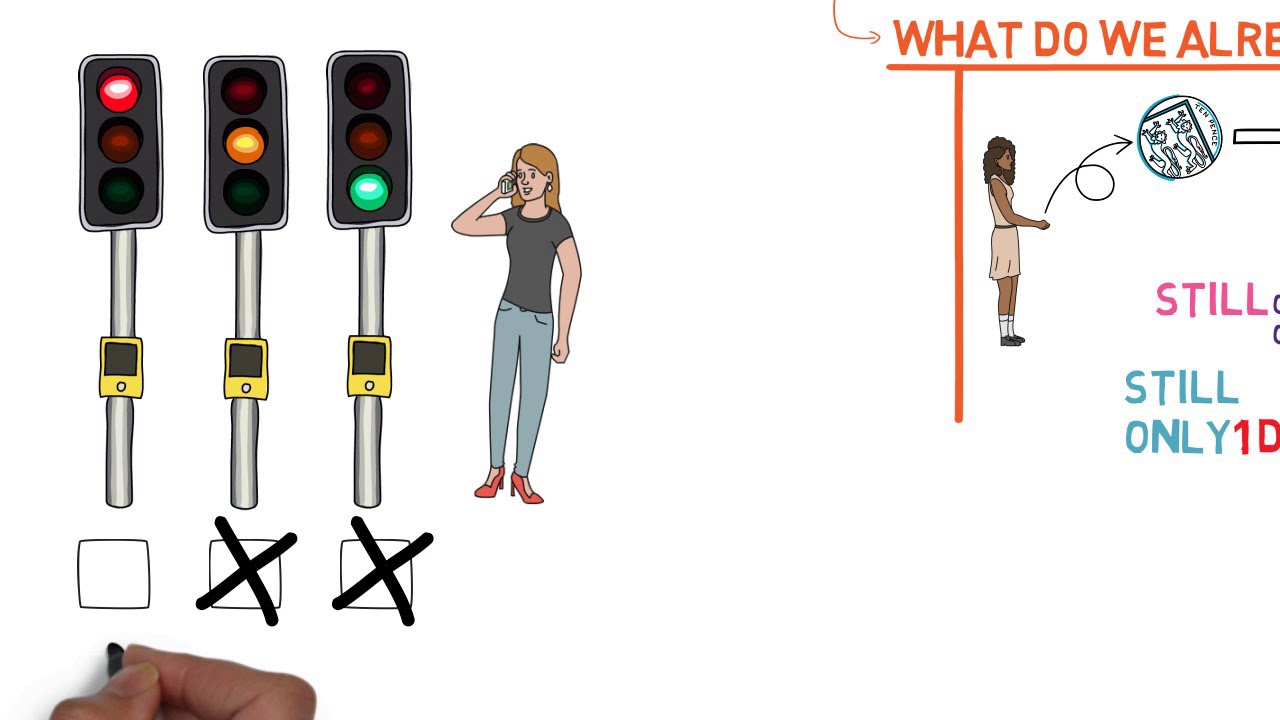
  • ⚖️ When the number of unknowns equals the number of equations, the system has zero degrees of freedom and can be solved.
  • ❌ When the number of unknowns is less than the number of equations, the system is overspecified and may yield inconsistent results.
  • 🔢 Degree of freedom analysis involves calculating the number of unknowns and subtracting the number of independent balances and other equations.
  • 🌐 Independent balances can include material balances, total balances, and other equations such as process specifications and physical properties.
  • 🔬 In engineering problems, degree of freedom analysis is crucial for modeling and analyzing processes, particularly chemical processes.
  • 📚 The number of independent material balances is equal to the number of species present in the system.
  • 🧮 Total balances are not independent from species balances; they are derived from the sum of species balances.
  • 💡 Degree of freedom analysis is essential for solving complex processes with multiple units, starting with individual systems.
Q & A

  • What is the purpose of degree of freedom analysis in engineering problems?

    -The purpose of degree of freedom analysis in engineering problems is to determine whether there is enough or too much information to solve a particular problem. It helps in identifying if the system is underspecified, overspecified, or has zero degrees of freedom, which is the ideal scenario for solving the problem.

  • How does the number of unknowns and equations relate to the degree of freedom in a system?

    -The degree of freedom is calculated by comparing the number of unknowns to the number of equations. If the number of unknowns is greater than the number of equations, the system is underspecified with a positive degree of freedom. If the number of unknowns equals the number of equations, the system has zero degrees of freedom, which is desirable. If the number of unknowns is less than the number of equations, the system is overspecified, which can lead to inconsistent results.

  • What is an underspecified system in the context of degree of freedom analysis?

    -An underspecified system is one where the number of unknowns exceeds the number of equations. In such a system, there is not enough information to solve for all the unknowns without additional equations or information.

  • What is an overspecified system in the context of degree of freedom analysis?

    -An overspecified system is one where there are more equations than unknowns. This can lead to inconsistent results or answers for the unknowns, as the equations may not be compatible with each other, preventing a single unique solution.

  • How does the concept of degrees of freedom relate to solving algebraic equations?

    -In the context of algebraic equations, the concept of degrees of freedom is analogous to determining whether a system of equations has a unique solution, no solution, or infinitely many solutions based on the number of equations and unknowns. It provides an intuitive sense of the sufficiency of information to solve the equations.

  • What is the significance of zero degrees of freedom in engineering problems?

    -Zero degrees of freedom signifies that there is a perfect balance between the number of unknowns and the number of equations. This is the ideal scenario as it indicates that there is just enough information to solve for all the unknowns, leading to a unique and consistent solution.

  • How can the number of independent balances be determined in a material balance problem?

    -The number of independent balances in a material balance problem is determined by the number of species present in the system. One can write an independent balance for each species. A total balance can also be written, but it is dependent on the individual species balances and therefore is not considered independent.

  • What are some sources of additional equations that can be used in a material balance problem besides species balances?

    -Additional equations in a material balance problem can come from process specifications, physical property data, and equilibrium equations. Process specifications might include known ratios between flow rates, while physical property data could provide information like density or specific gravity. Equilibrium equations can relate unknowns in ways that are different from mass balances.

  • What are the potential outcomes when calculating the degrees of freedom for a system?

    -There are three potential outcomes: If the degrees of freedom are equal to zero, the problem can be solved with the necessary equations to relate the unknowns. If the degrees of freedom are greater than zero, the system is underspecified and more information is needed to solve for all unknowns. If the degrees of freedom are less than zero, the system is overspecified, indicating more equations than unknowns.

  • Can you provide an example of how to apply degree of freedom analysis to a single unit process with two inputs and two outputs?

    -In a single unit process with two inputs and two outputs, you would first identify the unknowns, such as flow rates and composition variables. Then, you would determine the number of independent balances that can be written, which is equal to the number of species. If the number of unknowns equals the number of independent balances, the system has zero degrees of freedom and can be solved. Additional equations from process specifications or other relationships can also be used to reduce the degrees of freedom to zero.

  • How does the mole fraction constraint help in reducing the degrees of freedom in a material balance problem?

    -The mole fraction constraint, which states that the sum of all mole fractions must equal one, provides an additional equation that can be used to reduce the degrees of freedom. By recognizing that one composition variable can be expressed in terms of others, you effectively reduce the number of independent unknowns, bringing the system closer to having zero degrees of freedom.

Outlines
00:00
🔍 Introduction to Degree of Freedom Analysis

This paragraph introduces the concept of degree of freedom analysis, explaining its significance in engineering problem-solving. It emphasizes the need to determine if there is sufficient information to solve a problem. The explanation begins with an analogy using algebraic expressions to illustrate underspecified, well-specified, and overspecified systems. The importance of having zero degrees of freedom is highlighted, as it indicates the presence of enough information to uniquely solve for the unknowns. The paragraph also outlines how to perform a degree of freedom analysis in the context of engineering, specifically mentioning the use of material balances and other relevant equations such as process specifications, physical property data, and equilibrium equations.

05:02
📚 Application of Degree of Freedom Analysis in Material Balances

The second paragraph delves into applying degree of freedom analysis to material balances within single unit processes. It provides two examples to demonstrate the calculation and implications of degrees of freedom. The first example features a process with two inputs and two outputs, detailing how to identify three unknowns and the corresponding three independent material balances, leading to zero degrees of freedom and a solvable system. The second example presents a scenario with one input and two outputs, initially suggesting two degrees of freedom due to five unknowns and only three independent balances. However, additional information, such as a ratio relating flow rates and a composition constraint, reduces the degrees of freedom to zero, indicating a solvable system. The paragraph concludes by emphasizing the value of degree of freedom analysis in quickly assessing the solvability of problems and its increasing importance in more complex processes.

Mindmap
Keywords
💡Degree of Freedom Analysis
Degree of Freedom Analysis is a method used in engineering to determine whether there is a sufficient amount of information to solve a particular problem. It's central to the video's theme as it provides a framework for understanding the balance between the number of unknowns and the equations available to solve them. The script uses algebraic expressions to illustrate this concept, showing that an underspecified system occurs when the number of unknowns exceeds the number of equations, an overspecified system when the equations exceed the unknowns, and the ideal scenario of zero degrees of freedom where the two are equal, allowing for a solvable system.
💡Underspecified System
An underspecified system is one where the number of unknowns is greater than the number of equations available to solve them. In the context of the video, this concept is introduced through an algebraic example where one equation with two unknowns (2X + Y = 7) cannot be solved for both variables without additional information. The video emphasizes that in engineering problems, an underspecified system means more information is needed to find a solution.
💡Overspecified System
An overspecified system occurs when there are more equations than unknowns, which can lead to inconsistent results or answers for the unknowns. The script provides an example with three equations and two unknowns, leading to different solutions for the same variables when different pairs of equations are used. This highlights the importance of having a balanced number of equations and unknowns to achieve a unique and consistent solution in engineering problems.
💡Zero Degrees of Freedom
Zero degrees of freedom is the ideal state in engineering problems where the number of unknowns is equal to the number of equations, allowing for a solvable system. The video script illustrates this with an algebraic example where two equations with two unknowns can be solved simultaneously to find specific values for X and Y. This concept is crucial as it represents the goal in degree of freedom analysis—to have just enough information to solve for all unknowns.
💡Material Balance
Material balance is a fundamental concept in chemical engineering, referring to the conservation of mass principle where the total amount of a substance entering a system must equal the total amount leaving, accounting for any transformations or reactions. In the video, material balances are used to write equations that relate unknown flow rates and compositions in a process. The number of independent balances is equal to the number of species present, which is key in performing a degree of freedom analysis.
💡Independent Balances
Independent balances are equations that can be written for each species in a system without being dependent on other balances. The video explains that for a material balance, one can write an independent balance for each species, but a total balance would be dependent on the individual species balances. These independent balances are essential in calculating the degrees of freedom for a system.
💡Unknowns
Unknowns in the context of the video refer to the variables or quantities that need to be determined in an engineering problem. The script discusses how the number of unknowns, when compared to the number of equations, dictates whether a system is underspecified, overspecified, or has zero degrees of freedom. Examples from the script include unknown flow rates and composition variables in a chemical process that must be solved for using the available equations.
💡Equations
Equations in the video are the mathematical expressions used to relate unknowns in a system. They can come from various sources such as mass or energy balances, process specifications, physical property data, or equilibrium equations. The script emphasizes that the number of equations must be balanced with the number of unknowns to achieve a solvable system with zero degrees of freedom.
💡Process Specifications
Process specifications are given conditions or constraints in an engineering problem that can provide additional equations to relate unknowns. In the video, an example of process specifications is provided where the relationship or ratio between different flow rates is known, which helps in reducing the degrees of freedom in a system.
💡Physical Property Data
Physical property data refers to known characteristics of substances such as density, specific gravity, pressure, and temperature. The video script mentions that this data can be used to derive additional equations, like using the ideal gas law to determine flow rates, thereby helping in solving for unknowns in a system.
💡Equilibrium Equations
Equilibrium equations are used in chemical engineering to describe the relationships between substances at equilibrium, often involving reaction rates and concentrations. The script mentions these equations as a source of additional information that can be used to relate unknowns in a system, contributing to the overall degree of freedom analysis.
Highlights

Overview of degree of freedom analysis provided.

Explanation of degree of freedom analysis and its application in engineering problems.

Degree of freedom analysis determines if there is enough information to solve a problem.

An intuitive sense of degree of freedom analysis through algebraic expressions.

Underspecified system example with one equation and two unknowns.

Zero degrees of freedom scenario with equal number of unknowns and equations.

Overspecified system example with more equations than unknowns leading to inconsistent results.

Importance of zero degrees of freedom for solving engineering problems.

Degree of freedom analysis as the first step in chemical process modeling.

Calculation of degrees of freedom by considering unknowns and independent balances.

Material balance focus and the role of species in independent balances.

Total balance as dependent on species balances.

Other equations from process specifications, physical property data, and equilibrium equations.

Three potential outcomes of degree of freedom calculation: solvable, underspecified, or overspecified.

Application of degree of freedom analysis to material balances on single units.

Example of a single unit process with two inputs and two outputs.

Example of a single unit with one input and two outputs and its degree of freedom analysis.

Use of additional equations and constraints to solve for unknowns in underspecified systems.

Degree of freedom analysis as a powerful tool for problem-solving in complex processes.

Transcripts

Browse More Related Video

what are degrees of freedom?

Degrees Of Freedom Explained | What is Degrees of freedom | Degrees of freedom in statistics

What are degrees of freedom in statistics? A simple explanation.

Find a pvalue using a t table

Degrees of Freedom

What is a degree of freedom?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Engineering AnalysisProblem SolvingDegree of FreedomAlgebraic SystemsMaterial BalanceChemical ProcessSystem SolvingEngineering DesignEducational ContentProcess Optimization