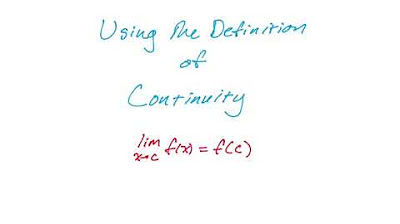Example (2.2) - Finding the limit of a function from a Graph #2 (Calc)
TLDRThe video script explains how to find limits of a piecewise function by analyzing its graph. It covers examples of finding the limit as X approaches different values, such as -4, -1, 0, and -0.7. The instructor highlights that for continuous functions, limits can be determined directly. However, in the presence of jump discontinuities, as shown in the piecewise function, the limit does not exist at certain points due to differing Y-values. This detailed walkthrough helps viewers understand the concept of limits in calculus, especially in piecewise functions with discontinuities.
Takeaways
- 📈 The script discusses finding limits of a piecewise function on a graph.
- 🔍 The function G is analyzed for its behavior as X approaches different values.
- 👉 The limit of G as X approaches negative 4 is y equals 0.
- 🚫 The limit as X approaches negative 1 is y equals negative 1.
- 💡 The limit as X approaches 0 is not straightforward due to a jump discontinuity.
- 🙅♂️ The limit at X equals 0 does not exist because the left and right limits are not equal (y equals negative 1 and y equals 1).
- 📌 The concept of a jump discontinuity is introduced as a reason for the non-existence of a limit.
- 👀 The script emphasizes the importance of checking the left and right limits to determine the existence of a limit.
- 📍 The limit as X approaches negative 0.7 is y equals negative 1, indicating continuity at this point.
- 🔑 The script highlights the difference between limits at points of continuity and discontinuity in piecewise functions.
- 📝 The overall message is to carefully analyze the behavior of functions near points of interest to determine the existence of limits.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is finding the limits of a piecewise function as X approaches different numbers.
What is a piecewise function?
-A piecewise function is a function that is defined by different expressions over different intervals or domains.
What is the limit of the function G as X approaches negative 4 according to the script?
-The limit of the function G as X approaches negative 4 is y equals 0.
What is the limit of the function G as X approaches negative 1?
-The limit of the function G as X approaches negative 1 is y equals negative 1.
Why does the limit as X approaches 0 not exist in the given function?
-The limit as X approaches 0 does not exist because the function has a jump discontinuity, with the left and right limits approaching different values (negative 1 and 1 respectively).
What is the limit of the function G as X approaches negative 0.7?
-The limit of the function G as X approaches negative 0.7 is y equals negative 1.
What is a jump discontinuity in the context of the script?
-A jump discontinuity refers to a point on the graph where the function has a sudden 'jump' or 'drop', and the left and right limits do not match, indicating the function is not continuous at that point.
How does the script illustrate the process of finding limits?
-The script illustrates the process by examining the function's behavior as X approaches specific values and noting the corresponding Y values to determine the limits.
What does the script suggest about limits at points of continuity?
-The script suggests that for a continuous function, if the function passes through a given point, you can find a limit at that point.
Why is it important to consider both left and right limits when determining if a limit exists?
-It is important to consider both left and right limits because if they do not converge to the same value, the limit does not exist at that point, indicating a discontinuity.
What does the script imply about the relationship between piecewise functions and limits?
-The script implies that piecewise functions may have points of discontinuity where limits do not exist, especially at the points where the function 'jumps' from one expression to another.
Outlines
📚 Understanding Limits of a Piecewise Function
This paragraph introduces the concept of limits in the context of a piecewise function, as demonstrated with a graph. The instructor explains how to find the limit of the function G(x) as X approaches different values. The limits are determined by observing the behavior of the function as X gets closer to specific points: negative 4, negative 1, 0, and negative 0.7. The instructor emphasizes that the limit exists when the function is continuous and approaches a single value, but does not exist when there's a jump discontinuity, as seen when X approaches 0, where the function values are both negative 1 and 1.
Mindmap
Keywords
💡Graph
💡Piecewise function
💡Limit
💡Approaches
💡Discontinuity
💡Y value
💡Continuous function
💡Jump discontinuity
💡Does not exist
💡Flat line
Highlights
Introduction to a standard beginning example from section 2.2.
Explanation of a graph with a piecewise function due to the jump cut discontinuity.
Task to find the limit of G(x) as X approaches negative 4.
Observation that the limit as X approaches negative 4 is Y equals 0.
Task to find the limit as X approaches negative 1.
Identification of the limit at X equals negative 1 as Y equals negative 1.
Task to determine the limit as X approaches 0.
Discussion on the temptation to incorrectly state the limit as X approaches 0.
Clarification that the limit does not exist at X equals 0 due to a jump discontinuity.
Task to find the limit as X approaches negative 0.7.
Observation of the flat line at X equals negative 0.7 leading to a Y value of negative 1.
Explanation of the concept of a continuous function and its relation to limits.
Emphasis on the absence of a limit when there is a jump discontinuity in a piecewise function.
Instruction that a limit can be found for a continuous function at a given point.
Illustration of how to approach limit problems with piecewise functions and discontinuities.
Summary of the importance of correctly identifying limits in piecewise functions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: