Introduction to torque | Moments, torque, and angular momentum | Physics | Khan Academy
TLDRThis presentation delves into the concept of torque, building upon the understanding of center of mass. It explains that applying force at the center of mass results in linear acceleration, while force applied elsewhere causes rotation. Torque, represented by the Greek letter tau (τ), is defined as the product of force and the perpendicular distance from the pivot point, measured in newton meters. The presentation clarifies that torque is not work, despite sharing units, and distinguishes between positive and negative torque based on the direction of rotation. It uses examples to illustrate calculations and the concept of mechanical advantage, emphasizing the importance of net torque in determining an object's rotational motion.
Takeaways
- 📚 Torque is a concept introduced in the context of the center of mass, where it was mentioned but not fully explained.
- 🔧 When force is applied at the center of mass, an object accelerates in the direction of the force.
- 🌀 If force is applied away from the center of mass, an object will rotate around the center of mass if it's free to do so.
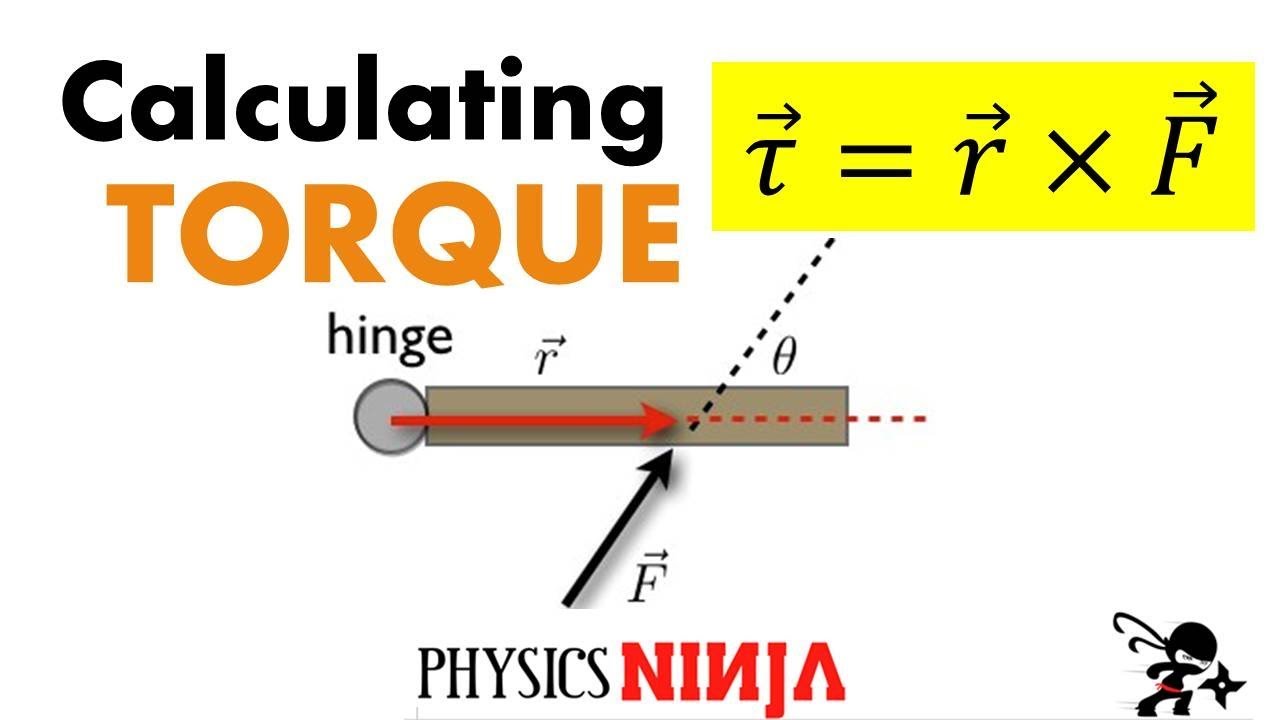
- 🔨 Torque (τ) is the force applied at a distance from the pivot point or center of mass, and it tends to cause rotation.
- 📏 Torque is calculated as the product of the force component perpendicular to the distance vector and the distance from the pivot point.
- 🔡 The Greek letter tau (τ) is used to represent torque.
- 🔢 Torque's unit is the newton meter (Nm), which is similar to the unit for work but the concepts are different.
- 🔄 The direction of rotation is significant: counterclockwise rotation results in positive torque, while clockwise rotation results in negative torque.
- 🔍 Torque can be visualized with the concept of a moment arm, which is the perpendicular distance from the axis of rotation to the point where force is applied.
- ⚖️ When an object is not rotating, the net torque acting on it is zero, allowing for calculations to balance forces and distances.
- 🤹♂️ Understanding torque is crucial for mechanical advantage concepts, which can be demonstrated by comparing the effects of forces applied at different distances from a pivot point.
Q & A
What is torque and how is it different from work?
-Torque is a measure of the force that can cause an object to rotate around an axis, and it is defined as force times the perpendicular distance from the axis of rotation. It is different from work, which involves the application of force over a distance in the same direction as the force, resulting in translation rather than rotation.
What is the Greek letter used to represent torque?
-The Greek letter used to represent torque is tau (τ), which looks like a curvy T.
What are the units of torque?
-The units of torque are newton meters (Nm), where force is measured in newtons and distance in meters.
How does the direction of rotation affect the sign of torque?
-In physics, if an object is rotating counterclockwise, the torque is considered positive. Conversely, if it is rotating clockwise, the torque is negative.
What is the term used for the perpendicular distance from the pivot point to the point where force is applied?
-The perpendicular distance from the pivot point to the point where force is applied is often called the moment arm distance.
Why is it important to understand the difference between torque and work?
-Understanding the difference between torque and work is important because they represent different physical phenomena: torque is related to rotational motion, while work is related to translational motion. This distinction is crucial for solving problems involving rotation and translation.
How can you determine if an object is not rotating?
-An object is not rotating if the net torque acting on it is zero. This means that the sum of all the torques acting on the object cancels out, resulting in no change in its rotational motion.
What is the relationship between torque and mechanical advantage?
-Torque is useful in understanding mechanical advantage because it allows you to calculate the forces and distances needed to achieve a desired rotation. If an object's rate of rotation is not changing, you can use the principle of zero net torque to solve for unknown forces or distances, which relates to the concept of mechanical advantage.
Can you provide an example of calculating torque from the script?
-Yes, in the script, an example is given where a force of 5 newtons is applied at a distance of 10 meters from the pivot point. The torque in this case is calculated as 5 newtons times 10 meters, which equals 50 newton meters.
What does it mean when the net torque on an object is zero?
-When the net torque on an object is zero, it means that the object is not rotating or its rate of rotation is not changing. This can occur when the torques acting on the object are balanced, such that they cancel each other out.
Why is it important to know the direction of the force relative to the distance vector when calculating torque?
-The direction of the force relative to the distance vector is important because torque is calculated using the component of the force that is perpendicular to the distance vector. If the force is not perpendicular, it will not contribute to the torque, and thus, will not cause rotation.
Outlines
🔧 Introduction to Torque and Its Basics
The first paragraph introduces the concept of torque, building upon the understanding of the center of mass from a previous presentation. It explains that applying force at the center of mass results in linear acceleration, whereas applying force away from the center causes rotation. The concept of torque is introduced as the rotational equivalent of force, with the Greek letter tau (τ) as its symbol. Torque is defined as the product of the force component perpendicular to the distance from the pivot point (or center of mass) and that distance itself, resulting in units of newton meters. The paragraph emphasizes the difference between torque and work, noting that while they share units, they represent fundamentally different physical phenomena: work involves the translation of an object, whereas torque is about rotation. The moment arm distance is highlighted as the perpendicular distance from the pivot point to the point of force application, and the term 'moment' is mentioned as an alternative name for torque in some contexts.
🔄 Calculating Torque and Understanding Its Direction
The second paragraph delves into the calculation of torque with a practical example involving a ruler as an object. It demonstrates that torque is calculated by multiplying the force applied to an object by the moment arm distance, which is the perpendicular distance from the pivot point to the line of action of the force. The paragraph clarifies the sign convention for torque: positive torque results in counterclockwise rotation, while negative torque corresponds to clockwise rotation. This is an important concept as it helps determine the direction of rotation induced by the applied force. The discussion also touches on the scenario where an object does not rotate, implying that the net torque acting on it is zero. By using this principle, one can solve for unknown forces or distances in a system where the net torque is known to be zero, as demonstrated with a mathematical example. The concept of mechanical advantage is briefly introduced, showing how forces applied at different distances can balance each other out, which is crucial for understanding the principles behind levers and other simple machines.
Mindmap
Keywords
💡Torque
💡Center of Mass
💡Force
💡Distance Vector
💡Pivot Point
💡Moment Arm
💡Rotation
💡Clockwise vs. Counterclockwise
💡Net Torque
💡Mechanical Advantage
💡Work
Highlights
Torque is introduced as a force that causes rotation around the center of mass or a pivot point.
Torque is represented by the Greek letter tau (τ).
Torque is calculated as the product of force and the perpendicular distance from the pivot point.
The unit of torque is the newton meter, similar to work but not the same.
Work involves force applied in the direction of movement, whereas torque involves a force perpendicular to the distance from the axis of rotation.
The moment arm distance is the perpendicular distance from the pivot point to where the force is applied.
Torque can be referred to as a moment in some physics contexts.
An example is given with a ruler and a pivot point to illustrate torque calculation.
Clockwise rotation results in negative torque, while counterclockwise gives positive torque.
The concept of net torque is introduced, which is the sum of all torques acting on an object.
If an object is not rotating, the net torque acting on it must be zero.
An example problem is solved to find the force needed to balance the torque from another force.
The concept of mechanical advantage is related to torque, where a smaller force applied at a greater distance can balance a larger force.
Torque is useful for understanding the conditions under which an object will or will not rotate.
The video concludes with an invitation to the next video for further exploration of torque.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: