Centripetal Force Physics Problems - Calculate Tension & Maximum Speed - Uniform Circular Motion
TLDRThis video script explores the concept of centripetal force, which is the force that keeps an object moving in a circular path. It explains how the direction of the force relative to an object's velocity affects its speed and direction. The script delves into examples of centripetal force in action, such as swinging a ball on a rope, the Earth's orbit around the Sun, a car turning, and a charge moving in a magnetic field. It also provides mathematical equations to calculate centripetal force and discusses how changes in mass, speed, and radius affect it. The video concludes with practical problems to apply the concepts learned, reinforcing the understanding of centripetal force and its calculations.
Takeaways
- 😀 If a force is parallel to the velocity vector of a moving ball, the ball will speed up.
- 😃 If the force is anti-parallel to the velocity vector, the ball will slow down.
- 😄 When the velocity vector is perpendicular to the force vector, the ball will turn at constant speed, changing direction.
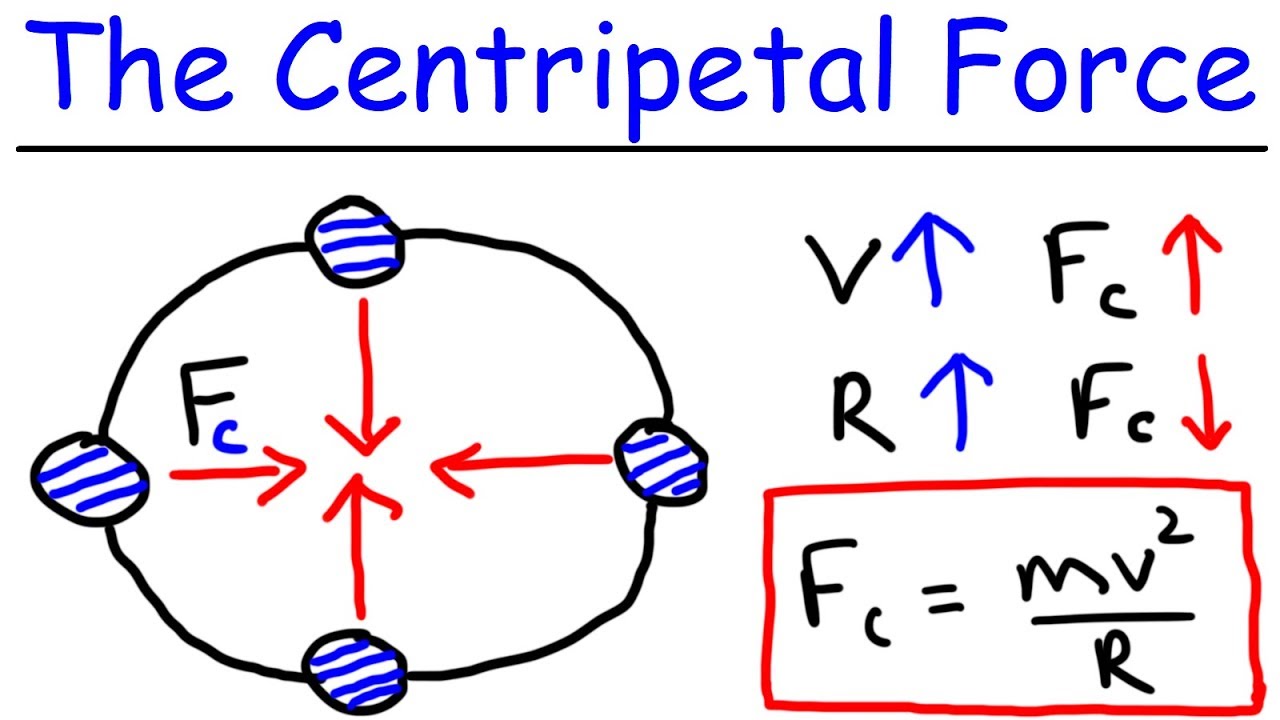
- 😁 The force that keeps an object moving in a circle is called centripetal force.
- 😆 Centripetal force is not a new kind of force but is provided by other forces such as tension, gravity, static friction, or magnetic force.
- 😅 In uniform circular motion, the centripetal force is always directed towards the center of the circle.
- 😂 Centripetal force (Fc) is calculated as Fc = mv^2/r, where m is mass, v is speed, and r is radius of the circle.
- 🤣 Doubling the mass or the speed increases the centripetal force, while increasing the radius decreases it.
- 😊 For a car making a turn, the tighter and faster the turn, the larger the centripetal force felt.
- 😇 Various examples of centripetal forces include tension in a rope for a spinning ball, gravity for planetary orbits, static friction for car turns, and magnetic force for moving charges in a magnetic field.
Q & A
What happens to a ball when the force acting on it is parallel to its velocity vector?
-When the force and velocity vectors are parallel, the ball will speed up because the force is adding energy in the direction of motion.
How does an anti-parallel force and velocity vector affect the speed of a ball?
-If the force and velocity vectors are anti-parallel, meaning they are opposite to each other, the ball will slow down as the force is acting against its motion.
What is the effect of a force that is perpendicular to the velocity vector on an object's motion?
-When the velocity vector is perpendicular to the force vector, the object will turn at a constant speed, changing its direction without changing the speed due to the centripetal force.
What is centripetal force and why is it not considered a new kind of force?
-Centripetal force is not a new kind of force; it's a term used to describe any force that causes an object to move in a circular path. It's provided by other forces such as tension, gravity, static friction, or magnetic force.
How does gravity provide the centripetal force for the Earth's orbit around the Sun?
-Gravity pulls the Earth towards the Sun, and because the Earth also has a tangential velocity, it falls towards the Sun while also moving forward, thus maintaining a curved, circular orbit.
What force provides the centripetal force when a car is turning?
-When a car is turning, the static frictional force between the tires and the road provides the centripetal force necessary for the car to follow a curved path.
How can the magnetic force act as a centripetal force?
-A magnetic force can act as a centripetal force when a moving charge (like a proton) is in a magnetic field. The magnetic force causes the charge to turn, effectively providing the inward force needed for circular motion.
What is the formula for calculating centripetal force according to Newton's second law?
-The formula for centripetal force is F_c = m * (v^2 / r), where F_c is the centripetal force, m is the mass of the object, v is its velocity, and r is the radius of the circular path.
How does the centripetal force change if the mass of an object is doubled?
-If the mass of an object is doubled, the centripetal force will also double, assuming all other factors like velocity and radius remain constant.
If the radius of the circular path is halved while the speed is doubled, what happens to the centripetal force?
-If the radius is halved and the speed is doubled, the centripetal force will increase by a factor of eight because the velocity term (v^2) increases by a factor of four and the radius term (1/r) doubles.
What is the relationship between the speed of an object in circular motion and the centripetal force required?
-The centripetal force required is directly proportional to the square of the speed of the object. If the speed increases, the centripetal force increases, and if the speed decreases, the centripetal force decreases.
How does the radius of the circular path affect the centripetal force?
-The centripetal force is inversely related to the radius of the circular path. If the radius increases, the centripetal force decreases, and if the radius decreases, the centripetal force increases.
What is the centripetal force acting on a 0.25 kg ball moving in a circle with a radius of 1.5 meters at 30 meters per second?
-The centripetal force acting on the ball can be calculated using the formula F_c = m * (v^2 / r). Substituting the given values, F_c = 0.25 kg * (30 m/s)^2 / 1.5 m = 150 N.
What is the radius of a circular turn made by a 500 kg car moving at 12 meters per second if the centripetal force is 9600 Newtons?
-Using the rearranged formula for radius r = (m * v^2) / F_c, and substituting the given values, r = (500 kg * (12 m/s)^2) / 9600 N = 7.5 meters.
What is the maximum speed a 0.35 kg ball can travel in a circle with a radius of 85 cm without breaking a rope that can withstand a maximum tension of 1500 Newtons?
-First, convert the radius to meters: 85 cm = 0.85 m. Then use the formula v = sqrt(F_c * r / m), where F_c is the tension force. Substituting the values, v = sqrt(1500 N * 0.85 m / 0.35 kg) ≈ 60.4 m/s.
Outlines
🚀 Introduction to Centripetal Force
The first paragraph introduces the concept of centripetal force, explaining its role in circular motion. It describes how a force parallel to the velocity vector accelerates an object, while an anti-parallel force decelerates it. When the force is perpendicular to the velocity, the object turns at a constant speed, exemplified by centripetal force. The paragraph also clarifies that centripetal force is not a distinct type of force but rather a term for any force that causes circular motion, such as tension in a rope swinging a ball, gravity in the Earth's orbit around the Sun, static friction in a car turn, and magnetic force on a moving charge in a magnetic field.
📚 Centripetal Force Equation and Its Implications
This paragraph delves into the mathematical representation of centripetal force, derived from Newton's second law as mass times centripetal acceleration. The centripetal acceleration formula is given as the square of velocity divided by the radius (v^2/r). The summary explains how centripetal force is directly proportional to mass and the square of velocity, and inversely proportional to the radius. It also discusses the effects of changing mass, speed, and radius on the centripetal force, using examples of driving a car and the physical sensations experienced during turns at different speeds and radii.
🔍 Calculation of Centripetal Force in Various Scenarios
The third paragraph presents practical examples to calculate centripetal force. It includes a ball moving in a horizontal circle, a car making a circular turn, and a ball attached to a rope. The examples are used to demonstrate how to apply the centripetal force formula in different contexts, such as calculating the force acting on an object or determining the maximum speed to prevent a rope from breaking. Each example is detailed step by step, providing the mathematical process and the final results.
📐 Free Body Diagrams and Tension Force Analysis
This paragraph discusses free body diagrams, particularly focusing on the tension force in a rope when an object is moving in a horizontal circle. It explains the components of the tension force (ftx and fty) and how they relate to the weight force (mg) of the object. The paragraph clarifies that at higher speeds, the tension force is approximately equal to the centripetal force (ftx), and provides an equation to calculate the exact tension force when the object is not moving horizontally. It also addresses the scenario where the tension force can be considered negligible compared to the centripetal force.
🌌 Asteroid Orbital Mechanics and Centripetal Force Variations
The fifth paragraph presents a hypothetical scenario involving three asteroids orbiting a moon, focusing on how changes in speed and radius affect the centripetal force. It explains how doubling the speed of an asteroid results in a quadrupled centripetal force. The summary also covers the case of an asteroid with a higher speed and a smaller radius, illustrating how the centripetal force increases significantly due to these changes. Formulas are provided to relate centripetal force to speed and radius, with a step-by-step guide to solving the given problems.
🚗 Real-World Application and Conceptual Understanding of Centripetal Force
The final paragraph ties the concept of centripetal force to real-world experiences, like driving a car and making turns. It emphasizes the importance of understanding how centripetal force is felt at different speeds and turn radii. The summary reinforces the idea that a wider turn at a slower speed results in a lower centripetal force, while a sharp turn at high speed results in a significant force. The paragraph concludes with a reminder of the importance of grasping the concept of centripetal force and its applications.
Mindmap
Keywords
💡Velocity Vector
💡Force
💡Centripetal Force
💡Uniform Circular Motion
💡Tension Force
💡Gravity
💡Static Friction
💡Magnetic Force
💡Newton's Second Law
💡Centripetal Acceleration
Highlights
If the force and velocity vectors are parallel, the ball is going to speed up.
If the force and velocity vectors are anti-parallel, the ball is going to slow down.
If the velocity vector is perpendicular to the force vector, the ball will turn at constant speed and change direction.
Centripetal force is not a new kind of force but is provided by another force, such as tension in a rope or gravity.
In a horizontal circle, the tension force in the rope provides the centripetal force.
Gravity provides the centripetal force that keeps the Earth in orbit around the Sun.
Static friction provides the centripetal force that allows a car to turn on the road.
The magnetic force can act as a centripetal force when a moving charge is in a magnetic field.
The centripetal force equation is F = mv^2/r, showing it's directly proportional to mass and the square of speed, and inversely proportional to the radius.
Increasing the mass or speed will increase the centripetal force, while increasing the radius will decrease it.
To reduce the feeling of centripetal force while turning, decrease speed and increase the turn radius.
If you double the mass, the centripetal force will also double; if you double the speed, the centripetal force will quadruple.
In practice problems, the centripetal force can be calculated using given mass, speed, and radius values.
If a rope can withstand a maximum tension force, the maximum speed of an object in a circular path can be determined without breaking the rope.
When an object moves fast enough in a horizontal circle, the tension force can be approximated as the centripetal force.
The exact tension force in a rope is the square root of the sum of the squares of the horizontal and vertical components of the tension force.
The centripetal force for asteroid Z, which orbits at half the radius but three times the speed of asteroid X, is 27,000 newtons.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: