Uniform Circular Motion and Centripetal Force
TLDRProfessor Dave's video script delves into the concept of uniform circular motion, a type of motion where objects follow a circular path. He explains that while linear motion has been extensively studied, circular motion requires a different set of equations to describe it accurately. The video uses the example of a Ferris wheel to illustrate how objects in circular motion, such as the wheel's cars, move at a constant radius around a central axis. The speed of these objects, known as tangential speed, is dependent on their distance from the axis of rotation. The script clarifies that uniform circular motion is characterized by a constant centripetal acceleration directed towards the center of the circular path. This acceleration results from a centripetal force, which is the force that keeps the object moving in a circle. The video also touches on the sensation of being pushed outwards on a rotating object, which is often mistakenly referred to as centrifugal force but is actually a result of inertia. The script concludes with a call to action for viewers to subscribe to the channel and support the content creator.
Takeaways
- 🌌 **Uniform Circular Motion**: Objects moving in a circular path follow a distinct set of equations that are essential for understanding the motion of planets and various earthbound objects like a Ferris wheel.
- 📏 **Tangential Speed**: The speed of an object in circular motion along the tangent to the circle at a given instant is known as tangential speed, which is influenced by the object's inertia to maintain a straight-line path.
- ⭕ **Constant Radius**: In uniform circular motion, the distance of the object from the axis of rotation remains constant, causing the object to trace a perfect circle.
- 🔄 **Angular Velocity**: Although not explicitly detailed in the script, it's implied that angular velocity is another key concept in circular motion, which will be discussed later.
- 🚀 **Centripetal Acceleration**: The constant change in the direction of the velocity vector in circular motion is due to centripetal acceleration, which always points towards the center of the circular path.
- ↗️ **Direction of Velocity**: At any moment in uniform circular motion, the velocity vector of an object is tangent to the circle, indicating the direction of motion.
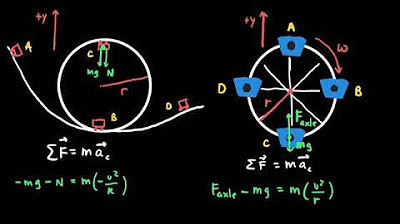
- 🔢 **Centripetal Acceleration Formula**: The centripetal acceleration is calculated as the square of the tangential speed divided by the radius of the path.
- 🤜 **Centripetal Force**: This force, directed towards the center of the circular path, is responsible for the circular motion and is calculated by multiplying the centripetal acceleration by the mass of the object.
- 🧲 **Centrifugal Force**: The sensation of being pushed outwards in a rotating frame, like a merry-go-round, is often referred to as centrifugal force, but it's not a real force; it's a result of inertia.
- 🪂 **Release and Tangent**: If the centripetal force is removed, an object in circular motion will continue along the tangent line at the point of release, following a straight-line path due to inertia.
- 🤝 **Friction and Circular Path**: On a rotating object, frictional force can cause an individual to follow a circular path if they hold on tightly, overcoming the inertia that would otherwise send them flying off.
Q & A
What is uniform circular motion?
-Uniform circular motion is a type of motion where an object moves in a circular path with a constant speed along the tangent line at any given point.
Why do we need to discuss tangential speed when describing the motion of a car on a Ferris wheel?
-Tangential speed is discussed because it is the speed of the car along the tangent line at a particular instant, which is the actual path the car is trying to follow due to its inertia to maintain a straight line motion.
How does the distance from the axis of rotation affect the tangential speed of an object in circular motion?
-The tangential speed is dependent on the distance from the axis of rotation; objects closer to the center of rotation have a shorter path to cover in a given time, resulting in a slower tangential speed compared to objects further from the center.
What is the relationship between centripetal acceleration and the radius of the circular path?
-Centripetal acceleration is given by the formula tangential speed squared over the radius of the path. This means that the acceleration increases if the object moves faster or is closer to the center of the circle.
Why is centripetal force necessary for an object to maintain circular motion?
-Centripetal force is necessary because it is the force that pulls an object towards the center of the circular path, which is required to change the direction of the velocity vector and maintain the circular motion.
What happens if the centripetal force is suddenly removed from an object in circular motion?
-If the centripetal force is removed, the object will no longer be pulled towards the axis of rotation and will instead move in a straight line tangent to the circle at the point of release.
What is the formula for calculating centripetal force?
-Centripetal force can be calculated using the formula F_c = m * a_c, where F_c is the centripetal force, m is the mass of the object, and a_c is the centripetal acceleration.
What is the role of inertia in the context of circular motion?
-Inertia is the property of an object to resist changes in its state of motion. In the context of circular motion, it causes the object to try to move in a straight line, which is why a centripetal force is needed to keep the object moving in a circle.
Why do we feel pushed outwards when on a rotating object like a merry-go-round?
-The feeling of being pushed outwards is due to the inertia of your body trying to maintain its straight-line motion. This is often referred to as centrifugal force, but it is not a real force; it is a result of the body's inertia.
What is the difference between centripetal and centrifugal force?
-Centripetal force is a real force that pulls an object towards the center of rotation, necessary for circular motion. Centrifugal force, on the other hand, is not a real force but rather a perceived effect due to the inertia of an object resisting changes to its straight-line motion.
What would happen if you let go of a ball on a string while spinning it in a circle?
-If you let go of the string, the centripetal force would be removed, and the ball would move in a straight line along the tangent to the circle at the point of release, due to the absence of a force to pull it towards the center.
How can we describe the force that must be applied to produce circular motion?
-The force required to produce circular motion can be described as the centripetal force, which is the force that acts towards the center of the circular path and is calculated as the mass of the object times the tangential speed squared over the radius of the path.
Outlines
🌌 Understanding Uniform Circular Motion
Professor Dave introduces the concept of uniform circular motion, contrasting it with linear motion and explaining its importance for understanding the motion of planets and various objects on Earth. He uses the example of a Ferris wheel to illustrate how objects exhibit circular motion around a central axis. The tangential speed, which is the speed along the tangent line at a given instant, is emphasized as a key factor in describing the motion. The professor also discusses the relationship between tangential speed, the radius of the wheel, and the angular velocity. He explains that uniform circular motion is maintained by a constant centripetal acceleration directed towards the center of the wheel, which is responsible for the continuous change in the direction of the velocity vector. The centripetal acceleration is calculated as the square of the tangential speed divided by the radius of the path. The centripetal force, which is the force that produces this acceleration, is described as the product of mass, acceleration, and is directed inward towards the axis of rotation. The professor also touches on the concept of centrifugal force, clarifying that it is not a real force but rather a sensation due to inertia, which is the tendency of an object to maintain its straight-line motion. He concludes with a safety note about the effects of inertia when riding a merry-go-round.
🚀 Centrifugal Force and Inertia in Circular Motion
In this paragraph, the script continues the discussion on circular motion, focusing on the effects of inertia and the concept of centrifugal force. It explains that if the centripetal force, which keeps an object in circular motion, is removed, the object would move in a straight line along the tangent at the point of release. The script uses the example of letting go of a string attached to a ball to illustrate this point. It also emphasizes that the sensation of being pushed outwards on a rotating object like a merry-go-round is due to inertia, not a real force. The script clarifies that inertia is a property related to Newton's first law, which states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external force. It concludes with a reminder that holding on tightly to a rotating object allows one to follow its circular path due to frictional force, and a cautionary note about the potential consequences of not doing so.
Mindmap
Keywords
💡Uniform Circular Motion
💡Tangential Speed
💡Centripetal Acceleration
💡Centripetal Force
💡Angular Velocity
💡Inertia
💡Frictional Force
💡Centrifugal Force
💡Newton's Second Law
💡Newton's First Law
💡Ferris Wheel
Highlights
Uniform circular motion involves objects following circular paths and is governed by a distinct set of equations.
Examples of uniform circular motion include the planets and various earthbound objects like a Ferris wheel.
In circular motion, objects move with a constant radius around a single axis of rotation.
Tangential speed is the speed of an object along the tangent line at a specific instant.
Uniform circular motion is characterized by a constant tangential speed.
The tangential speed of an object in circular motion depends on its distance from the axis of rotation.
Angular velocity is a concept that helps explain the counterintuitive nature of tangential speed in a rotating system.
Centripetal acceleration is constant and directed towards the center of the wheel, causing the circular motion.
The direction of the velocity vector in uniform circular motion is constantly changing due to centripetal acceleration.
Centripetal acceleration is calculated as the square of tangential speed divided by the radius of the path.
Newton's second law implies that a force is required to produce centripetal acceleration, known as the centripetal force.
Centripetal force is the force that maintains circular motion and can be due to tension, gravity, or friction.
If the centripetal force is removed, the object will move in a straight line along the tangent at the point of release.
Centrifugal force is not a real force but rather a sensation due to an object's inertia trying to maintain a straight path.
Inertia is a property derived from Newton's first law, not a force.
Frictional force can cause a person to follow a circular path on a rotating object like a merry-go-round.
If a person lets go on a rotating object, inertia will cause them to move off the object in a straight line.
The video provides a comprehensive understanding of uniform circular motion and its principles.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: