Lec 24 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThis educational video script from MIT OpenCourseWare covers fundamental concepts of physics, correcting a previous mistake by explaining that energy, heat, and work are interchangeable quantities with different units. It delves into probability theory using a dartboard example, illustrating how to calculate the likelihood of a person being hit by a dart. The script introduces mathematical models, such as the normal distribution function e^(-r^2), and explains the method of shells for calculating volumes of revolution. It also discusses numerical integration techniques, including Riemann sums, the trapezoidal rule, and Simpson's Rule, highlighting their efficiency and accuracy in approximating integrals without analytical solutions.
Takeaways
- 📚 The lecture begins with a correction on the terminology related to energy and heat, clarifying that in physics, they are the same concept and can be measured in various units.
- 🎯 The dartboard example is introduced to illustrate a probability problem, where the likelihood of a person being hit by a dart is calculated based on certain assumptions.
- 📉 The assumption made for the dartboard problem involves a normal distribution function, e^{-r^2}, which represents the number of hits being proportional to a constant times this function of the radius.
- 📐 The method of shells is used to calculate the volume of revolution, which represents the likelihood of hits in a certain section of the dartboard.
- ⚖️ The concept of 'part to whole' ratio is central to probability problems, where 'part' is the area of interest and 'whole' is the total possible outcomes.
- 🌟 The professor emphasizes that the constant of proportionality in the dart distribution is ambiguous and depends on the number of attempts made.
- 👦 The 'little brother' in the example is standing at a distance, and the probability of him being hit is calculated for a specific section of the dartboard.
- 📈 The probability of hitting the target (for a seven-year-old) is given as 1/2, and this information is used to calculate the probability of the little brother being hit.
- 📊 The lecture connects the dartboard example to concepts of weighted averages and integrals, highlighting the importance of the weight function in determining the distribution of hits.
- 📉 The second part of the lecture introduces numerical integration methods, starting with Riemann sums, which are noted to be inefficient.
- 📏 The trapezoidal rule is presented as an improvement over Riemann sums for approximating integrals, involving the calculation of trapezoids under the curve.
- 📘 Simpson's Rule is introduced as a more sophisticated method for numerical integration, which uses parabolic segments to approximate the area under a curve and is particularly effective for functions without inflection points.
Q & A
What was the mistake the professor corrected from the previous lecture?
-The professor corrected the mistake of referring to the computation in the candy bar example as energy instead of heat. He clarified that in physics, energy, heat, and work are all the same thing, just measured in different units.
What is the significance of the dartboard example in the lecture?
-The dartboard example is used to illustrate a probability problem where the likelihood of a person being hit by a dart is calculated based on certain assumptions about the distribution of hits on the dartboard.
What assumptions are made to model the dartboard hits distribution?
-The assumption made is that the number of hits is proportional to some constant times e^(-r^2), which represents a normal distribution as a function of the radius.
How does the professor describe the method of shells for calculating the volume of revolution in the dartboard example?
-The method of shells is used to calculate the volume of revolution by integrating between two radii, r_1 and r_2. The circumference of a small piece at a fixed distance r is 2 pi r, and the height is e^(-r^2), multiplied by the thickness dr.
What is the importance of the factor 'c' in the dartboard example?
-The factor 'c' represents the constant of proportionality in the distribution of hits. It is not explicitly known, but it cancels out when calculating the ratio of the part to the whole, making it irrelevant for the final probability calculation.
Why does the professor consider the whole to be from 0 to infinity when calculating the probability?
-The professor considers the whole to be from 0 to infinity because it simplifies the calculation. Although it is an idealization, the exponential decrease in the distribution means that the tail end contributions are negligible.
What is the probability calculation for the ring between radii r_1 and r_2 based on the model?
-The probability calculation for the ring between radii r_1 and r_2 is e^(-r_1^2) - e^(-r_2^2), which represents the ratio of the part (the ring) to the whole (all possible hit locations).
How does the professor justify the use of the function e^(-r^2) for modeling dart hits?
-The professor justifies the use of e^(-r^2) by referencing its historical use in modeling the distribution of V-2 rockets hitting London during World War II, indicating its accuracy and realism.
What is the significance of the little brother's location in the dartboard example?
-The little brother's location is significant because it defines the 'part' of the dartboard where the probability of him being hit is calculated. He is standing at a distance of approximately twice the radius of the target away.
How does the professor calculate the probability of the little brother being hit by a dart?
-The professor calculates the probability by determining the likelihood of a hit within a specific band of the dartboard (between 2a and 3a radius), and then scaling this probability by the chance of hitting the target itself, which is known to be 1/2.
What are the three numerical integration methods discussed in the script?
-The three numerical integration methods discussed are Riemann sums, the trapezoidal rule, and Simpson's Rule.
Why are numerical integration methods important?
-Numerical integration methods are important because many integrals do not have analytical solutions and must be computed using calculators or machines.
What is the basic idea behind Riemann sums?
-The basic idea behind Riemann sums is to approximate the integral of a function by summing the areas of rectangles or trapezoids under the curve of the function within a given interval.
How does the trapezoidal rule improve upon Riemann sums?
-The trapezoidal rule improves upon Riemann sums by using trapezoids instead of rectangles to approximate the area under the curve, which generally provides a better approximation.
What is Simpson's Rule and how does it work?
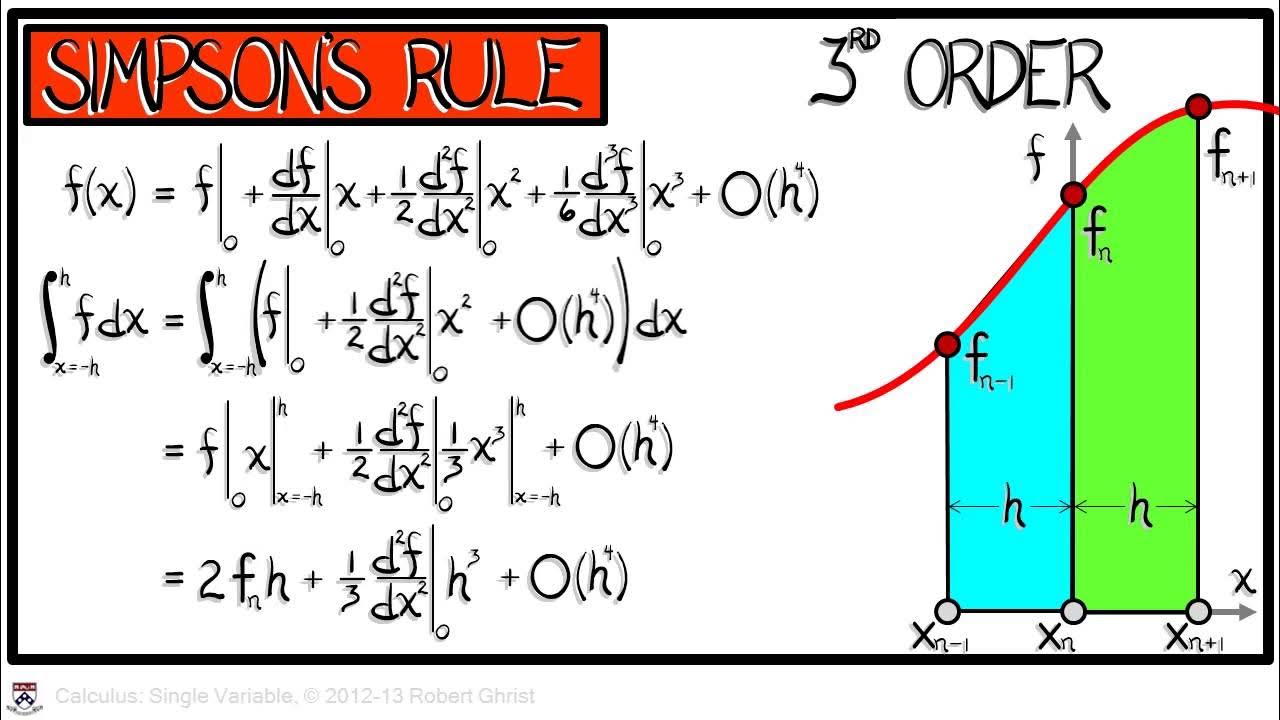
-Simpson's Rule is a numerical integration method that involves fitting a parabola to three points at a time and using the area under the parabola as the approximation for the integral. It emphasizes the middle point more than the ends, which often results in a more accurate approximation.
What is the formula for the average height in Simpson's Rule?
-The formula for the average height in Simpson's Rule is (y_0 + 4y_1 + y_2) / 6 for the first chunk, and it continues with a pattern of 1, 4, 1 for the weights of the function values at each interval.
Why is it required for n to be even in Simpson's Rule?
-In Simpson's Rule, n needs to be even because the method involves fitting parabolas between pairs of intervals, and an even n ensures that the function values at the endpoints can be paired appropriately.
How does the trapezoidal rule relate to the left and right Riemann sums?
-The trapezoidal rule is essentially the average of the left and right Riemann sums. It takes into account the function values at both the beginning and end of each interval, providing a more balanced approximation.
What is the main advantage of Simpson's Rule over the trapezoidal rule?
-The main advantage of Simpson's Rule over the trapezoidal rule is that it provides a more accurate approximation of the integral, especially for functions that do not have many inflection points and mostly wiggle in one direction.
Outlines
📚 Introduction to MIT OpenCourseWare and Physics Concepts
The professor begins by addressing a previous mistake regarding the terminology of energy and heat, clarifying that in physics, energy, heat, and work are essentially the same concept but measured in different units. The lecture then transitions into an example involving a dartboard to illustrate a probability problem. The scenario involves a target (dartboard), a person (little brother), and a dart thrower, aiming to calculate the likelihood of the person being hit by a dart. The professor introduces the concept of normal distribution, represented by the function e^(-r^2), to model the distribution of dart hits as a function of the radius from the center of the dartboard.
📐 Setting Up the Dartboard Probability Problem
The professor elaborates on the dartboard example by defining the 'part' and the 'whole' in the context of probability. The 'part' refers to the area where the little brother is standing, while the 'whole' encompasses all possible areas where a dart might land. The focus is on calculating the likelihood of darts hitting within specific concentric circles defined by radii r_1 and r_2. The method of shells is introduced to calculate the volume of revolution, which represents the likelihood of hits in a given section. The professor also explains why the height of the volume element is represented by the function e^(-r^2) and the circumference by 2 pi r, multiplied by the thickness dr.
🧩 Probability Distribution and Dartboard Hits
The discussion continues with the interpretation of the dartboard hits' probability distribution. The professor explains that the number of hits in a given area is proportional to the area itself and a constant of proportionality, which depends on the number of attempts made. The concept of the 'mode' is introduced, indicating the most likely spot to be hit (the center), but clarifies that the area around the center is small, making it less likely to be hit when considering the total volume. The professor also addresses the practicality of the chosen function e^(-r^2) by referencing its historical use in modeling the distribution of V-2 rocket hits during World War II.
🎯 Incorporating the Little Brother into the Dartboard Model
The professor introduces the 'little brother' into the dartboard model, explaining that the child is standing at a distance approximately twice the radius of the target, away from the dartboard. The brother's location is approximated by a sector of the dartboard's radius. The probability of the brother being hit by a dart is then related to the likelihood of the darts landing outside the target area. The professor emphasizes that the dart thrower often misses the target, which is a significant factor in the probability calculation.
📉 Calculating the Probability of Hitting the Target and the Brother
The professor provides a mathematical approach to calculating the probability of hitting the target and, by extension, the little brother. The 'part' of the probability is determined by integrating the function e^(-r^2) between the radii r_1 and r_2, resulting in the expression pi * (e^(-r_1^2) - e^(-r_2^2)). The 'whole' is considered to be the range from 0 to infinity, simplifying the calculation to c * pi * (1 - 0), where c is a constant that cancels out in the final probability ratio. The probability of landing on the target within a radius between r_1 and r_2 is thus the difference in the exponentiated terms, highlighting the idealization used in the model.
🔢 Probability Calculation and Numerical Integration Methods
The professor concludes the dartboard example by calculating the specific probability of the little brother being hit, given that the target's radius is 'a' and the brother stands between 2a and 3a from the center. The probability is derived to be approximately 1%, based on the model. The lecture then transitions into a new topic: numerical integration. The professor briefly introduces Riemann sums as a method for approximating integrals when analytical solutions are not available, setting the stage for a more in-depth discussion of numerical integration techniques in subsequent lectures.
📊 Exploring Numerical Integration: Riemann Sums and Beyond
The professor delves into the topic of numerical integration, starting with a review of Riemann sums, which involve dividing the integration interval into small segments and approximating the area under the curve by summing the products of function values and segment widths. The left and right Riemann sums are described, highlighting their limitations due to inefficiency. The professor then introduces the trapezoidal rule as an improvement over Riemann sums, which involves approximating the area under the curve with trapezoids instead of rectangles. The trapezoidal rule is presented as a more reasonable approach, though it is still not the most efficient method available.
📐 Simplifying the Trapezoidal Rule and Introducing Simpson's Rule
The professor simplifies the formula for the trapezoidal rule, which involves taking the average of the left and right Riemann sums, and presents it as a more efficient method than Riemann sums. However, it is noted that the trapezoidal rule is still not as accurate as desired. The lecture then introduces Simpson's Rule, a more advanced technique for numerical integration that involves fitting parabolas between intervals of the curve. Simpson's Rule is highlighted as a significant improvement over the trapezoidal rule, offering a better approximation for most functions without inflection points.
📘 Detailed Explanation of Simpson's Rule
The professor provides a detailed explanation of Simpson's Rule, which requires the number of intervals to be even and involves calculating the area under a parabola that fits through three points at a time. The formula for the average height under the parabola is given as a weighted average of the function values at those points: (y_0 + 4y_1 + y_2) / 6. The full formula for Simpson's Rule is presented, emphasizing the pattern of weights 1, 4, and 2 that alternates across the intervals. The rule is praised for its effectiveness in approximating integrals, especially when compared to the less efficient Riemann sums and the trapezoidal rule.
🔚 Conclusion and Preview of Upcoming Topics
The professor concludes the current lecture by summarizing the key points discussed, including the dartboard probability model and the introduction of numerical integration methods. A preview of the next lecture is given, where the professor promises to demonstrate the effectiveness of Simpson's Rule compared to other numerical integration techniques. The lecture ends with an open invitation for any remaining questions from the students.
Mindmap
Keywords
💡Creative Commons license
💡MIT OpenCourseWare
💡Energy, heat, and work
💡Probability
💡Normal distribution
💡Volume of revolution
💡Method of shells
💡Riemann sums
💡Trapezoidal rule
💡Simpson's Rule
💡Weighted averages
Highlights
Professor corrects a previous mistake regarding the terminology of energy and heat, emphasizing they are the same in physics.
Introduction of the dartboard example to illustrate a probability problem.
Assumption that the number of hits on a dartboard follows a normal distribution function e^(-r^2).
Explanation of the probability problem setup involving the ratio of the 'part' to the 'whole'.
Use of concentric circles to represent the 'part' and 'whole' in the dartboard probability example.
Introduction of the method of shells for calculating the volume of revolution in the dartboard example.
Discussion on why the likelihood of a hit is proportional to the area and the height represented by e^(-r^2).
Clarification on the arbitrary nature of constants in probability calculations and their eventual cancellation.
The concept of a mathematical model is introduced with the dartboard example, requiring justification.
Calculation of the probability of hitting a certain band on the dartboard using integration.
Explanation of the idealization in probability models, such as considering the dartboard hits ranging to infinity.
Derivation of the formula for the probability of landing on a target within a radius between r_1 and r_2.
Application of the dartboard model to estimate the probability of a younger brother getting hit.
Introduction and comparison of numerical integration methods: Riemann sums, the trapezoidal rule, and Simpson's Rule.
Detailed explanation of the trapezoidal rule as an improvement over Riemann sums for numerical integration.
Presentation of Simpson's Rule as an efficient method for numerical integration using parabolic approximation.
The formula for Simpson's Rule is explained, emphasizing its pattern of weights for an accurate integral approximation.
Transcripts
Browse More Related Video

Lec 25 | MIT 18.01 Single Variable Calculus, Fall 2007
Calculus Chapter 5 Lecture 49 Numerical Integration II

Numerical Integration With Trapezoidal and Simpson's Rule

Numerical Integration - Trapezoidal Rule & Simpson's Rule

Lec 23 | MIT 18.01 Single Variable Calculus, Fall 2007

Calculus AB Homework 6.2 Riemann and Trapezoidal Sums
5.0 / 5 (0 votes)
Thanks for rating: