Evaluating Trigonometric Functions Given a Point on the Terminal Side - Trigonometry

The Organic Chemistry Tutor
14 Oct 201710:48
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the fundamentals of trigonometry, focusing on the properties of right triangles and the unit circle. It explains the definitions of sine, cosine, tangent, cosecant, secant, and cotangent in relation to a triangle's sides and hypotenuse. The script also covers the signs of these functions in different quadrants, using mnemonic devices like 'all students take calculus' to aid memorization. Practical examples demonstrate how to calculate these trigonometric functions given a point's coordinates, with step-by-step instructions for plotting points and applying the Pythagorean theorem to find the hypotenuse when necessary.

Takeaways
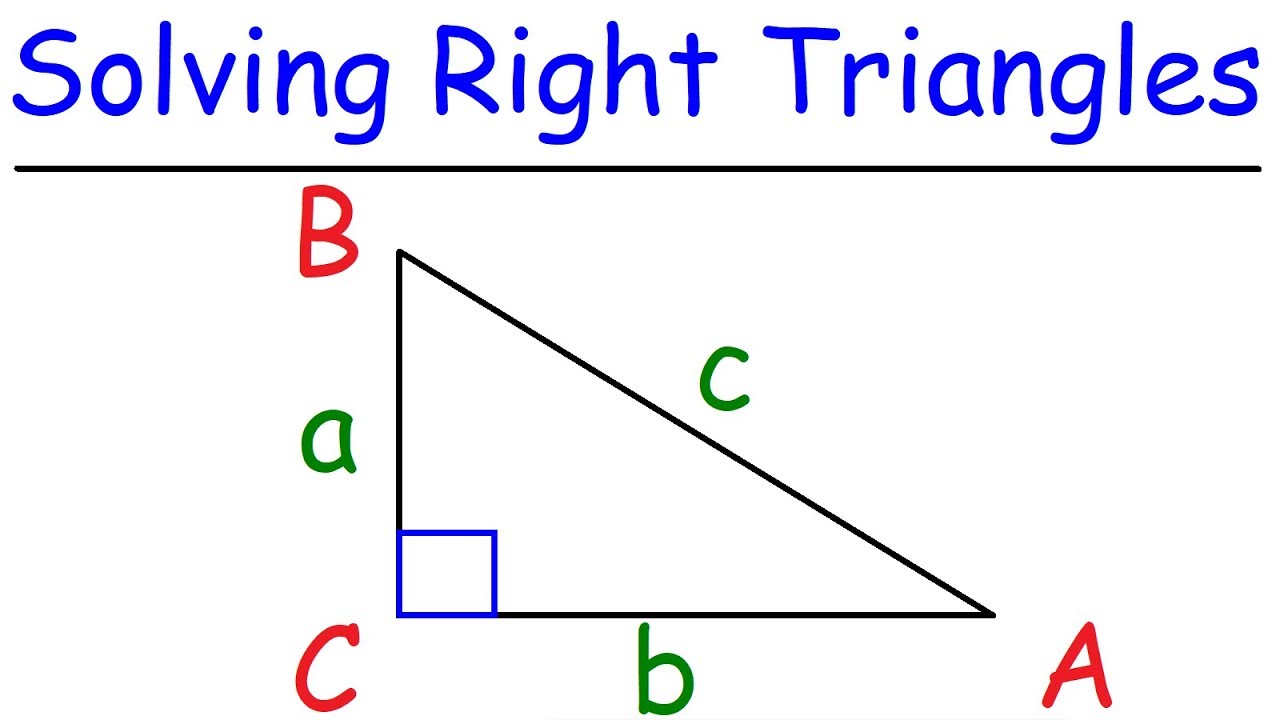
  • 📐 The hypotenuse of a right triangle is denoted as 'r', and the sides adjacent to angle theta are 'x' and 'y'.
  • 🧭 In a unit circle, 'r' is equal to 1, simplifying the sine equation to sine theta equals 'y'.
  • 📉 The sine of an angle is the ratio of the opposite side to the hypotenuse, and cosine is the ratio of the adjacent side to the hypotenuse.
  • 🔄 Tangent is the ratio of the opposite side to the adjacent side, and its reciprocal functions are cosecant, secant, and cotangent.
  • 📈 The signs of trigonometric functions vary across the four quadrants of the unit circle, with 'sine' positive in quadrants I and II, 'cosine' positive in quadrants I and IV, and 'tangent' positive in quadrants I and III.
  • 📚 Mnemonics like 'all students take calculus' can help remember the signs of sine, cosine, and tangent in quadrant I.
  • 📍 To find the trigonometric functions for a given point, plot the point and construct a right triangle using the coordinates and hypotenuse.
  • 📊 For a point like (-5, 12), calculate the trigonometric functions using the coordinates as the sides of the triangle and the Pythagorean theorem to find the hypotenuse.
  • 📈 The values of sine, cosine, and tangent can be used to find their reciprocal functions: cosecant, secant, and cotangent.
  • 🤔 The example of point (-8, -15) illustrates how to determine trigonometric function values in quadrant III, where sine and cosine are negative, but tangent is positive.
  • 🔢 For a non-special triangle like (2, -4), use the Pythagorean theorem to find the hypotenuse and then calculate the trigonometric functions accordingly.
Q & A

  • What is the hypotenuse of a right triangle in the context of trigonometry?

    -In the context of trigonometry, the hypotenuse of a right triangle is the longest side, which is opposite the right angle. It is typically denoted by 'r' in the script.

  • What does sine theta represent in a right triangle?

    -Sine theta (sin(θ)) represents the ratio of the length of the side opposite the angle theta to the length of the hypotenuse. In a unit circle, where the hypotenuse is 1, sin(θ) = y/1 = y.

  • According to the script, what is the relationship between cosine theta and the sides of a right triangle?

    -Cosine theta (cos(θ)) is equal to the length of the adjacent side to the angle theta divided by the length of the hypotenuse (r). So, cos(θ) = x/r.

  • How is tangent theta defined in terms of the sides of a right triangle?

    -Tangent theta (tan(θ)) is defined as the ratio of the length of the side opposite the angle theta to the length of the adjacent side. It can be expressed as tan(θ) = y/x.

  • What are the reciprocal trigonometric functions of sine and cosine?

    -The reciprocal trigonometric functions of sine and cosine are cosecant and secant, respectively. Cosecant (csc(θ)) is the reciprocal of sine, so csc(θ) = r/y, and secant (sec(θ)) is the reciprocal of cosine, so sec(θ) = r/x.

  • What is the cotangent function in trigonometry?

    -Cotangent (cot(θ)) is the reciprocal of the tangent function. It is defined as the ratio of the length of the adjacent side to the length of the opposite side, or cot(θ) = x/y.

  • How do the signs of trigonometric functions vary across different quadrants?

    -The signs of trigonometric functions vary as follows: sine is positive in quadrants I and II, negative in quadrants III and IV; cosine is positive in quadrants I and IV, negative in quadrants II and III; tangent is positive in quadrants I and III, negative in quadrants II and IV.

  • What is the mnemonic 'all students take calculus' referring to in the context of trigonometry?

    -The mnemonic 'all students take calculus' is a way to remember the signs of trigonometric functions in the different quadrants. 'A' stands for 'all' which corresponds to quadrant I where all functions are positive; 'S' stands for 'students' which corresponds to quadrant II where sine is positive; 'T' stands for 'take' which corresponds to quadrant III where tangent is positive; 'C' stands for 'calculus' which corresponds to quadrant IV where cosine is positive.

  • If a point P is given as (-5, 12) and lies on the terminal side of theta, how can you find the trigonometric functions of theta?

    -To find the trigonometric functions of theta given point P (-5, 12), you plot the point, draw a right triangle with the x-axis, and calculate the hypotenuse 'r'. Then, use the coordinates and hypotenuse to find sine, cosine, and tangent of theta. The other three functions (cosecant, secant, and cotangent) are found by taking the reciprocals of sine, cosine, and tangent, respectively.

  • How is the hypotenuse 'r' of a right triangle calculated if it's not a special triangle?

    -If the triangle is not a special triangle (like 3-4-5, 5-12-13, etc.), you calculate the hypotenuse 'r' using the Pythagorean theorem: r = √(x² + y²), where 'x' and 'y' are the lengths of the other two sides.

  • Given the point (2, -4), how would you find the value of sine theta?

    -For the point (2, -4), you first calculate the hypotenuse 'r' using the Pythagorean theorem. Then, sine theta (sin(θ)) is found by dividing the y-coordinate (opposite side) by the hypotenuse 'r'. After finding sine theta, you can rationalize the denominator if necessary.

  • Can you provide an example of how to find the value of tangent theta for the point (-8, -15)?

    -For the point (-8, -15), you first identify that it lies in quadrant III. Then, calculate sine and cosine using the coordinates and the hypotenuse. Since tangent is the ratio of sine to cosine (tan(θ) = sin(θ)/cos(θ)), and both sine and cosine are negative in quadrant III, their division results in a positive value for tangent theta.

Outlines
00:00
📐 Introduction to Trigonometric Functions

This paragraph introduces the basic concepts of trigonometry, focusing on the relationships within a right triangle. It explains sine, cosine, and tangent in terms of their definitions using the sides of the triangle. The importance of these functions in the context of the unit circle, where the hypotenuse (r) is equal to one, is emphasized. The paragraph also covers the reciprocal trigonometric functions: cosecant, secant, and cotangent.

05:02
🧮 Quadrants and Trigonometric Function Signs

This section reviews the signs of trigonometric functions in different quadrants of the coordinate plane. It explains that sine is positive in quadrants I and II, cosine is positive in quadrants I and IV, and tangent is positive in quadrants I and III. The mnemonic 'All Students Take Calculus' is introduced to help remember which functions are positive in each quadrant: all functions in quadrant I, sine in quadrant II, tangent in quadrant III, and cosine in quadrant IV.

10:04
🔢 Example Problem: Finding Trigonometric Functions

Using the point (-5, 12), this paragraph demonstrates how to find the six trigonometric functions. The process involves plotting the point, creating a right triangle, and calculating the hypotenuse using the Pythagorean theorem. The values for sine, cosine, and tangent are found, followed by their reciprocals: cosecant, secant, and cotangent. The example shows how to handle negative values and use reference angles.

📊 Second Example: Negative Coordinates

The second example uses the point (-8, -15) to find trigonometric functions. After plotting the point in quadrant III, the hypotenuse is calculated, and sine, cosine, and tangent are determined, considering the signs in this quadrant. The reciprocals are also found, emphasizing that tangent is positive while sine and cosine are negative in quadrant III.

📏 Final Example: Using the Pythagorean Theorem

The final example involves the point (2, -4) and requires the Pythagorean theorem to find the hypotenuse. The values for sine, cosine, and tangent are calculated, with an emphasis on rationalizing denominators for sine and cosine. The reciprocals are also derived, demonstrating how to handle square roots in the denominators. This example reinforces the process for finding trigonometric functions from a given point.

Mindmap
Keywords
💡Right Triangle
A right triangle is a type of triangle that has one angle measuring exactly 90 degrees. In the context of the video, the right triangle is used to define trigonometric functions such as sine, cosine, and tangent through the relationship of its sides to the hypotenuse. For example, the script describes a right triangle with sides x and y and hypotenuse r, where angle theta is used to express these trigonometric ratios.
💡Hypotenuse
The hypotenuse is the longest side of a right triangle, and it is always opposite the right angle. In the video, the hypotenuse is denoted by 'r' and is fundamental in calculating trigonometric functions, as seen when defining sine and cosine in terms of the opposite side divided by the hypotenuse.
💡Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. The video focuses on six trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. These functions are central to the script's theme of explaining how to find the values of these functions given a point on the terminal side of an angle.
💡Sine (sin)
Sine is one of the primary trigonometric functions, defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse in a right triangle. In the script, sine theta (sin θ) is calculated as y/r, and it is used to find the sine value for different points on the terminal side of an angle.
💡Cosine (cos)
Cosine is another fundamental trigonometric function, which is the ratio of the length of the adjacent side to the hypotenuse in a right triangle. The script uses cosine theta (cos θ) to illustrate how to find the cosine value, defined as x/r, for a given point.
💡Tangent (tan)
Tangent is a trigonometric function that measures the ratio of the opposite side to the adjacent side in a right triangle. It is also expressed as the ratio of sine to cosine. In the script, tangent theta (tan θ) is calculated as y/x, and it is used to determine the tangent value for various points.
💡Cosecant (csc)
Cosecant is the reciprocal of the sine function, meaning it is the ratio of the hypotenuse to the opposite side. The script explains that if sine is y/r, then cosecant is r/y, and it is used to find the cosecant value when given a point on the terminal side of an angle.
💡Secant (sec)
Secant is the reciprocal of the cosine function, which is the ratio of the hypotenuse to the adjacent side. The video script mentions that if cosine is x/r, then secant is r/x, and it is used to find the secant value for a given point.
💡Cotangent (cot)
Cotangent is the reciprocal of the tangent function, and it is the ratio of the adjacent side to the opposite side in a right triangle. The script explains that cotangent is x/y, and it is used to find the cotangent value for different points on the terminal side of an angle.
💡Unit Circle
The unit circle is a circle with a radius of one and is centered at the origin of a coordinate system. It is used to define trigonometric functions for all angles. The script mentions that when dealing with the unit circle, the hypotenuse 'r' is one, which simplifies the sine function to sine theta being equal to the y-value.
💡Quadrants
Quadrants refer to the four equal areas created by the intersection of the x and y axes on a Cartesian coordinate system. The script discusses the signs of trigonometric functions in each quadrant, which is crucial for determining the values of sine, cosine, and tangent in different regions of the coordinate plane.
💡Pythagorean Theorem
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b), or a^2 + b^2 = c^2. In the script, the theorem is used to calculate the hypotenuse 'r' when the lengths of the other two sides are known, which is essential for finding trigonometric function values.
Highlights

Introduction to converting a triangle into a right triangle with hypotenuse 'r', sides 'x' and 'y', and angle 'theta'.

Explanation of sine theta as the ratio of the opposite side to the hypotenuse.

Clarification that in a unit circle, 'r' is one, simplifying sine theta to 'y'.

Definition of cosine theta as the ratio of the adjacent side to the hypotenuse according to SOHCAHTOA.

Description of tangent theta as the ratio of the opposite side to the adjacent side.

Introduction to reciprocal trigonometric functions: cosecant, secant, and cotangent.

Mnemonic for trigonometric function signs in different quadrants: 'All Students Take Calculus'.

Method to find the six trigonometric functions given a point on the terminal side of theta.

Example problem using point (-5, 12) to find trigonometric function values.

Step-by-step calculation of sine, cosine, and tangent for the point (-5, 12).

Calculation of reciprocal trigonometric functions for the point (-5, 12).

Second example problem using point (-8, -15) to find trigonometric function values.

Explanation of how to plot the point (-8, -15) and determine the triangle's quadrant.

Calculation of sine, cosine, and tangent for the point (-8, -15) in Quadrant III.

Determination of reciprocal trigonometric functions for the point (-8, -15).

Third example problem with point (2, -4) and the use of the Pythagorean theorem.

Detailed calculation of sine, cosine, and tangent for the point (2, -4).

Final calculation of reciprocal trigonometric functions for the point (2, -4).

Transcripts

Browse More Related Video

Trig - 0.6 Trig Functions of Acute Angles

Trig - 0.7 Trig Functions of Any Angle

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Basic Trigonometry: Sin Cos Tan (NancyPi)

Trigonometry - How To Solve Right Triangles

Trigonometry

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Trigonometry BasicsRight TrianglesUnit CircleSOHCAHTOATrigonometric FunctionsSine Cosine TangentQuadrant SignsMnemonicsTrigonometry ExamplesMath Education