How To Balance Nuclear Equations In Chemistry

The Organic Chemistry Tutor
19 Jun 202010:46
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script offers a step-by-step guide on balancing nuclear equations. It explains the process of identifying missing elements in nuclear reactions, such as beta decay and alpha decay, by ensuring mass and atomic number conservation. The script uses examples like carbon-14 decaying into nitrogen, nitrogen-14 bombarded with neutrons, thorium-230 undergoing alpha decay, mercury-201 capturing an electron, and uranium-238 reacting with carbon atoms. Each example demonstrates how to calculate the mass number and atomic number of the missing element and then identify it using the periodic table. The video aims to teach viewers the fundamental principles of nuclear reactions and the importance of balancing equations in nuclear physics.

Takeaways
  • 🔬 Balancing Nuclear Equations: The video explains the process of balancing nuclear equations by ensuring that the mass number and atomic number are conserved on both sides of the equation.
  • 🚫 Beta Decay: Carbon-14 undergoes beta decay, which involves the emission of a beta particle (electron), and the video demonstrates how to find the missing element in this reaction.
  • 🔢 Mass Number Conservation: The importance of keeping the mass number the same on both sides of the equation is highlighted, with examples showing how to calculate the mass number of the missing element.
  • ⚛️ Atomic Number Conservation: The video emphasizes the need to maintain the atomic number (nuclear charge) balance, which helps in identifying the missing element.
  • 🧪 Periodic Table Utilization: The script illustrates how to use the periodic table to determine the missing element based on its atomic number.
  • 🌐 Neutron Bombardment: An example of nitrogen-14 being bombarded by neutrons in the upper atmosphere to produce hydrogen and a missing element is provided, showing how to balance the equation.
  • 💥 Alpha Decay: The concept of alpha decay is introduced with thorium-230 as an example, where the missing element is identified by calculating the mass and atomic numbers.
  • 💫 Electron Capture: Mercury-201 undergoing electron capture to produce a gamma particle and a missing element is discussed, with the process of identifying the element explained.
  • 🎯 Isotope Transformation: The video shows how isotopes can transform into different elements through nuclear reactions, such as mercury-201 turning into gold-201.
  • 🌟 Nuclear Reaction Examples: Multiple examples of nuclear reactions, including those involving alpha particles, neutrons, and electron capture, are provided to demonstrate the balancing process.
  • 📚 Educational Content: The script serves as an educational resource, teaching viewers how to balance nuclear equations step by step with clear examples.
Q & A

  • What is the significance of balancing nuclear equations?

    -Balancing nuclear equations is crucial to ensure that the mass and the total nuclear charge are conserved in a nuclear reaction, as per the principles of conservation of mass and charge.

  • What does the atomic number represent in the context of nuclear equations?

    -The atomic number represents the number of protons in the nucleus of an atom, which is also equal to the nuclear charge and helps identify the element.

  • What is the mass number and how is it related to the number of protons and neutrons?

    -The mass number is the sum of the number of protons and neutrons in an atomic nucleus. It is used to distinguish isotopes of an element.

  • What is beta decay and how does it affect the atomic number and mass number of an element?

    -Beta decay is a type of radioactive decay where an electron (beta particle) is emitted from an atomic nucleus. This process increases the atomic number by one while decreasing the mass number by one, transforming the element into another.

  • What is the role of the periodic table in identifying the missing element in a nuclear equation?

    -The periodic table is used to identify the missing element in a nuclear equation by matching the calculated atomic number to the corresponding element.

  • What is the missing element when Carbon-14 undergoes beta decay?

    -When Carbon-14 undergoes beta decay, it transforms into Nitrogen, as the atomic number increases by one (from 6 to 7) while the mass number remains the same (14).

  • How can you determine the mass number of the missing element in a nuclear reaction?

    -The mass number of the missing element can be determined by ensuring the mass number is conserved in the reaction. By balancing the mass numbers on both sides of the equation, you can calculate the mass number of the missing element.

  • What is alpha decay and what particles are emitted during this process?

    -Alpha decay is a type of radioactive decay where an alpha particle, which is essentially a helium nucleus consisting of two protons and two neutrons, is emitted from the nucleus.

  • What element is produced when Thorium-230 undergoes alpha decay?

    -When Thorium-230 undergoes alpha decay, it produces Radium-226, as the mass number decreases by 4 and the atomic number decreases by 2.

  • What is electron capture and how does it affect the atomic number of an element?

    -Electron capture is a process where a proton-rich nucleus captures an electron from an inner electron shell, converting a proton into a neutron and thereby decreasing the atomic number by one.

  • What element is formed when Mercury-201 undergoes electron capture?

    -When Mercury-201 undergoes electron capture, it transforms into Gold-201, as the atomic number decreases by one (from 80 to 79) while the mass number remains unchanged.

  • How can you identify the missing element when Aluminum-27 is bombarded with an alpha particle?

    -By balancing the nuclear equation, you can determine that the missing element has a mass number of 30 and an atomic number of 15, which corresponds to Phosphorus.

  • What element is produced when Uranium-238 is bombarded with carbon atoms, generating six neutron particles?

    -When Uranium-238 is bombarded with carbon atoms and generates six neutron particles, the missing element produced is Californium-244, with a mass number of 244 and an atomic number of 98.

Outlines
00:00
🔬 Balancing Nuclear Equations with Carbon-14 Beta Decay

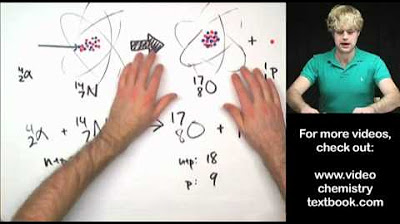
This paragraph introduces the process of balancing nuclear equations, using carbon-14 as an example undergoing beta decay. Beta decay involves the emission of an electron, transforming the element. To balance the equation, the atomic number and mass number must be conserved. Carbon-14 has 6 protons and 8 neutrons, making a total mass number of 14. The nuclear charge (atomic number) is 6. After beta decay, the missing element on the product side must have an atomic number that sums up to 6 on the right side of the equation and a mass number that balances the 14 on both sides. By solving the equation, it's determined that the missing atomic number is 7, which corresponds to nitrogen on the periodic table. The balanced equation shows mass and nuclear charge conservation.

05:01
🌟 Nuclear Reactions of Nitrogen-14, Thorium-230, Mercury-201, and Aluminum-27

This paragraph presents a series of nuclear reaction examples to practice balancing equations. Nitrogen-14 is bombarded by neutrons, resulting in the production of hydrogen and the regeneration of carbon-14. Thorium-230 undergoes alpha decay, emitting a helium nucleus, and the missing element is radium with mass 226 and atomic number 88. Mercury-201 experiences electron capture, turning into gold-201 with a mass of 201 and atomic number 79. Aluminum-27, when bombarded with an alpha particle, produces a neutron and phosphorus with mass 30 and atomic number 15. Each reaction is explained step by step, emphasizing the conservation of mass number and atomic number to identify the products and balance the equations.

10:01
💥 Uranium-238 Bombardment and the Formation of Californium-244

The final paragraph discusses a nuclear reaction where uranium-238 is bombarded with carbon atoms, resulting in the generation of six neutron particles and an unknown element. The mass number of the missing element is calculated to be 244 by adding the mass numbers of uranium-238 and carbon (12) and then subtracting the mass of the six neutrons (6). The atomic number is determined by adding the atomic numbers of uranium (92) and carbon (6), resulting in 98. The element with an atomic number of 98 is identified as californium. This example concludes the video with a clear demonstration of balancing a complex nuclear equation.

Mindmap
Keywords
💡Nuclear Equations
Nuclear equations are mathematical expressions that describe nuclear reactions, including decay processes and particle interactions. They are essential for understanding the changes in atomic structure during these reactions. In the video, balancing nuclear equations is the central theme, as the script walks through the process of ensuring mass and atomic number conservation in various nuclear reactions.
💡Carbon-14
Carbon-14 is a radioactive isotope of carbon with 6 protons and 8 neutrons, giving it a mass number of 14. It is used as a dating tool in archaeology and other scientific fields due to its predictable decay rate. In the video script, Carbon-14 is presented as an example of an isotope undergoing beta decay, emitting an electron and transforming into another element.
💡Beta Decay
Beta decay is a type of radioactive decay in which a beta particle (an electron or positron) is emitted from an atomic nucleus. This process changes the atomic number of the nucleus, transmuting one element into another. The script explains beta decay in the context of Carbon-14 emitting an electron and becoming another element, nitrogen in this case.
💡Atomic Number
The atomic number of an element is a fundamental property that represents the number of protons in the nucleus of an atom. It is what defines the element and its position on the periodic table. The video script emphasizes the importance of the atomic number in identifying the missing element in a nuclear reaction, as seen when determining nitrogen as the product of Carbon-14 beta decay.
💡Mass Number
The mass number of an isotope is the sum of the number of protons and neutrons in an atomic nucleus. It is a key piece of information used in nuclear equations to ensure that mass is conserved during nuclear reactions. The script illustrates this by showing how to balance the mass number on both sides of the equation, as in the example of nitrogen-14 being bombarded with neutrons.
💡Neutron Bombardment
Neutron bombardment refers to the process where an atomic nucleus is struck by neutrons, often leading to nuclear reactions such as the formation of new isotopes or elements. In the script, nitrogen-14 is bombarded with neutrons in the upper atmosphere, resulting in the production of hydrogen and the regeneration of carbon-14.
💡Alpha Decay
Alpha decay is a radioactive process in which an atomic nucleus emits an alpha particle, which is equivalent to a helium-4 nucleus consisting of two protons and two neutrons. This decay reduces the mass number by four and the atomic number by two. The script uses thorium-230 as an example, which undergoes alpha decay to form radium-226.
💡Electron Capture
Electron capture is a process where a proton-rich nucleus captures an electron from an inner electron shell, converting a proton into a neutron and emitting a neutrino. This decreases the atomic number by one while the mass number remains unchanged. In the video, mercury-201 undergoes electron capture, transforming into gold-201.
💡Isotopes
Isotopes are variants of a chemical element that have the same number of protons but different numbers of neutrons. This results in the same atomic number but different mass numbers. The script discusses several isotopes, such as carbon-14 and mercury-201, and how they undergo nuclear reactions to form new elements or isotopes.
💡Periodic Table
The periodic table is a tabular arrangement of the chemical elements, ordered by their atomic number, electron configuration, and recurring chemical properties. It is used to identify elements based on their atomic number. The video script mentions using the periodic table to determine the missing element in a nuclear reaction, such as identifying nitrogen after Carbon-14's beta decay.
Highlights

Introduction to balancing nuclear equations.

Carbon 14 undergoes beta decay, emitting a beta particle or electron.

Balancing a nuclear equation requires equal mass and total nuclear charge on both sides.

Identifying the missing element by balancing the atomic number and mass number.

Using algebra to solve for the missing atomic number in a nuclear equation.

Nitrogen identified as the missing element in the carbon 14 beta decay example.

Nitrogen 14 bombarded with neutrons produces hydrogen and a missing element.

Writing equations to determine the mass number and atomic number of missing elements.

Carbon identified as the missing element in the nitrogen 14 neutron bombardment example.

Thorium 230 undergoes alpha decay, and the missing element is to be identified.

Calculating the mass and atomic number of the missing element after thorium 230 alpha decay.

Radium identified as the missing element in the thorium 230 alpha decay example.

Mercury 201 undergoes electron capture, producing a gamma particle and a missing element.

Identifying gold as the missing element after mercury 201 electron capture.

Aluminum 27 bombarded with an alpha particle produces a neutron and a missing element.

Phosphorus identified as the missing element in the aluminum 27 alpha particle bombardment example.

Uranium 238 bombarded with carbon atoms generates six neutrons and a missing element.

Calculating the mass number and atomic number for the missing element in uranium 238 bombardment.

Californium identified as the missing element in the uranium 238 carbon bombardment example.

Conclusion of the video on how to balance nuclear equations.

Transcripts

Browse More Related Video

Conservation of Charge in Reactions

Alpha Decay

Alpha Decay, Beta Decay, Gamma Decay - Electron Capture, Positron Production - Nuclear Chemistry

Alpha Particles, Beta Particles, Gamma Rays, Positrons, Electrons, Protons, and Neutrons

Conservation of Nucleon Number

Nuclear Transmutation Part 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Nuclear EquationsEducationalPhysicsBeta DecayCarbon-14Nitrogen-14Thorium-230Mercury-201Electron CaptureAluminum-27Uranium-238