Critical Points, Increasing and Decreasing, Local Extrema Example with Rational Function
TLDRThis educational video script focuses on identifying critical points of a function to determine intervals of increase and decrease, as well as local extrema. It emphasizes the importance of considering the domain of the function, especially where the denominator is zero, which leads to domain restrictions at x = ±1. The script discusses finding horizontal and vertical asymptotes, intercepts, and critical points by analyzing the first derivative using the quotient rule. It also highlights the subtlety between points where the derivative does not exist and actual critical points. A sign chart is used to determine the function's behavior, concluding with a local maximum at x = 0. The script serves as a comprehensive guide to understanding function analysis, including the significance of writing out final answers.
Takeaways
- 📚 The video discusses finding critical points, intervals of increase/decrease, and local extrema of a function.
- 🚫 It emphasizes the importance of considering the domain of the function, especially where the denominator is zero (x = ±1), which are excluded from the domain.
- 📉 The function has vertical asymptotes at x = 1 and x = -1, and a horizontal asymptote at y = 1, which are determined by analyzing the function's behavior as x approaches infinity or the points where the function is undefined.
- 🔍 The y-intercept is found by setting x = 0, resulting in the point (0,0), and the x-intercept is also at the origin, as setting the function equal to zero yields x = 0.
- 📝 The first derivative of the function is calculated using the quotient rule, which is crucial for finding critical points.
- ❗ The derivative does not exist at x = ±1, but these are not considered critical points since the original function is undefined at these points.
- 🔍 To find critical points, set the first derivative equal to zero, which in this case yields x = 0, a valid critical point within the domain.
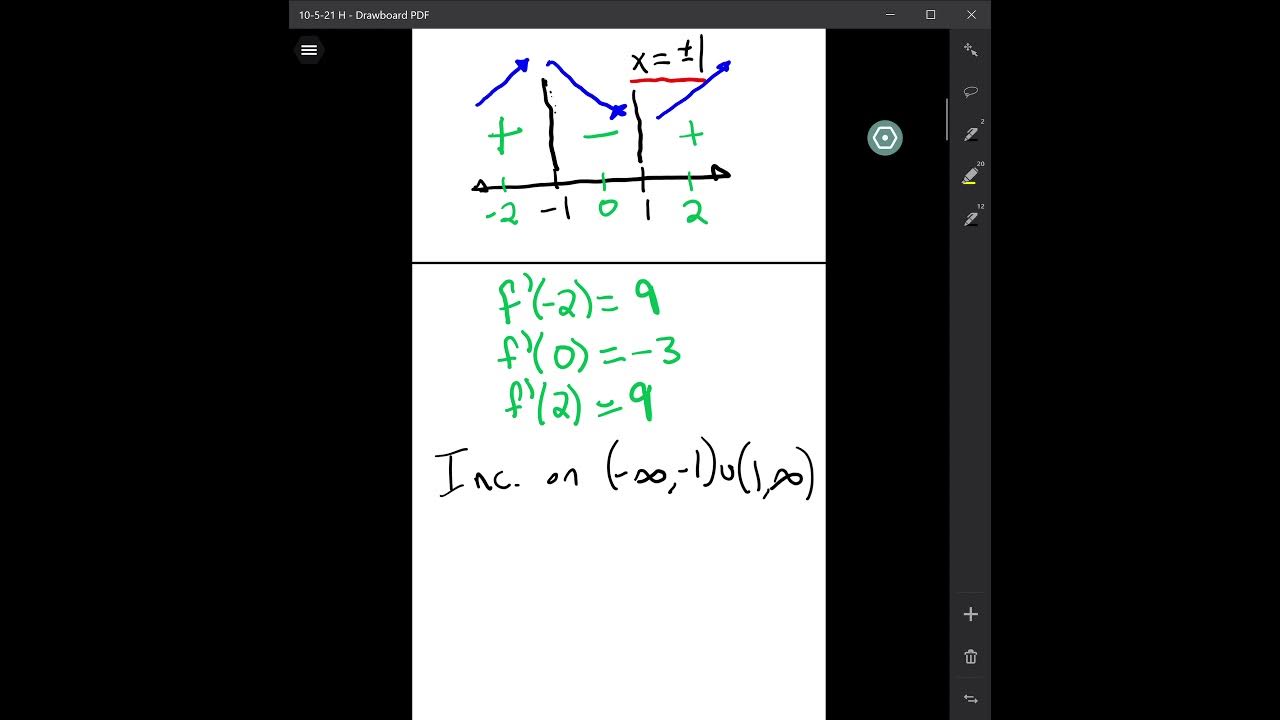
- 📊 A sign chart is used to determine where the function is increasing and decreasing by analyzing the sign of the first derivative in different intervals.
- 📌 The only critical point found is at x = 0, which corresponds to a local maximum since the function changes from increasing to decreasing at this point.
- 📝 The function is increasing on the intervals (-∞, -1) and (-1, 0), and decreasing on the intervals (0, 1) and (1, ∞), excluding the points where the function is undefined.
- 📑 The video concludes by reminding viewers to write down their answers after completing all the work, as having the work to justify the answer is not the same as directly answering the question.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is finding critical points of a function, including where the function is increasing and decreasing, and identifying local extrema.
Why is it important to consider the domain of a function when analyzing its behavior?
-It is important to consider the domain of a function because certain values of x may cause the function to be undefined, such as when the denominator of a rational function is zero. These points need to be excluded from the domain and from any analysis of increasing or decreasing intervals.
What are the domain restrictions for the function discussed in the script?
-The domain restrictions for the function are that x cannot be plus or minus one, as these values make the denominator of the function zero, which is undefined.
What is the horizontal asymptote of the given function and how can it be found?
-The horizontal asymptote of the given function is y equals one. It can be found by considering the behavior of the function as x approaches infinity or negative infinity.
What are the vertical asymptotes of the function and how can they be determined?
-The vertical asymptotes of the function are at x equals 1 and negative one. They can be determined by looking at the values of x that make the denominator of the function zero.
How can you find the y-intercept of the function?
-The y-intercept can be found by plugging in x equals zero into the function, which results in y equals zero, giving the point (0,0).
What is the process for finding the x-intercept of the function?
-To find the x-intercept, set the function equal to zero and solve for x. In the given function, multiplying both sides by the denominator and simplifying leads to x equals zero, which is the x-intercept.
What is the quotient rule and how is it used in the script to find the first derivative of the function?
-The quotient rule is a method used to find the derivative of a function that is the quotient of two other functions. In the script, it is used to find the first derivative of the given rational function by differentiating the numerator and denominator separately and applying the formula.
Why are the points x equals plus or minus one not considered critical points even though the derivative does not exist there?
-The points x equals plus or minus one are not considered critical points because these points are not in the domain of the original function, as they make the denominator zero. Critical points must be within the domain of the function.
How does the sign of the first derivative help determine where the function is increasing or decreasing?
-The sign of the first derivative indicates the slope of the function. If the derivative is positive, the function is increasing; if it is negative, the function is decreasing. By analyzing the sign of the derivative in different intervals, one can determine where the function has different behaviors.
What is the conclusion about the local extrema and intervals of increase and decrease for the function based on the script?
-The conclusion is that there is a local maximum at x equals zero, with no local minimum found. The function is increasing on the intervals (-∞, -1) and (-1, 0), and decreasing on the intervals (0, 1) and (1, ∞).
Outlines
📚 Introduction to Finding Critical Points and Extrema
This paragraph introduces the process of finding critical points and local extrema of a function. It emphasizes the importance of considering the domain of the function, especially where the denominator is zero, which leads to domain restrictions at x = ±1. The instructor also discusses the function's end behavior, which is related to asymptotes, and identifies a horizontal asymptote at y = 1 and vertical asymptotes at x = ±1. Additionally, the y-intercept is found to be at the origin (0,0), and the x-intercept is also at the origin, making it the only intercept. The paragraph concludes with a mention of finding critical points from the first derivative, which will be discussed in subsequent parts of the video.
🔍 Critical Points and Domain Considerations
The second paragraph delves into the specifics of finding critical points, highlighting the subtlety that points where the derivative does not exist (x = ±1) are not critical points since they are outside the domain of the original function. The focus then shifts to where the derivative is zero, leading to the identification of x = 0 as a critical point. The instructor also prepares to create a sign chart to determine where the function is increasing and decreasing, taking care to exclude the points where the function is undefined. The sign of the first derivative is analyzed across different intervals, revealing that the function has a local maximum at x = 0, with the value of the function at this point being 0.
📝 Summarizing Findings and Writing Answers
The final paragraph emphasizes the importance of not only doing the work to find critical points and determine where the function is increasing or decreasing but also of writing down the answers. The instructor provides a summary of the findings: a single critical point at x = 0, which is a local maximum with the function value being 0. The intervals on which the function is increasing are specified as (-∞, -1) and (-1, 0), and the intervals where the function is decreasing are given as (0, 1) and (1, ∞). The paragraph concludes with advice for students to ensure they write down their answers, as having the work to justify the answer is not the same as directly answering the question asked.
Mindmap
Keywords
💡Critical Points
💡Domain Restrictions
💡Increasing and Decreasing
💡Local Extrema
💡Asymptotes
💡Quotient Rule
💡Derivative
💡Sign Chart
💡Y-Intercept
💡X-Intercept
Highlights
Finding critical points where the function's increasing and decreasing, and local extrema.
Importance of considering the domain of the function even if not explicitly asked.
Domain restrictions due to the denominator being zero at x equals plus or minus one.
Exclusion of x equals 1 and negative 1 from the domain in intervals for increasing and decreasing.
End behavior of a rational function and its relation to asymptotes.
Identification of a horizontal asymptote at y equals one.
Presence of vertical asymptotes at x equals 1 and negative one.
Using limits to determine the behavior of the function around asymptotes.
Finding the y-intercept by plugging in x equals zero.
Determining the x-intercept and y-intercept to be at the origin (0,0).
Finding critical points by analyzing the first derivative using the quotient rule.
Simplification of the first derivative to identify critical points.
Clarification that x equals plus or minus one are not critical points due to domain restrictions.
Setting the derivative equal to zero to find critical points within the domain.
Identification of x equals zero as a critical point.
Using a sign chart to determine where the function is increasing and decreasing.
Analysis of the first derivative's sign in different intervals to find behavior of the function.
Conclusion that x equals zero is a local maximum with no local minimum found.
Writing down the intervals on which the function is increasing and decreasing.
Emphasis on the importance of writing down answers after completing all work.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: