Finding Binomial Probabilities Using the TI-84
TLDRThis educational video tutorial demonstrates how to use the TI-84 calculator to calculate binomial probabilities, an essential function for students. It clarifies the difference between the binomial PDF for exact values and the CDF for ranges, emphasizing the importance of correct input formatting. The instructor provides step-by-step examples, including calculating the probability of a specific number of successes and handling ranges using both PDF and CDF functions. The video also covers the use of the complement rule for 'at least' and 'at most' scenarios, offering practical tips to avoid common mistakes and simplify calculations.
Takeaways
- 🧮 The video demonstrates how to use a TI-84 calculator to calculate binomial probabilities, a crucial function for statistical analysis.
- 🔍 It clarifies the difference between the binomial PDF (probability density function) for exact values and the binomial CDF (cumulative distribution function) for ranges of values.
- 📝 The correct format for inputting data into the calculator for binomial PDF is total number of trials, probability of success, and the specific value being sought.
- 📊 For binomial CDF, the format includes the total number of trials, probability of success, and the highest value in the range being considered.
- 🔑 The importance of accuracy in selecting the right function (PDF vs. CDF) on the calculator is emphasized to avoid incorrect calculations.
- 📚 An example is provided where 70% of college students drink alcohol, and the task is to find the probability of exactly 10 out of 13 randomly selected students admitting to drinking.
- 🔄 A shortcut for the calculator is mentioned, where using the '2nd' and 'ENTER' keys can recall the last entry and allow for quick modifications, saving time.
- 📈 The video explains how to calculate the probability of 'at least' a certain number of successes by breaking it down into separate probabilities and using addition.
- 📉 The complement rule is introduced as a method to find probabilities for 'at least' or 'at most' scenarios by subtracting from 1 the probability of the complementary event.
- ✅ The video shows the correct use of the binomial CDF function on the calculator for finding probabilities of ranges, such as 'less than or equal to' a certain value.
- 📝 It also advises on converting open intervals into a format suitable for calculator input, ensuring the highest possible value is used for the calculation.
Q & A
What is the main topic of the video?
-The main topic of the video is how to use a TI-84 calculator to calculate binomial probabilities.
What are the two different functions for binomial calculations on the TI-84 calculator mentioned in the video?
-The two different functions mentioned are binomPDF and binomCDF.
What does the 'P' in binomPDF stand for?
-The 'P' in binomPDF stands for 'Probability' and it is used when looking for a specific random variable.
What does the 'CDF' in binomCDF stand for and when is it used?
-The 'CDF' in binomCDF stands for 'Cumulative Distribution Function' and it is used when looking for a range of successes.
How should you format the input for the binomPDF function on the TI-84 calculator?
-For the binomPDF function, you should first put the total number of trials, the probability of success, and then the value that you're trying to look for.
What is the significance of the third value in the binomCDF function?
-In the binomCDF function, the third value is the value that X has to be less than or equal to, which defines the range for the probability calculation.
What is an example scenario presented in the video for calculating binomial probabilities?
-An example scenario is calculating the probability that exactly ten out of thirteen randomly selected college students say they drink alcohol, given that 70% of college students drink alcohol.
How can you save time when changing the value you're looking for in the binomial calculation on the TI-84 calculator?
-You can save time by using the '2nd' key and then VARS (which brings up the distribution menu), and then pressing 'ENTER' to bring up the last entry and modify it.
What is the difference between calculating the probability of 'at least' a certain value using binomPDF and binomCDF?
-For 'at least' a certain value, binomPDF requires breaking down the problem into separate probabilities and adding them, while binomCDF can calculate the range directly if the last value entered is less than or equal to the value you're looking for.
How does the video demonstrate solving for a range of values in binomial probabilities?
-The video demonstrates solving for a range by converting an 'at most' or 'at least' scenario into a 'less than or equal to' format and using the binomCDF function to calculate the probability for that range.
What is the importance of the third value in the binomCDF function when calculating a range?
-The third value in the binomCDF function is crucial as it needs to be the highest possible value within the range you are looking for, ensuring the correct calculation of the probability for that range.
How does the video address the issue of negative scientific notation in probability calculations?
-The video explains that when dealing with negative scientific notation, you should write a point followed by the appropriate number of zeros (one less than the exponent) and then the significant digits, as seen in the example with '6.51e-4' being written as '0.000651'.
Outlines
🔢 Understanding Binomial Probabilities with TI-84 Calculator
This paragraph introduces the process of calculating binomial probabilities using a TI-84 calculator, highlighting the importance of formatting and the distinction between two functions: binomial PDF (for specific outcomes) and binomial CDF (for ranges of outcomes). The speaker emphasizes the correct input sequence for each function, which involves entering the total number of trials, the probability of success, and the value or range being sought. An example is given to illustrate the calculation of the probability that exactly ten out of thirteen randomly selected college students drink alcohol, using the binomial PDF function with the values 13 trials, 70% probability of success, and success value of 10, resulting in a probability of approximately 0.218. The speaker also demonstrates how to modify inputs for different scenarios, such as calculating the probability for exactly 13 successes, which yields a result of approximately 0.069.
📊 Calculating 'At Least' Probabilities with Binomial Functions
The second paragraph delves into calculating the probability of 'at least' a certain number of successes in a binomial distribution. The speaker explains how to break down the problem into separate probabilities for exact values and then sum them up. An example is provided where the probability of at least eleven out of thirteen college students drinking alcohol is calculated by adding the probabilities for exactly eleven, twelve, and thirteen successes, using the binomial PDF function. The speaker also contrasts this method with using the binomial CDF function, which simplifies the process by calculating the range directly. The paragraph also discusses the importance of correctly using the binomial PDF function to avoid errors and the utility of the CDF function in handling ranges, as demonstrated with the probability of fewer than four students drinking alcohol, rewritten as 'less than or equal to three' to fit the CDF function requirements.
🔍 Using Complement Rule and CDF for Range Probabilities
In this paragraph, the speaker discusses the use of the complement rule and the binomial CDF function to calculate probabilities for ranges, specifically 'at least' and 'at most' scenarios. The speaker shows how to rewrite a probability statement to fit the calculator's requirements and demonstrates the calculation of the probability that at least four out of thirteen students drink alcohol using the complement rule, which involves subtracting the probability of the complementary event (less than or equal to three students) from one. The speaker also explains how to calculate the probability of at most four students drinking alcohol directly using the binomial CDF function and contrasts it with the probability of more than four students, which is also found using the complement rule. The importance of using the correct function and input format is reiterated, with examples showing how to convert probabilities from scientific notation for ease of interpretation.
📚 Key Differences Between PDF and CDF for Binomial Calculations
The final paragraph summarizes the key differences between using the binomial PDF and CDF functions on the TI-84 calculator. The speaker clarifies that the PDF function is used for calculating exact values without a range, while the CDF function is used for finding probabilities within a range. It is emphasized that the third input in the CDF function should be the highest possible value within the range of interest. The speaker also advises on how to handle open intervals by converting them into a format that the calculator can process, such as changing 'less than' to 'less than or equal to' and adjusting the input values accordingly. This paragraph reinforces the importance of understanding the functions and input requirements to accurately calculate binomial probabilities.
Mindmap
Keywords
💡TI-84 Calculator
💡Binomial Probabilities
💡PDF (Probability Density Function)
💡CDF (Cumulative Distribution Function)
💡Total Number of Trials
💡Probability of Success
💡Specific Amount of Successes
💡Range of Successes
💡Complement Rule
💡Continuous vs. Discrete
Highlights
The video provides a tutorial on using the TI-84 calculator for binomial probability calculations.
There are two functions for binomial calculations: BINOMPDF for specific outcomes and BINOMCDF for ranges of outcomes.
BINOMPDF requires the total number of trials, success probability, and the specific success value to be inputted.
BINOMCDF also requires the total number of trials and success probability, but the last input is the highest value in the range.
An example is given where 70% of college students drink alcohol, and the probability of exactly 10 out of 13 saying they drink is calculated.
The probability for exactly 10 students is found using BINOMPDF with inputs 13, 0.7, and 10, resulting in approximately 0.218.
To find the probability for exactly 13 students, the last input is changed to 13, yielding approximately 0.069.
For calculating the probability of at least 11 students drinking, the video explains breaking it down into separate probabilities.
The sum of probabilities for 11, 12, and 13 students is calculated using BINOMPDF, resulting in approximately 0.202.
An alternate method for at least problems is introduced, using BINOMCDF for a range, which simplifies calculations.
The video demonstrates calculating the probability of less than four students drinking using BINOMCDF, rewriting the problem to fit the function.
The use of scientific notation in probability calculations is explained, with tips on handling negative exponents.
The complement rule is introduced as an easier way to calculate probabilities for 'at least' or 'at most' scenarios.
An example is shown where the probability of at least four students drinking is found using the complement rule, 1 - BINOMCDF(13, 0.7, 3).
The video concludes with a summary of the importance of using BINOMPDF for exact values and BINOMCDF for ranges, with correct input formatting.
Transcripts
Browse More Related Video
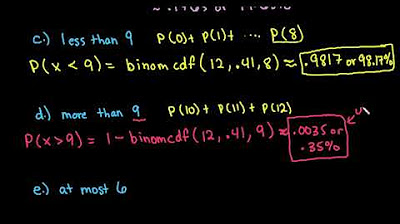
Binomial Probability with TI-84

Binomial Probability Using the TI-84

Finding The Probability of a Binomial Distribution Plus Mean & Standard Deviation

Using TI-84 to calculate binomial probability distribution
Finding Probabilities For A Binomial Distribution In StatCru

Normal Distribution: Calculating Probabilities {TI 84 Plus CE}
5.0 / 5 (0 votes)
Thanks for rating: