The Ferris Wheel - Trigonometric Function Model (1 of 3: Setting up the equation)
TLDRIn this educational video, the concept of using trigonometric functions to model real-world situations is explored. The focus is on the Ferris wheel, whose motion is modeled using a cosine function. The video provides a step-by-step guide on constructing an equation to represent the Ferris wheel's movement, taking into account its radius, period, and loading point. Through interactive technology like Desmos, viewers learn to adjust the function to accurately reflect the Ferris wheel's height above the ground and its complete rotation cycle, emphasizing the practical application of trigonometry in everyday scenarios.
Takeaways
- 📚 The lecture discusses the application of trigonometric functions to model real-world situations, such as oscillating phenomena.
- 📉 Trigonometric functions, specifically sine and cosine, are introduced as tools for modeling up and down or left and right movements.
- 🎢 The example of a Ferris wheel is used to illustrate how trigonometric functions can model the motion of objects.
- 📏 The radius of the Ferris wheel is given as 35 meters, which is a key parameter for constructing the model.
- ⏱ The Ferris wheel has a period of 90 seconds, which is the time taken for one complete rotation.
- 📍 The loading point of the Ferris wheel is 2 meters above the ground, which affects the starting position in the model.
- 🔧 The use of technology, specifically Desmos, is emphasized to construct and visualize the trigonometric model.
- 🔄 The cosine function is chosen to model the Ferris wheel's motion, starting with a basic cos(x) function.
- 📈 The model is adjusted to reflect the Ferris wheel's actual motion, including modifying the amplitude to represent the 35-meter radius.
- 📉 The amplitude adjustment involves multiplying by 35 and then adding 37 to ensure the motion is above ground level.
- 🔄 The concept of phase is briefly mentioned, hinting at further complexities that could be included in the model.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is the use of trigonometric functions to model real-world situations, specifically the motion of a Ferris wheel.
What are the examples given to illustrate the use of trigonometric functions in the script?
-Examples given include modeling electromagnetic radiation, tides, and temperatures, all of which involve oscillation that can be represented using trigonometric functions.
What is the radius of the Ferris wheel mentioned in the script?
-The radius of the Ferris wheel mentioned in the script is 35 meters.
What aspect of the trigonometric function describes the speed of motion?
-The aspect of the trigonometric function that describes the speed of motion is the period.
What is the period of the Ferris wheel's rotation mentioned in the script?
-The period of the Ferris wheel's rotation is 90 seconds.
What is the height of the loading point of the Ferris wheel from the ground?
-The loading point of the Ferris wheel is 2 meters above the ground.
Which trigonometric functions are suggested to model the up and down motion of the Ferris wheel?
-The sine and cosine functions are suggested to model the up and down motion of the Ferris wheel.
What is the initial approach to modifying the cosine function to fit the Ferris wheel's motion?
-The initial approach is to multiply the cosine function by 35 and then divide by 2 to adjust the amplitude of the motion.
What mistake is made in the initial attempt to adjust the cosine function, and how is it corrected?
-The mistake is that the Ferris wheel's motion goes below ground level. It is corrected by adding 35 to shift the motion above ground and then adding 2 to account for the loading point height.
Why is it important to understand the components of the trigonometric function equation in the context of the script?
-It is important to understand the components of the trigonometric function equation to interpret and construct models for real-world situations, such as the motion of the Ferris wheel, rather than just being handed the equation without understanding its meaning.
What tool is suggested for constructing the model of the Ferris wheel's motion?
-Desmos, an online graphing calculator, is suggested for constructing the model of the Ferris wheel's motion.
Outlines
📚 Introduction to Trigonometric Functions as Models
The video script begins with an introduction to the use of trigonometric functions as models for various real-world situations. The speaker mentions that these functions can model phenomena such as electromagnetic radiation and temperature changes, which involve oscillations. The main focus of the video is to demonstrate how trigonometric functions can be used to model the motion of a Ferris wheel. The speaker provides a brief overview of the concept and mentions the use of technology, specifically Desmos, to construct the model. Key details such as the radius of the Ferris wheel (35 meters) and its rotation period (90 seconds) are introduced, setting the stage for the modeling process.
🎡 Modeling the Ferris Wheel's Motion with Cosine Function
The second paragraph delves into the process of modeling the Ferris wheel's motion using the cosine function. The speaker guides the audience through adjusting the cosine function to match the Ferris wheel's characteristics, such as its radius and the fact that it does not operate underground. Initially, the cosine function is modified by multiplying by 35 and dividing by 2, which results in a range of motion from -17.5 to 17.5 meters, representing the radius. However, this leads to an issue where the Ferris wheel would go underground. The speaker then corrects this by adding 35 to the function, ensuring the motion stays above ground. Further adjustments are made by adding 2 meters to account for the loading point being 2 meters above the ground, which also implicitly includes the period of the Ferris wheel's rotation. The paragraph concludes with a correct model that reflects the Ferris wheel's motion without colliding with the ground and with the appropriate range of motion.
Mindmap
Keywords
💡Trigonometric functions
💡Modeling
💡Ferris wheel
💡Radius
💡Period
💡Loading point
💡Desmos
💡Sine and Cosine
💡Phase
💡Amplitude
💡Vertical axis (h-axis)
Highlights
Introduction to using trigonometric functions to model real-world situations.
Examples of modeling situations such as electromagnetic radiation and temperatures with trigonometric functions.
Focus on modeling the motion of a Ferris wheel using trigonometric functions.
Explanation of the radius of the Ferris wheel being 35 meters.
Description of the Ferris wheel's rotation period of 90 seconds.
Importance of the loading point being 2 meters above the ground.
Introduction of using technology, specifically Desmos, to construct the model.
Choice of cosine function to model the up and down motion of the Ferris wheel.
Adjustment of the cosine function to represent the height of the Ferris wheel over time.
Modification of the equation to reflect the Ferris wheel's radius of 35 meters.
Discussion on avoiding the Ferris wheel going underground by adjusting the equation.
Inclusion of the loading point's height in the model by adding 2 meters.
Ensuring the Ferris wheel does not collide with the ground by further adjusting the equation.
Explanation of how the period of the trigonometric function relates to the Ferris wheel's rotation.
Final adjustment of the model to accurately represent the Ferris wheel's motion without collision.
Emphasis on understanding the components of the trigonometric model rather than just interpreting it.
Engagement of the audience in problem-solving and model adjustment.
Transcripts
Browse More Related Video
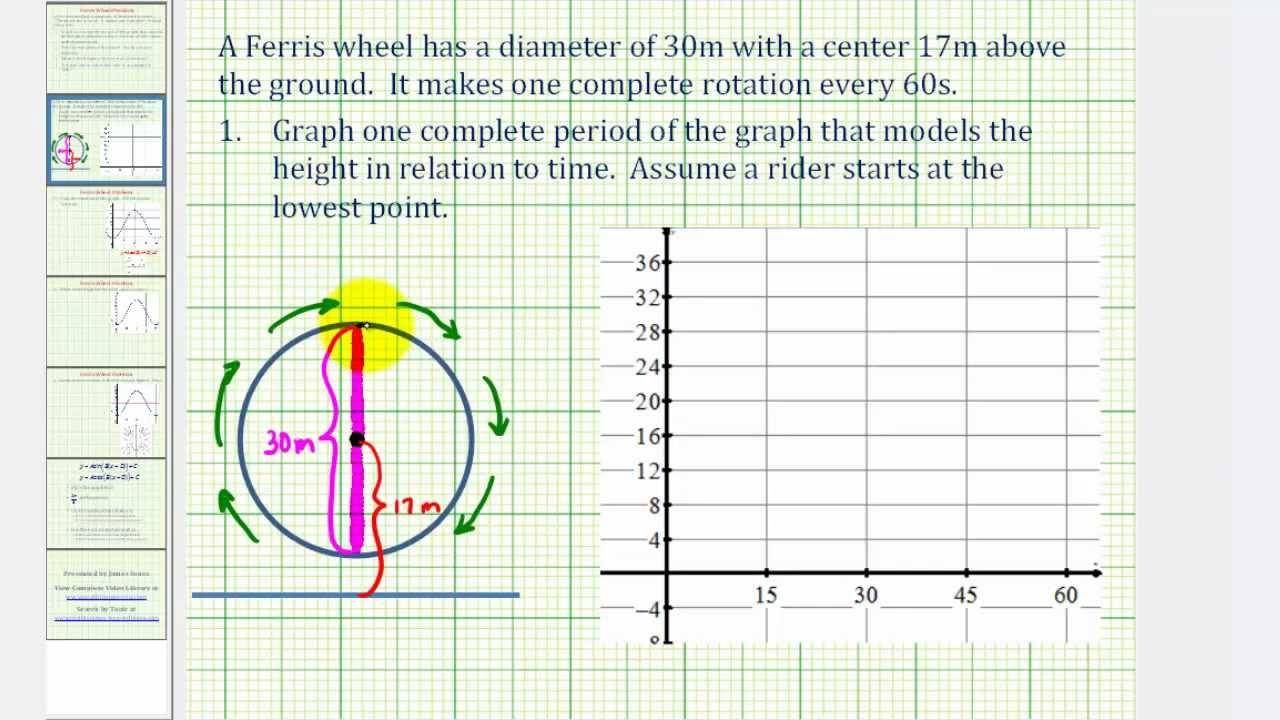
Ferris Wheel Trigonometry Problem

The Ferris Wheel - Trigonometric Function Model (3 of 3: Interpreting results)
Ferris Wheel Trig Problem

Ferris Wheel MHF4U Modelling Trigonometric Functions Test
Sinusoidal Function Word Problems: Ferris Wheels and Temperature

MCR3U - Word Problems for Sine and Cosine Functions
5.0 / 5 (0 votes)
Thanks for rating: