Solve eigen value in calculator

Smart Engineer
28 Dec 202010:13
EducationalLearning
32 Likes 10 Comments

TLDRThis instructional video script guides users on calculating the eigenvalues of a matrix using the fx991 ms calculator. It begins with resetting the calculator and storing a 3x3 matrix 'A' with specific elements. The script then explains how to derive the characteristic equation, involving lambda, the determinant, and the trace of matrix 'A'. It proceeds to demonstrate finding the determinant and inverse of 'A', and using these to calculate the eigenvalues. The video concludes with methods to verify the accuracy of the eigenvalues obtained, by checking if their sum equals the trace of 'A' and if their product equals the determinant of 'A', ensuring a correct solution.

Takeaways
  • πŸ”‹ Start by turning on and resetting the calculator to ensure no residual functions interfere.
  • πŸ“š Use the 'mod' button three times to access the matrix and vector functions on the fx991 ms calculator.
  • πŸ”’ Press 'number 2' to select the matrix function and prepare to input the matrix.
  • πŸ“ Store the matrix by pressing 'shift', '+', and 'number 4' to access 'dimension' and 'edit matrix'.
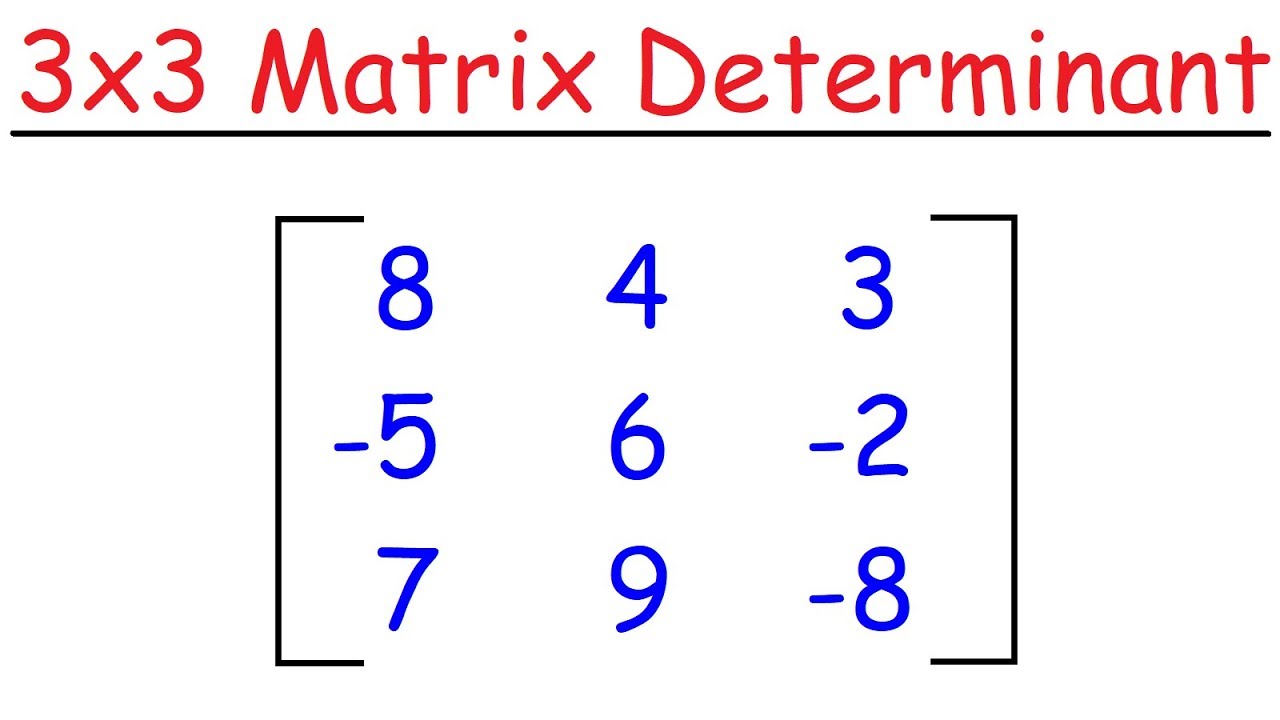
  • πŸ”‘ Name the matrix (e.g., 'A') and define its order, such as a 3x3 matrix for this example.
  • πŸ” Input the matrix elements sequentially, using 'plus' and 'equal to' to define each value.
  • πŸ“‰ Write the characteristic equation as lambda^3 - (trace of A)*lambda^2 + ... - determinant(A) = 0 for eigenvalues.
  • πŸ“Œ The trace of matrix A is the sum of its diagonal elements, which is 0 in the given example.
  • πŸ”Ž To find the determinant and inverse of matrix A, use the 'shift', '+', 'number 4' sequence on the calculator.
  • βœ… After calculating the determinant and inverse, use them to find the adjoint of A and construct the characteristic equation.
  • πŸ“ˆ Solve the characteristic equation to find the eigenvalues, which will be three in number for a 3x3 matrix.
  • πŸ” Validate the eigenvalues by checking if their sum equals the trace of A and if their product equals the determinant of A.
Q & A

  • How do I switch on and reset the calculator fx991 ms?

    -To switch on the calculator, simply power it up. To reset it, press 'Shift' followed by 'Mode', and then select the option '3 = =' to reset all functions.

  • Why is it necessary to reset the calculator before using it?

    -Resetting the calculator ensures that any previous functions or calculations do not interfere with the current task, providing a clean slate for new operations.

  • How do I store a matrix in the calculator fx991 ms?

    -To store a matrix, press 'Mod' three times to access 'Equation', 'Matrix', and 'Vector'. Then press '2' for matrix, and follow the prompts to input the matrix dimensions and elements.

  • What does the 'mat' icon on the calculator represent?

    -The 'mat' icon represents 'matrix', indicating that the calculator is in the matrix mode where you can input and manipulate matrices.

  • How do I name and define the order of a matrix in the calculator?

    -To name a matrix, press 'Shift' and 'Plus' followed by '4'. Then input the matrix name (e.g., 'A') and its order (e.g., 3x3 for a 3 by 3 matrix) using the provided options.

  • What is the general representation for entering elements of a 3x3 matrix?

    -The general representation involves entering the elements row by row, starting with the first row (a11, a12, a13), followed by the second row (a21, a22, a23), and then the third row (a31, a32, a33).

  • How do I check if the matrix values have been entered correctly in the calculator?

    -After entering the matrix, you can check the values by using the arrow keys to navigate through the matrix elements displayed on the screen.

  • What is the characteristic equation for a matrix and how is it derived?

    -The characteristic equation of a matrix is given by 'det(A - Ξ»I) = 0', where A is the matrix, Ξ» is the eigenvalue, and I is the identity matrix. A shortcut for a 3x3 matrix is 'Ξ»^3 - (trace of A)Ξ»^2 + ...', where the coefficients are derived from the matrix elements and its trace.

  • How can I find the determinant and inverse of a matrix using the calculator?

    -To find the determinant, press 'Shift', 'Plus', '4', then select '1' for determinant and 'A' for the matrix. To find the inverse, reset the calculator, access matrix mode, select matrix 'A', and use the 'x inverse' button under 'Mod' to calculate the inverse.

  • What is the relationship between the trace of a matrix and its eigenvalues?

    -The trace of a matrix, which is the sum of its diagonal elements, is equal to the sum of its eigenvalues. This relationship can be used to verify the correctness of the calculated eigenvalues.

  • How can I verify the correctness of the calculated eigenvalues?

    -You can verify the eigenvalues by checking if the sum of the eigenvalues equals the trace of the matrix and if the product of the eigenvalues equals the determinant of the matrix.

Outlines
00:00
πŸ”’ Matrix Eigenvalue Calculation with Calculator fx991 MS

The video provides a step-by-step guide on how to calculate the eigenvalue of a matrix using the fx991 MS calculator. It begins with the process of turning on and resetting the calculator to clear any previous functions. The user is then guided to store a matrix by pressing 'mod' three times to access the 'matrix and vector' option, selecting 'matrix' by pressing '2', and then entering the matrix dimensions and elements. The guide also explains how to check the matrix input for accuracy using the arrow keys. The video then moves on to deriving the characteristic equation for the matrix, which is essential for finding the eigenvalues. It simplifies the process by using a shortcut formula involving the determinant and trace of the matrix. The trace is calculated as the sum of the diagonal elements, and the determinant is found using the calculator's specific functions. The guide concludes with instructions on how to find the inverse of the matrix and multiply it by the determinant to obtain the adjoint matrix, which is crucial for the characteristic equation.

05:01
πŸ“š Solving for Eigenvalues and Verifying the Solution

This paragraph continues the tutorial by demonstrating how to find the inverse of matrix A using the calculator's 'x inverse' function and then multiplying it by the determinant to get the adjoint matrix. The diagonal elements of the adjoint matrix are summed to form the characteristic equation. The video then instructs the viewer to reset the calculator to clear the stored matrix values and solve the characteristic equation for the eigenvalues. It details the process of entering the coefficients of the characteristic equation into the calculator and solving for the eigenvalues, which in this case are found to be -2, 1, and 1. The video concludes with methods to verify the correctness of the calculated eigenvalues. It suggests checking if the sum of the eigenvalues equals the trace of the matrix and if the product of the eigenvalues equals the determinant of the matrix. If both conditions are met, it confirms that the eigenvalues are correct. The video emphasizes the importance of these checks during exams to ensure accuracy.

10:02
πŸ“ Cross-Checking Eigenvalue Calculations During Exams

The final paragraph of the script offers advice on how to efficiently verify eigenvalue calculations during an exam using a calculator. It suggests that students should use the calculator's functions to cross-check their answers by ensuring the sum of the eigenvalues matches the trace of the matrix and that the product of the eigenvalues equals the determinant. This quick verification step can help confirm the correctness of the eigenvalue calculations, providing confidence in the exam setting.

Mindmap
Keywords
πŸ’‘Eigenvalue
An eigenvalue is a scalar value that, when a matrix is multiplied by a non-zero vector, results in a scaled version of the same vector. It is a key concept in linear algebra and is used to understand the properties of a matrix. In the video's context, the eigenvalue is calculated to analyze the matrix using the calculator fx991 ms, as part of the process to find the characteristic equation and solve for 'lambda'.
πŸ’‘Matrix
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. It is a fundamental object in various areas of mathematics. In the video, the matrix is the central object being manipulated to find its eigenvalues, with specific steps provided for inputting and storing it in the calculator.
πŸ’‘Calculator fx991 ms
The fx991 ms is a scientific calculator that is used in the video for performing complex mathematical operations, such as finding eigenvalues of a matrix. The script provides a step-by-step guide on how to use this calculator to reset, store matrices, and perform calculations related to eigenvalues.
πŸ’‘Reset
In the context of the video, 'reset' refers to the action of clearing the calculator's memory and settings to a default state. This is important before starting a new calculation to ensure that no residual data from previous operations interferes with the current task of finding eigenvalues.
πŸ’‘Characteristic Equation
The characteristic equation of a matrix is a polynomial equation that is derived from the matrix and is used to find its eigenvalues. In the script, the characteristic equation is mentioned as 'lambda cube minus lambda square plus lambda minus determinant of A equals zero', which simplifies to finding the roots of this equation to determine the eigenvalues.
πŸ’‘Determinant
The determinant is a scalar value that can be computed from the elements of a square matrix and encodes certain properties of the linear transformation described by the matrix. In the video, the determinant is calculated using the calculator to help in forming the characteristic equation and ultimately finding the eigenvalues.
πŸ’‘Trace
The trace of a square matrix is the sum of the elements on its main diagonal (from top left to bottom right). It is used in the script to find the coefficient of lambda in the characteristic equation, which is the sum of the diagonal elements of the matrix.
πŸ’‘Adjoint
The adjoint of a matrix is the transpose of the cofactor matrix. It is used in the script to find the inverse of a matrix, which is then used in the calculation of the eigenvalues. The adjoint is also related to the characteristic equation through the determinant.
πŸ’‘Inverse
The inverse of a matrix is another matrix that, when multiplied with the original matrix, yields the identity matrix. In the video, the inverse of the matrix is calculated to help in forming the adjoint matrix, which is essential for solving the characteristic equation.
πŸ’‘Solving Equation
Solving an equation involves finding the values of the variables that make the equation true. In the context of the video, solving the equation refers to finding the eigenvalues (lambda) by solving the characteristic equation, which is a third-degree polynomial equation.
πŸ’‘Verification
Verification in the script refers to the process of checking the correctness of the calculated eigenvalues. This is done by comparing the sum and product of the eigenvalues with the trace and determinant of the matrix, respectively. If the calculated values align with these properties, it confirms the accuracy of the eigenvalues found.
Highlights

Introduction to finding eigenvalues of a matrix using the calculator fx991 ms.

Instructions to switch on and reset the calculator for a fresh start.

Explanation of how to access the matrix storage function on the calculator.

Step-by-step guide to inputting a matrix into the calculator.

Description of the matrix dimension and naming process.

Entering the elements of a 3x3 matrix into the calculator.

Verification of matrix entry through the calculator's interface.

Introduction to the characteristic equation and its relation to eigenvalues.

Shortcut for deriving the characteristic equation.

Explanation of the trace of a matrix and its role in the characteristic equation.

Method to find the determinant of a matrix using the calculator.

Process to calculate the inverse of a matrix on the calculator.

Combining the inverse matrix with the determinant to find the adjoint.

Calculation of the trace of the adjoint matrix.

Formation of the characteristic equation using calculated values.

Instructions to reset the calculator for solving the equation.

Solving the characteristic equation for eigenvalues on the calculator.

Verification of eigenvalues by checking the sum and product against the matrix's trace and determinant.

Final validation of eigenvalues using the calculator for accuracy.

Transcripts

Browse More Related Video

21. Eigenvalues and Eigenvectors

Inverse of 3x3 matrix

Inverse of a 3x3 Matrix | Co-factor Method

How to Invert Matrices - Exercises (Step by Step)

How To Find The Determinant of a 3x3 Matrix

Inverse of a 3x3 Matrix - (THE SIMPLE WAY)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix CalculationEigenvalue TutorialCalculator Guidefx991 MSMathematicsEducational ContentTech TutorialEngineering MathScience EducationCalculus Tools