ANGLES IN A UNIT CIRCLE || PRE-CALCULUS
TLDRThis video lesson, hosted by Mark Awamat, delves into the concept of angles within a unit circle in the realm of trigonometry. It explains that an angle is formed by two rays sharing a common endpoint and discusses how angles are measured in terms of rotation around this point. The video covers the distinction between clockwise and counterclockwise rotations, with clockwise rotations yielding negative angles and counterclockwise rotations resulting in positive angles. It also explores the Babylonian sexagesimal system, which underpins our modern understanding of degrees, minutes, and seconds for measuring angles. The lesson provides step-by-step instructions on converting between degrees, minutes, and seconds, as well as converting these measurements into decimal degrees. Practical examples are given to illustrate the conversion process, ensuring that viewers can grasp the method and apply it to various scenarios. The video concludes with a reminder to like, subscribe, and enable notifications for more educational content.
Takeaways
- 📚 An angle in geometry is defined as the union of two non-collinear rays sharing a common endpoint.
- 🔄 In trigonometry, angles are viewed as the amount of rotation about their endpoint, requiring labeling of the initial and terminal sides.
- 🌀 The direction of rotation affects angle measurement; counter-clockwise rotation is positive, while clockwise is negative.
- 🔢 A full rotation (360 degrees) is equivalent to 60 minutes, and one minute is equivalent to 60 seconds, based on the sexagesimal system.
- 📐 Angles can be converted from decimal degrees to degrees, minutes, and seconds (DMS), and vice versa.
- ➡️ To convert from decimal degrees to DMS, multiply the decimal part by 60 to get minutes, and the decimal part of minutes by 60 to get seconds.
- 🔍 To convert DMS to decimal degrees, convert minutes to a decimal by dividing by 60, and add this to the degrees.
- 📈 The Babylonians developed the degree measure around 2000 BC, which is based on a sexagesimal (base 60) numeration system.
- 📉 Negative angles represent clockwise rotation, while positive angles represent counter-clockwise rotation.
- 📝 Examples are provided in the script to demonstrate the conversion process between decimal degrees and DMS.
- 👍 The video aims to educate viewers on how to convert angle measurements and encourages engagement through likes, subscriptions, and notifications.
Q & A
What is an angle in the context of geometry?
-In geometry, an angle is defined as the union of two non-collinear rays which have the same endpoint. The angle measures are restricted between 0 degrees and 180 degrees inclusive or exclusive.
How is an angle defined in trigonometry?
-In trigonometry, an angle is viewed as the amount of rotation generated when a ray is rotated about its endpoint. It is necessary to label the side of an angle as the initial side and the terminal side.
What are the initial and terminal sides of an angle?
-The initial side of an angle is the position of the ray at the start of its rotation, and the terminal side is the position of the ray at the end of its rotation.
How does the direction of rotation affect angle measures?
-The direction of rotation affects angle measures because a counter-clockwise rotation results in a positive angle measure, while a clockwise rotation results in a negative angle measure.
What is a full rotation or revolution equivalent to in degrees?
-A full rotation or revolution is equivalent to 360 degrees.
How is a degree measure related to minutes and seconds?
-A degree measure is related to minutes and seconds as 1 degree is equal to 60 minutes, and 1 minute is equal to 60 seconds.
How can you convert a decimal degree to minutes and seconds?
-To convert a decimal degree to minutes and seconds, you multiply the decimal part by 60 to get minutes, and then multiply any remaining decimal part by 60 to get seconds.
What is the Babylonian sexagesimal numeration system?
-The Babylonian sexagesimal numeration system is a base-60 number system used for measuring angles, where a complete rotation or revolution is equivalent to 360 degrees.
How can you convert minutes and seconds back to decimal degrees?
-To convert minutes and seconds back to decimal degrees, you convert the minutes to a fraction of a degree by dividing by 60, and then add the seconds converted to a fraction of a degree by dividing by 3600 (60 minutes * 60 seconds).
Can you provide an example of converting 31 degrees 12 minutes and 54 seconds to decimal degrees?
-Yes, to convert 31 degrees 12 minutes and 54 seconds to decimal degrees, you would calculate 54 seconds as 0.9 minutes (54 * 1/60), add this to 12 minutes to get 12.9 minutes, and then convert 12.9 minutes to degrees by dividing by 60, which gives 0.215 degrees. Adding this to 31 degrees results in 31.215 degrees.
How can you convert negative angle measurements like -5 degrees 48 minutes 41 seconds to decimal degrees?
-To convert negative angle measurements to decimal degrees, you first convert the minutes and seconds to a decimal form, then add it to the degrees. For example, -5 degrees 48 minutes 41 seconds would be calculated as -5 + (48 + 41/60)/60 degrees, resulting in -5.81 degrees.
Outlines
📚 Introduction to Angles in a Unit Circle
In this video lesson, Mark Awamat introduces the concept of angles in a unit circle from a trigonometric perspective. He explains that an angle is the union of two non-collinear rays sharing a common endpoint, traditionally measured between 0 and 180 degrees. However, in trigonometry, angles are considered as the amount of rotation around this endpoint, necessitating the labeling of the initial and terminal sides of the angle. The direction of rotation, either clockwise or counterclockwise, also affects the angle's measure, with clockwise rotations resulting in negative angles and counterclockwise in positive ones. The video also touches on the Babylonian development of the degree measure around 2000 BC, based on a sexagesimal system.
🔍 Converting Decimal Degrees to Minutes and Seconds
The second paragraph delves into the conversion of decimal degrees to degrees, minutes, and seconds. Awamat illustrates this by converting 22.4 degrees into 22 degrees and 24 minutes. He further explains the sexagesimal system, where 1 degree equals 60 minutes and 1 minute equals 60 seconds. Another example is given for 14.21 degrees, which is broken down into 14 degrees, 12 minutes, and 36 seconds. The process involves multiplying the decimal part of the degree by 60 to get minutes and then taking the decimal part of the minutes to get seconds, ensuring a clear understanding of the conversion process.
📐 Converting Degrees, Minutes, and Seconds to Decimal Degrees
In the third paragraph, the focus shifts to converting measurements given in degrees, minutes, and seconds back into decimal degrees. Awamat provides a step-by-step method to convert 31 degrees 12 minutes and 54 seconds into 31.215 degrees. The process involves converting seconds to minutes by multiplying by 1/60, then adding this to the minutes and converting the sum to degrees by multiplying by 1/60 again. Additional examples include converting 50 degrees 22 minutes and 11 seconds into 70.37 degrees and -5 degrees 48 minutes and 41 seconds into -5.81 degrees, demonstrating the application of the method for both positive and negative angle measurements.
🎓 Conclusion and Call to Action
The final paragraph serves as a conclusion and a call to action for the viewers. It briefly reminds the audience of the key points covered in the video and encourages them to continue learning. The host also prompts viewers to like, subscribe, and hit the bell button for updates on more video tutorials. This closing remark is designed to engage the audience and keep them coming back for more educational content.
Mindmap
Keywords
💡Angle
💡Unit Circle
💡Degrees
💡Trigonometry
💡Rotation
💡Terminal Side
💡Initial Side
💡Degrees, Minutes, Seconds
💡Sexagesimal System
💡Conversion
Highlights
Introduction to angles in a unit circle and their definition in geometry.
Explanation of angle measures restricted between 0 and 180 degrees.
Discussion of angles as the amount of rotation in trigonometry.
Importance of labeling the initial and terminal sides of an angle.
Impact of the direction of rotation on angle measures.
Examples of positive and negative angle measures.
Historical development of the degree measure by the Babylonians.
Conversion of a complete rotation to 360 degrees based on the sexagesimal system.
Explanation of the relationship between degrees, minutes, and seconds.
Conversion of decimal degrees to minutes and seconds.
Illustration of converting 22.4 degrees to minutes and seconds.
Process of converting 14.21 degrees to degrees, minutes, and seconds.
Conversion of degree measurements to decimal degrees.
Example of converting 31 degrees 12 minutes and 54 seconds to decimal degrees.
Conversion of 50 degrees 22 minutes and 11 seconds to decimal degrees.
Demonstration of converting negative angle measurements to decimal degrees.
Final summary of converting degree measurements to decimal degrees.
Encouragement to like, subscribe, and hit the bell button for more video tutorials.
Transcripts
Browse More Related Video
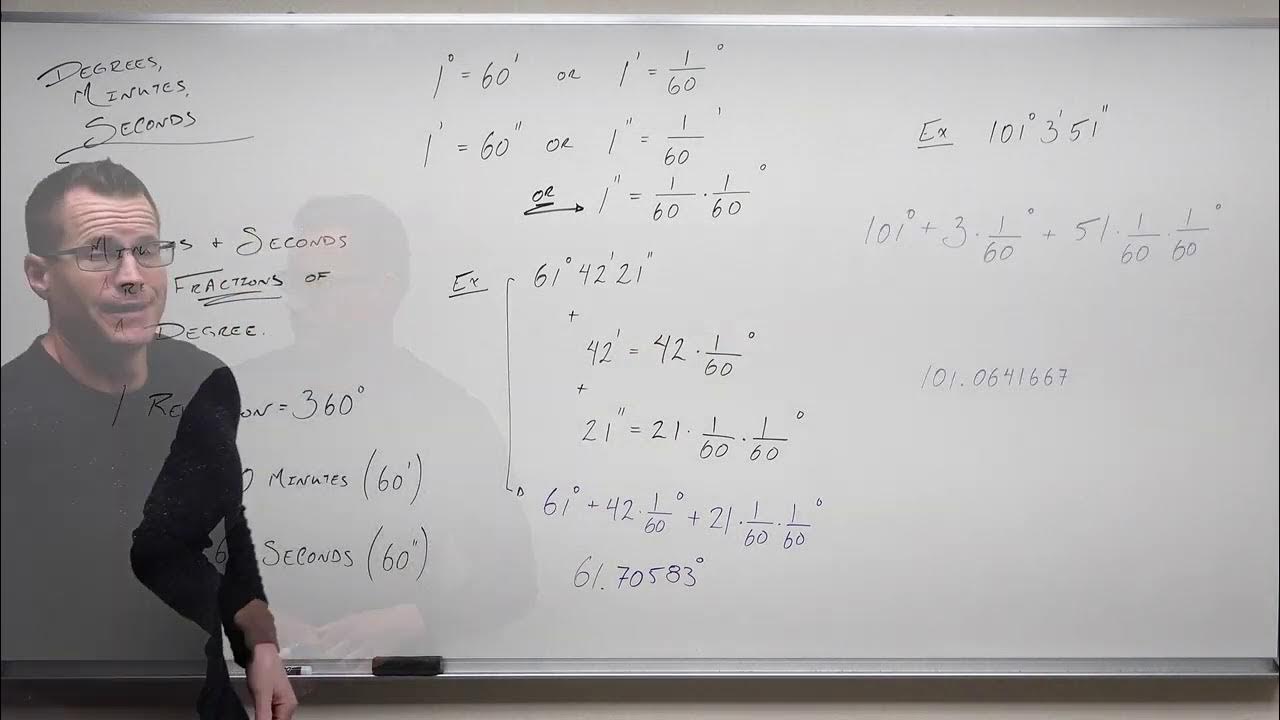
Converting Degrees, Minutes, and Seconds (Precalculus - Trigonometry 2)

How To Find The Reference Angle In Radians and Degrees - Trigonometry

REFERENCE ANGLES || PRE-CALCULUS

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS
Coterminal Angles In Radians & Degrees - Basic Introduction, Trigonometry

Bearings In Maths
5.0 / 5 (0 votes)
Thanks for rating: