Converting Degrees, Minutes, and Seconds (Precalculus - Trigonometry 2)

Professor Leonard

2 Feb 202119:09

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video delves into the concept of degrees, minutes, and seconds as units of angular measurement. It explains that a full rotation is 360 degrees, and to measure smaller angles, we use minutes and seconds, where one degree equals 60 minutes and one minute equals 60 seconds. The video demonstrates how to convert between these units and decimal degrees, emphasizing the precision these units offer, especially in fields like trajectory analysis. It also touches on the importance of understanding the quadrant of the angle being measured. The host guides viewers through examples of converting both from and to degrees, minutes, and seconds, and concludes by previewing the next topic: radians, a different unit of angular measure that will be explored in an upcoming video.

Takeaways

📏 Degrees, minutes, and seconds are units used to measure angles more precisely than just degrees alone.
🔄 One full rotation is 360 degrees, which can be further divided into 60 minutes and 60 seconds each for more specificity.
↔️ To convert between degrees, minutes, and seconds, you can use mathematical conversions: 1 degree = 60 minutes, 1 minute = 60 seconds.
🔢 Decimals are also used to measure angles but degrees, minutes, and seconds are particularly useful for very precise measurements.
⚙️ The conversion process involves multiplying minutes and seconds by 1/60 of a degree to convert them into decimal degrees.
⛓ When converting from decimal degrees to degrees, minutes, and seconds, you multiply the decimal part by 60 to find the minutes and then the remaining decimal by 60 to find the seconds.
📐 The term 'minutes of angle' refers to the specific measurement of angles in minutes, which is a very precise way to express angular measurements.
🚫 If during conversion you end up with more than 60 seconds or minutes, it indicates a mistake as these units are fractions of a degree or minute, respectively.
🧮 The base-60 system used in degrees, minutes, and seconds can be contrasted with the base-10 system used in decimal measurements.
📈 Degrees, minutes, and seconds allow for exceptionally small and precise measurements of angles, which are valuable in various fields like navigation and astronomy.
➡️ The script also hints at the upcoming discussion about radians, another unit for measuring angles that is particularly useful in calculus and other mathematical contexts.

Q & A

What is the significance of degrees, minutes, and seconds in measuring angles?
-Degrees, minutes, and seconds are units used to measure angles with a high degree of precision. They allow for the expression of angles in very small increments, which is particularly useful in fields such as navigation, surveying, and astronomy.
How many degrees are there in a full rotation?
-A full rotation is 360 degrees.
What is the relationship between degrees, minutes, and seconds?
-One degree is equal to 60 minutes, and one minute is equal to 60 seconds. This is a base-60 system used to measure smaller fractions of a degree.
Why might someone choose to use minutes and seconds instead of decimal degrees?
-While decimal degrees are often used for convenience in calculations, minutes and seconds are still commonly used in certain contexts, such as navigation and legal land descriptions, because they can provide a more precise and unambiguous representation of an angle.
How can you convert minutes into a decimal form of degrees?
-To convert minutes into decimal degrees, you multiply the number of minutes by 1/60, since there are 60 minutes in one degree.
What is the conversion factor from seconds to minutes?
-There are 60 seconds in one minute, so to convert seconds into minutes, you multiply the number of seconds by 1/60.
How do you convert a decimal degree measurement into minutes and seconds?
-First, you separate the whole number of degrees from the decimal fraction. The decimal fraction, when multiplied by 60, gives you the minutes. Then, take the decimal fraction of the minutes and multiply by 60 to get the seconds.
What happens if the calculated minutes or seconds exceed 60 when converting from decimal degrees?
-If the calculated minutes or seconds exceed 60, it indicates an error in the conversion process. Each minute should be less than 60, and each second should be less than 60 as well.
How can you determine the quadrant of an angle given in degrees, minutes, and seconds?
-The quadrant of an angle can be determined by looking at the whole number of degrees. For example, angles between 0 and 90 degrees are in the first quadrant, while angles between 90 and 180 degrees are in the second quadrant.
Why are radians used in calculus and other mathematical contexts?
-Radians are used because they provide a more natural unit for measuring angles, especially in calculus. Many mathematical formulas and operations are more straightforward and elegant when expressed in terms of radians.
What is the conversion factor from degrees to radians?
-Radians are a different unit of angle measurement. To convert degrees to radians, you multiply the number of degrees by π/180, because a full circle is 2π radians.
How can you convert an angle from degrees, minutes, and seconds to a decimal degree representation?
-First, convert the minutes to a decimal by dividing by 60. Then, convert the seconds to a decimal by dividing by 3600 (since there are 60 seconds in a minute and 60 minutes in a degree). Add these decimal values to the whole number of degrees to get the decimal degree representation.

Outlines

00:00

📏 Understanding Degrees, Minutes, and Seconds

This paragraph introduces the concept of degrees, minutes, and seconds as a way to measure angles with precision smaller than one degree. It explains that a full rotation is 360 degrees, and to measure smaller increments, we use minutes (1/60th of a degree) and seconds (1/60th of a minute). The paragraph also touches on the use of decimals as an alternative but emphasizes the prevalence and importance of minutes and seconds in precision measurements, especially in fields like trajectory studies.

05:00

🔢 Converting Between Minutes, Seconds, and Decimal Degrees

The second paragraph delves into how to convert between minutes and seconds of a degree into decimal form and vice versa. It explains that one minute is equal to 1/60th of a degree and one second is 1/60th of a minute, leading to the conversion factor of 1/3600th of a degree for seconds. The paragraph provides a step-by-step method for converting angle measurements, emphasizing the importance of unit consistency during calculations and the accuracy achievable with this system.

10:02

🧮 Quadrants and Reverse Conversion from Decimal Degrees

This paragraph discusses the process of identifying the quadrant of an angle and then reverse converting decimal degrees into minutes and seconds. It clarifies that even with minutes and seconds, the primary identifier for the quadrant is the degree value. The paragraph also provides a method for converting decimal degrees to degrees, minutes, and seconds by multiplying the decimal part by 60 to get minutes and then further multiplying any decimal minutes by 60 to get seconds, rounding as necessary.

15:02

🔄 Further Practice and Transition to Radians

The final paragraph encourages further practice in converting between different units of angle measurement and hints at the next topic of discussion: radians. It emphasizes the importance of understanding where minutes and seconds come from and how they are used. The paragraph concludes by previewing the next video, which will cover radians as an alternative unit for measuring angles, particularly useful for calculus and other advanced mathematical applications.

Mindmap

Keywords

💡Degrees

Degrees are a unit of measurement used to express angles, with one full rotation being equal to 360 degrees. In the context of the video, degrees are the starting point for understanding more precise measurements of angles through minutes and seconds. An example from the script is 'one degree is one 360th of a rotation.'

💡Minutes

Minutes are a subdivision of a degree, where one degree is equivalent to 60 minutes. They are used to measure angles with more specificity than whole degrees. The script illustrates this by stating 'one degree is equal to 60 minutes' and explains how to convert minutes into a decimal form of degrees.

💡Seconds

Seconds are an even smaller unit of angle measurement, with one minute being divided into 60 seconds. They allow for extremely precise angle measurements. The video uses the conversion of seconds to degrees to demonstrate this precision, as in 'one second equals one sixtieth of a minute.'

💡Decimal Degrees

Decimal degrees are a way to express angles in a continuous numeric value rather than in the discrete units of degrees, minutes, and seconds. The video discusses converting between the traditional DMS (degrees, minutes, seconds) format and decimal degrees for convenience and compatibility with certain calculations, as shown by the conversion example '61 degrees plus ... portion as a degree.'

💡Rotation

A rotation refers to a full circular movement, which is 360 degrees. The concept is fundamental to understanding how degrees, minutes, and seconds are used to describe the magnitude of an angular rotation. The script mentions 'one roll full rotation from an initial side to a terminal side.'

💡Conversion

Conversion in the context of the video means translating measurements from one system to another, such as from degrees, minutes, and seconds to decimal degrees, or vice versa. It is a key process demonstrated in the video to show how different units of angular measurement can be interchanged, as in 'how to convert between the minutes and seconds fractions of a degree and decimal portions of that same degree.'

💡Quadrant

A quadrant is one of the four equal parts of a circle, each representing 90 degrees. The video mentions quadrants in relation to the terminal side of an angle, emphasizing that even when using degrees, minutes, and seconds, one can still determine the quadrant of the angle, as stated 'we should still be able to determine the quadrant in which our angles reside.'

💡Base 60

Base 60, also known as sexagesimal, is the number system used for measuring angles in degrees, minutes, and seconds. The video explains that because the system is base 60, one minute is 60 seconds and one degree is 60 minutes, as mentioned 'we don't have a base 10 we have a base 60.'

💡Radians

Radians are another unit for measuring angles, which will be discussed in a subsequent video as per the script. They are particularly useful in calculus and other mathematical contexts where formulas are more elegantly expressed using radians. The video teaser suggests 'we're going to talk about how we can measure that a different way we can measure with some angles with something called radians.'

💡Terminal Side

The terminal side of an angle is the side that terminates or ends after a certain number of degrees of rotation from the initial side. The concept is important for understanding the orientation of angles within a circle. The script uses this term to describe the final position after a full rotation, as in 'terminates where it begins, where it starts or terminates.'

💡Trajectory

Trajectory refers to the path that an object follows through space as a result of its launch or motion. In the video, it is mentioned in the context of using minutes of angle to describe the precise path or direction of something in motion, as stated 'if you've ever studied trajectory, minutes of angle is what they're talking about.'

Highlights

Degrees, minutes, and seconds are used to measure angles smaller than one degree.

A full rotation is 360 degrees, which can be further divided into minutes and seconds for precision.

One degree is equal to 60 minutes, and one minute is equal to 60 seconds.

Degrees, minutes, and seconds are fractions of a degree, allowing for very precise angle measurements.

Decimals are often used for convenience, but minutes and seconds are common in certain fields like trajectory studies.

Conversion between minutes and seconds to decimal degrees and vice versa is demonstrated through examples.

One minute is equal to one-sixtieth of a degree, and one second is one-sixtieth of a minute.

One second is equivalent to one over 3600 of a degree, which is an exceptionally small unit of measurement.

The video provides a method to convert minutes and seconds into decimal degrees by multiplying by 1/60.

When converting from decimal degrees to minutes and seconds, the process involves multiplying by 60.

If the calculated degrees exceed 60, it indicates an error in the conversion process.

The video emphasizes the importance of understanding the quadrant in which the angle terminates.

An example is given to convert 18.255 degrees into minutes and seconds, illustrating the process.

The distinction between degrees, minutes, and seconds is valuable for accuracy, despite the preference for decimal notation.

The video concludes with a teaser for the next topic, which is radians, a different unit for measuring angles.

Radians are especially useful in calculus and many formulas are more straightforward when using radians instead of degrees.

The video encourages practice and understanding of the conversion process between degrees, minutes, seconds, and decimals.

Transcripts

Browse More Related Video

ANGLES IN A UNIT CIRCLE || PRE-CALCULUS

Converting Radians and Degrees (Precalculus - Trigonometry 4)

MOA vs. MRAD in Scope Adjustments

CONVERTING DEGREE MEASURE TO RADIAN MEASURE AND VICE VERSA || PRE-CALCULUS

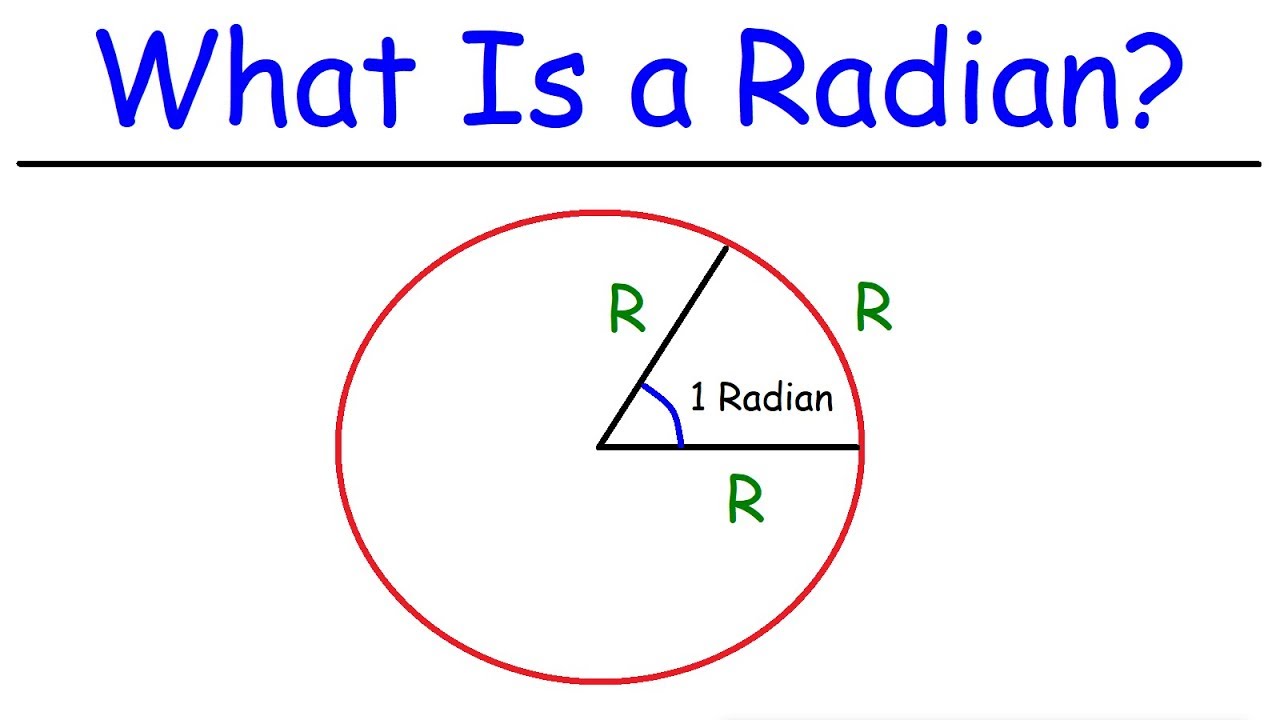
Trigonometry - What Exactly Is a Radian?

Decimal Degrees to DMS Formula - Converting Degrees Minutes and Seconds to Decimal - Trigonometry

Converting Degrees, Minutes, and Seconds (Precalculus - Trigonometry 2)

Takeaways

Q & A

What is the significance of degrees, minutes, and seconds in measuring angles?

How many degrees are there in a full rotation?

What is the relationship between degrees, minutes, and seconds?

Why might someone choose to use minutes and seconds instead of decimal degrees?

How can you convert minutes into a decimal form of degrees?

What is the conversion factor from seconds to minutes?

How do you convert a decimal degree measurement into minutes and seconds?

What happens if the calculated minutes or seconds exceed 60 when converting from decimal degrees?

How can you determine the quadrant of an angle given in degrees, minutes, and seconds?

Why are radians used in calculus and other mathematical contexts?

What is the conversion factor from degrees to radians?

How can you convert an angle from degrees, minutes, and seconds to a decimal degree representation?