Calculus 2 Lecture 10.2: Introduction to Parametric Equations

Professor Leonard

1 May 201498:26

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the concept of parametric equations in detail, emphasizing their importance in describing the motion of an object on a plane. The instructor explains the challenges of defining plain curves using traditional rectangular coordinates and introduces parametric equations as a solution. By using an independent variable, typically time (T), both X and Y coordinates can be expressed, allowing for a clear depiction of the object's starting point, path, and direction. The video provides several examples to illustrate how to plot points, determine the initial and terminal points, and establish the trajectory's orientation. The use of trigonometric identities is highlighted to simplify the equations and predict the shape of the curve, such as circles and ellipses. The video is an informative guide for those seeking to understand the fundamentals of parametric equations and their application in calculus.

Takeaways

📚 The discussion introduces parametric equations as a method to describe the motion of an object on a plane, which is not always possible using traditional Cartesian coordinates.
🌐 Parametric equations are defined using a parameter (commonly denoted as 't' or 'θ'), allowing x and y coordinates to be expressed as functions of this parameter.
🔄 The parameter represents a variable independent of x and y, and is often conceptualized as time, although it doesn't strictly have to be time.
📈 The script outlines the process of converting parametric equations into a graphical representation, emphasizing the importance of understanding the object's starting point, terminal point, and direction of motion.
🤔 Challenges with defining plane curves using traditional functions are highlighted, such as the inability to explicitly define some curves in terms of a single variable.
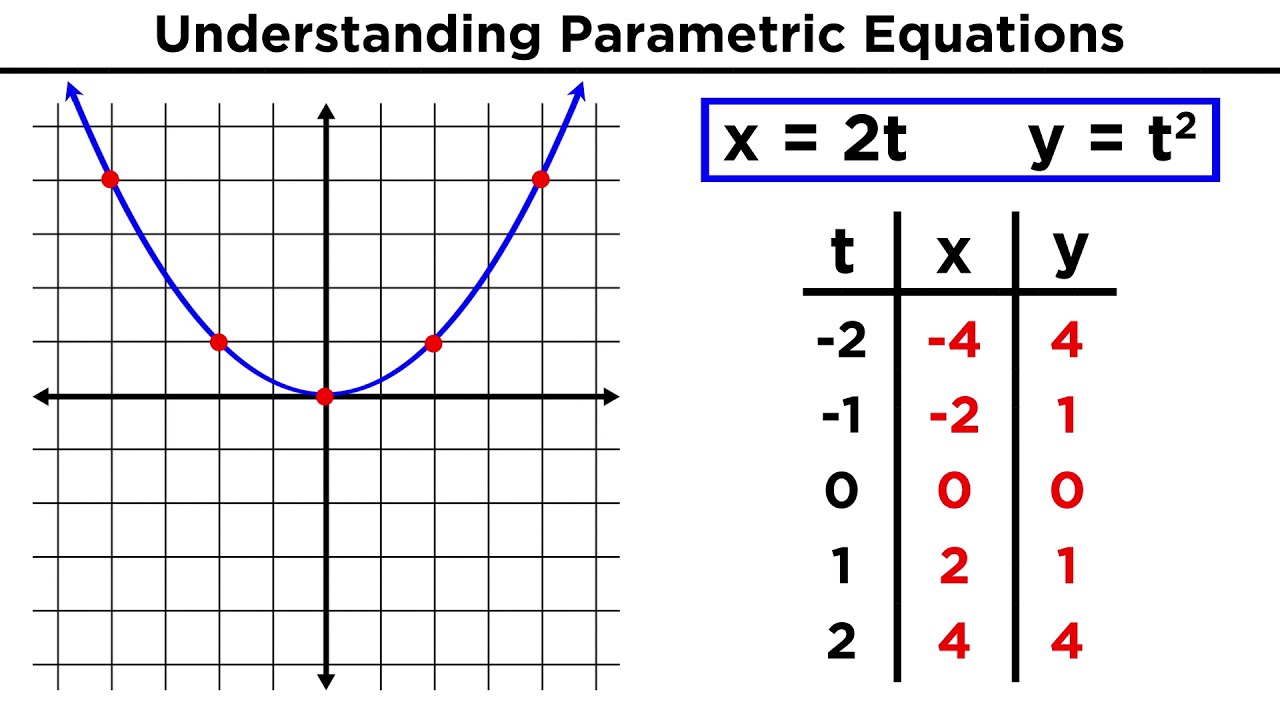
📊 The script provides a detailed example of how to graph a parametric equation by plugging in values for the parameter to find corresponding x and y coordinates, and then plotting these points to form a curve.
🔢 The process of finding the initial and terminal points is crucial for determining the curve's orientation and trajectory.
🎯 The concept of symmetry in parametric equations is introduced, noting that if a curve is symmetric about the x-axis and y-axis, it can be drawn in one quadrant and then reflected to fill the other quadrants.
🛤️ The script also discusses the concept of a curve's 'direction', which is essential for understanding the path an object takes as it moves along the curve.
📚 The importance of practice and application is emphasized, with the script encouraging the audience to work through multiple examples to solidify their understanding of parametric equations and their graphical representations.
🔍 The script concludes with an advanced example that demonstrates how to handle more complex parametric equations and how to use trigonometric identities to simplify the process of graphing.

Q & A

What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is parametric equations, their definition, and how they are used to describe the motion of an object on a plane.
Why are parametric equations useful in describing plane curves?
-Parametric equations are useful in describing plane curves because they allow for the representation of curves that may not be easily defined using traditional function forms. They also provide additional information such as the starting point, ending point, and direction of the motion of an object along the curve.
What are some of the limitations of using rectangular coordinates to define plain curves?
-Some limitations of using rectangular coordinates to define plain curves include the inability to explicitly define certain curves in terms of a single variable, the difficulty in describing non-functional curves, and the lack of information about the direction and orientation of the curve.
How do parametric equations overcome the limitations of traditional function definitions?
-Parametric equations overcome these limitations by defining both x and y as functions of a third variable, typically time (t). This approach allows for the description of the curve's motion, including its starting point, ending point, and direction, regardless of whether the curve can be defined as a traditional function.
What is the role of the parameter 't' in parametric equations?
-In parametric equations, 't' is the independent variable, also referred to as the parameter. It is used to define both x and y coordinates as functions of 't', which allows for the tracing of the path of an object moving on a plane over time.
How does the concept of a plane curve differ from that of a three-dimensional curve?
-A plane curve refers to the motion of an object on a two-dimensional plane, whereas a three-dimensional curve involves motion in three-dimensional space. A plane curve is confined to a flat surface, while a three-dimensional curve can navigate through the volume of space.
What are the benefits of using parametric equations in calculus and physics?
-Parametric equations are beneficial in calculus and physics as they provide a comprehensive way to describe the motion of objects, including complex paths that may not be describable using traditional function forms. They are particularly useful in analyzing motion, trajectories, and rates of change in various physical phenomena.
Can parametric equations represent curves that are not functions?
-Yes, parametric equations can represent curves that are not functions. This is because they define each point on the curve independently, without the need for a strict input-output relationship that defines traditional functions.
What is the significance of the initial and terminal points in parametric equations?
-The initial and terminal points in parametric equations are significant as they define the start and end of the object's motion along the curve. These points provide essential information about the trajectory and can be used to determine the overall shape and orientation of the curve.
How can you determine the direction of a curve described by parametric equations?
-The direction of a curve described by parametric equations can be determined by considering the order in which points are generated as the parameter 't' increases. By plotting points and connecting them in the sequence defined by the parameter, the direction of the curve can be inferred from the path taken by the object.

Outlines

00:00

📚 Introduction to Parametric Equations

The paragraph introduces the concept of parametric equations as an alternative way to describe the motion of an object in a plane. It explains that while traditional functions may not always be suitable to describe such motion, parametric equations offer a solution by allowing the definition of x and y coordinates as functions of a third variable, often time (t). The paragraph emphasizes the importance of understanding the start and end points of the motion, as well as the direction of travel, which are inherently captured by parametric equations.

05:01

🔍 Challenges with Defining Plain Curves

This section discusses the difficulties associated with defining plain curves using traditional rectangular coordinates. It highlights that many curves cannot be explicitly defined in terms of a single variable, and some are not functions at all. The paragraph also points out that even when a curve can be defined, it may not convey information about the starting and ending points or the direction of the motion, which are crucial for understanding the curve's trajectory.

10:02

🌟 Advantages of Parametric Equations

The paragraph explains the advantages of using parametric equations to define plane curves. It emphasizes that parametric equations allow for the inclusion of start and end points, as well as direction, which are not always possible with traditional functions. The explanation includes a discussion of how parametric equations can describe the motion of an object over time, providing a more comprehensive understanding of the curve's path.

15:09

📈 Graphing Parametric Equations

This section delves into the process of graphing parametric equations. It explains that while one can plot points by plugging in values for the parameter, it's often more efficient to first understand the curve's trajectory and then plot the points. The paragraph also introduces the concept of the parameter interval, which defines the range of the parameter and, consequently, the portion of the curve that will be graphed.

20:10

🤔 Example of Parametric Equations

The paragraph provides an example of a parametric equation and walks through the process of determining the curve it represents. It explains how by plugging in specific values for the parameter, one can find the corresponding x and y coordinates. The section also touches on the concept of the natural domain of the parameter and how to find it when no interval is given.

25:11

📊 Combining Equations and Trigonometry

This part of the script discusses the use of trigonometric identities to combine parametric equations and get a clearer picture of the curve they represent. It explains how isolating trigonometric functions and using identities can help in deriving an equation that relates x and y, making it easier to visualize the graph. The paragraph also emphasizes the importance of understanding the interval and direction of the parameter in plotting the curve accurately.

30:12

🌐 Symmetry and Graphing

The paragraph explores the concept of symmetry in parametric equations and how it can be used to reduce the amount of work needed to graph the equation. It explains that if the equation is even in terms of both x and y, then only one quadrant needs to be graphed, with the other quadrants following by symmetry. The section also discusses how to determine the direction of the curve and how to use this information to plot the curve efficiently.

Mindmap

Keywords

💡Parametric Equations

Parametric equations are a mathematical tool used to describe the motion of an object in a plane. They define both x and y coordinates as functions of a third variable, typically time (t), allowing for the representation of curves that may not be easily defined using traditional function forms. In the context of the video, parametric equations are introduced as a way to tackle the challenges associated with defining plane curves, especially when these curves are not functions or cannot be explicitly defined in terms of a single variable.

💡Plane Curves

Plane curves refer to the trajectory or path that an object follows on a two-dimensional plane. These curves can be complex and may not always lend themselves to being defined by traditional Cartesian coordinate functions (y = f(x)). The video emphasizes the challenges in defining plane curves, particularly when they are not functions or cannot be explicitly defined in one variable, and introduces parametric equations as a solution.

💡Polar Coordinates

Polar coordinates are a two-dimensional coordinate system in which each point on the plane is determined by a distance from a reference point and an angle from a reference direction. Unlike Cartesian coordinates, which use x and y values, polar coordinates use radial distance (r) and angular displacement (θ). The video mentions polar coordinates in the context of discussing parametric equations and the calculus associated with them, suggesting that they are another mathematical tool for analyzing and describing curves in a plane.

💡Numerical Integration

Numerical integration is a broad term for various algorithms that perform the numerical approximation of integrals, or the calculation of the area under a curve. In the context of the video, numerical integration is mentioned as the final section of the calculus course, implying that it is a method used to approximate the area or volume of shapes defined by parametric equations or other complex functions.

💡Independent Variable

In the context of parametric equations, the independent variable is the variable that is manipulated to find the dependent variables (in this case, x and y coordinates). Often, this is time (t), but it can be any variable that allows for the calculation of the coordinates. The independent variable is 'independent' because it does not rely on the other variables in the equation to be determined.

💡Dependent Variables

Dependent variables are those whose values are determined by the values of one or more independent variables. In the context of parametric equations, x and y are dependent variables because their values depend on the value of the independent variable (often time, t). As the independent variable changes, so do the values of the dependent variables, according to the equations provided.

💡Domain

The domain of a function refers to the set of all possible input values (typically the independent variable) for which the function is defined. In the context of parametric equations, understanding the domain is crucial for determining the range of the independent variable (like time or angle) over which the curve is defined and can be plotted.

💡Interval

In mathematics, an interval refers to a set of numbers within a certain range. For parametric equations, the interval specifies the range of the independent variable (parameter) for which the equations are valid and the curve is defined. The interval helps to determine the starting point, ending point, and the direction of the curve.

💡Direction

Direction in the context of parametric equations refers to the orientation or path that the curve takes as the independent variable changes. It is important for understanding not only where the curve starts and ends but also the trajectory it follows throughout its length.

💡Trigonometric Functions

Trigonometric functions, such as sine, cosine, and tangent, are mathematical functions that relate the angles and sides of a right triangle. In the context of the video, these functions are used within parametric equations to model periodic motion or other types of oscillating behavior on a plane.

💡Symmetry

Symmetry in mathematics refers to a property of an object or shape that allows it to be identically matched with another part of itself. In the context of the video, symmetry is a key concept that helps in understanding the behavior of certain parametric equations, as it can reduce the amount of computation needed to plot the entire curve by recognizing that parts of the curve mirror each other across axes.

Highlights

The introduction of parametric equations as an alternative way to define curves that are not easily definable as standard functions.

The explanation of plane curves as the motion of an object on a flat surface, contrasting with three-dimensional curves in space.

Discussion of the limitations of defining plain curves using rectangular coordinates, such as the inability to capture the start and end points and direction of motion.

The introduction of the concept of a parameter, typically denoted as 't', to describe the motion in both X and Y directions as a function of this independent variable.

The explanation of how parametric equations allow for the description of a curve's orientation, start and end points, and the path of motion.

The use of an example to illustrate how to plot points using parametric equations and how these points define a curve with a specific direction.

The concept of the parameter interval, which defines the range of the parameter and thus the extent of the curve.

The demonstration of how to find the initial and terminal points of a curve using parametric equations and the parameter interval.

The explanation of how the shape and direction of a curve can be inferred from the algebraic form of parametric equations.

The use of trigonometric functions in parametric equations to define curves such as circles and ellipses.

The method of isolating trigonometric functions within parametric equations to make them easier to graph and understand.

The application of trigonometric identities to simplify parametric equations and gain a clearer picture of the resulting curve.

The concept of symmetry in parametric equations, which can reduce the number of points needed to plot a curve by utilizing the properties of even functions.

The demonstration of how to use symmetry and algebraic properties to sketch the graph of a parametric equation without plotting every point.

The emphasis on the importance of understanding the behavior of a curve before plotting points, to make the process more efficient and accurate.

The conclusion that parametric equations provide a powerful tool for describing complex motions and shapes that cannot be captured by traditional function definitions.

Transcripts

Browse More Related Video

Ch. 8.4 Plane Curves and Parametric Equations

Parametric equations 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Parametric Equations

Lesson 11 - Arc Length In Parametric Equations (Calculus 2 Tutor)

Parametric equations 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Parametric Equations

Related Tags

Parametric Equations Graphing Techniques Mathematical Concepts Curve Analysis Trigonometry Direction and Motion Circles and Ellipses Symmetry in Graphs Calculus Applications Plane Geometry