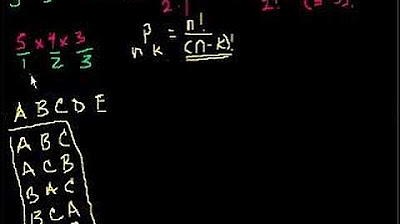Arrangements
TLDRThis educational video delves into the concept of permutations and combinations, focusing on arrangements. It demonstrates three methods to find the number of ways to arrange letters 'a', 'b', and 'c', resulting in six possible arrangements. The video further explains how to calculate arrangements for distinct items using factorials, exemplified with nine cards and specific letter arrangements. It concludes by highlighting the simplicity of understanding arrangements through these methods.
Takeaways
- 📚 The video discusses the topic of permutations and combinations, specifically focusing on arrangements.
- 🔢 The presenter demonstrates how to find the number of ways to arrange the letters A, B, and C, resulting in six possible arrangements.
- 📝 Two methods are presented for solving permutation problems: listing down arrangements and using the concept of factorial.
- 📦 A practical example is given where the presenter uses 'boxes' to represent the positions for the items to be arranged.
- ✅ The presenter confirms that the multiplication method (3 * 2 * 1) and the factorial method (3!) both yield the same result for three items.
- 📈 A general formula is provided for arranging 'n' distinct items in a line, which is n factorial (n!).
- 🃏 An example is given where the number of arrangements for nine distinct cards is calculated as nine factorial (9!).
- 📐 The presenter explains that distinct items mean no two items are the same, which is crucial for factorial calculations.
- 📝 A specific scenario is discussed where arrangements must begin with the letter 'G', resulting in 5 factorial (5!) arrangements.
- 🔍 Another scenario is presented where arrangements must begin with 'G' and end with 'S', leading to 7 factorial (7!) possible arrangements.
- 👍 The video concludes with an encouragement for viewers to like, comment, and subscribe for more educational content.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is permutations and combinations, specifically focusing on the arrangements of items.
How many different arrangements can be made with the letters A, B, and C?
-There are six different arrangements possible with the letters A, B, and C.
What are the three methods mentioned in the video to find the number of arrangements for the letters A, B, and C?
-The three methods mentioned are: 1) Listing down all possible arrangements manually, 2) Using the concept of placing items in boxes and multiplying the choices, and 3) Using the factorial of the number of items (3 factorial in this case).
What is the formula for the number of ways to arrange n distinct items in a line?
-The formula for the number of ways to arrange n distinct items in a line is n factorial (n!).
How many arrangements are possible with nine distinct cards if there are no restrictions?
-With nine distinct cards and no restrictions, there are nine factorial (9!) arrangements possible, which equals 362,880.
What is the total number of arrangements if the arrangement must begin with the letter 'G'?
-If the arrangement must begin with the letter 'G', there are five factorial (5!) arrangements possible, which equals 120.
How many different arrangements can be made if an arrangement starts with 'G' and ends with 'S'?
-If an arrangement starts with 'G' and ends with 'S', there are seven factorial (7!) arrangements possible, which equals 5,040.
What does 'distinct items' mean in the context of permutations?
-In the context of permutations, 'distinct items' means that no two items are the same; each item is unique.
What is the significance of using factorial in permutation problems?
-The significance of using factorial in permutation problems is that it accounts for the number of ways to arrange a set of items where the order matters, with each item being unique.
Can you provide an example of a different arrangement method not mentioned in the video?
-An example of a different arrangement method not mentioned in the video could be using a computer algorithm to generate all permutations, which can be more efficient for larger sets of items.
What is the purpose of the video in terms of education?
-The purpose of the video is to educate viewers on the concept of permutations and combinations, specifically how to calculate the number of possible arrangements for a given set of items.
Outlines
📚 Introduction to Permutations and Combinations
The video begins with an introduction to the topic of permutations and combinations, specifically focusing on the arrangement of items. The speaker illustrates the concept by using the example of arranging the letters 'a', 'b', and 'c'. They demonstrate three methods to find the number of possible arrangements: listing them out manually, using the 'boxes' method, and applying the factorial concept. The speaker emphasizes that for three distinct items, there are six possible arrangements, which can be calculated as 3 factorial (3!), equaling 6. The explanation is clear and provides a fundamental understanding of permutations without restrictions.
🔢 Applying Permutations to Card Arrangements and Specific Conditions
In the second paragraph, the speaker extends the concept of permutations to more complex scenarios, such as arranging nine distinct cards without restrictions, which is calculated as 9 factorial (9!), amounting to 362,880 arrangements. They also address permutations with specific starting conditions, such as arrangements that begin with the letter 'g', which would be 5 factorial (5!), equaling 120 different arrangements. Furthermore, the speaker tackles permutations with both starting and ending conditions, like those beginning with 'g' and ending with 's', calculated as 7 factorial (7!), resulting in 5,040 arrangements. This paragraph builds on the foundational knowledge from the first, applying it to more nuanced situations and demonstrating the versatility of permutation calculations.
Mindmap
Keywords
💡Permutation
💡Combination
💡Arrangements
💡Factorial
💡Distinct Items
💡Method
💡Choices
💡Restrictions
💡Cards
💡Grad
💡Letter
Highlights
Introduction to a video on the topic of permutations and combinations focusing on arrangements.
Explanation of arranging three distinct items (a, b, c) and the six possible arrangements.
Method one: Listing down all possible arrangements manually.
Method two: Using the concept of boxes to calculate arrangements without listing.
Method three: Utilizing the factorial concept to find the number of arrangements.
General formula for arranging n distinct items: n factorial.
Example calculation for arranging nine distinct cards using factorial.
Explanation of the number of arrangements when there are restrictions, such as starting with a specific letter.
Calculation of arrangements that begin with 'grad' using 5 factorial.
Method to find arrangements that start with 'g' and end with 's' using 7 factorial.
Final arrangement count for the 'g' and 's' scenario: 5,040.
Emphasis on the simplicity of understanding arrangements through factorials.
Encouragement for viewers to like, comment, and subscribe for more educational content.
The video provides three different methods to calculate permutations of items.
Illustration of the factorial concept with practical examples.
The importance of distinct items in permutation calculations.
How to calculate permutations with specific starting conditions.
How to calculate permutations with both starting and ending conditions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: