Special Right Triangles - 45 45 90 - Trigonometry & Geometry | SAT Math
TLDRThis video tutorial focuses on the 45-45-90 triangle, a key concept for solving problems on standardized tests like the SAT. It explains that in this right triangle, the two legs are equal and the hypotenuse is √2 times the length of a leg. The video demonstrates how to find missing sides using multiplication or division by √2. It also includes examples and a practice problem involving a triangle inscribed in a circle, emphasizing the importance of recognizing the 45-45-90 triangle's properties for quick and accurate calculations.
Takeaways
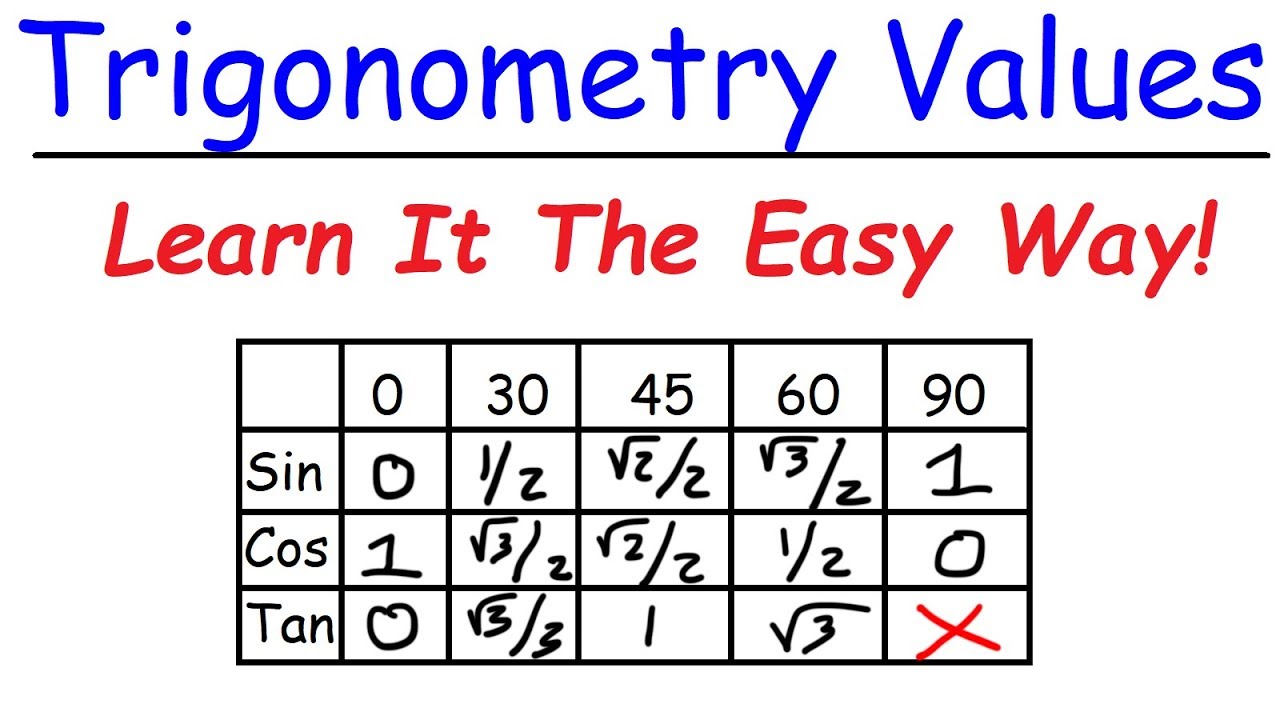
- 📐 The 45-45-90 triangle is a right triangle with two equal legs and a hypotenuse that is √2 times the length of each leg.
- 🔍 This triangle is particularly useful for solving other triangles and is beneficial for SAT or similar exams.
- 📚 To find the hypotenuse from a leg, multiply the leg's length by √2.
- 🔢 To find a leg from the hypotenuse, divide the hypotenuse's length by √2.
- 📈 The script provides examples to demonstrate the application of these rules for finding missing sides.
- 📉 When given the hypotenuse, to find the legs, rationalize the denominator by multiplying both numerator and denominator by √2.
- 📐 The script explains how to identify a 45-45-90 triangle by recognizing equal sides across the 45-degree angles.
- 📊 The area of a 45-45-90 triangle can be calculated using the formula (1/2) * base * height, where both the base and height are the legs of the triangle.
- 📘 The video includes a practice problem involving a 45-45-90 triangle inscribed in a circle, emphasizing the importance of recognizing the triangle's properties.
- 📚 The video suggests that understanding the 45-45-90 triangle can save time on exams by allowing for quick mental calculations.
- 👀 The presenter also recommends watching a follow-up video on 30-60-90 special right triangles for further exam preparation.
Q & A
What is the main focus of the video?
-The video focuses on the 45-45-90 triangle, explaining how to use it to solve other triangles, which is especially useful for SAT or the ACT exam preparation.
What are the defining characteristics of a 45-45-90 triangle?
-A 45-45-90 triangle is a right triangle with two sides of equal length, and the hypotenuse is the side opposite the right angle, which is √2 times the length of the equal sides.
How do you find the hypotenuse of a 45-45-90 triangle if you know the length of one of the legs?
-To find the hypotenuse, you multiply the length of one leg by √2.
If you know the hypotenuse of a 45-45-90 triangle, how do you find the length of one of the legs?
-To find the length of one of the legs, you divide the length of the hypotenuse by √2 and rationalize the denominator if necessary.
What is the process to find the missing sides of a 45-45-90 triangle when given one leg?
-If one leg is given, the other leg is equal to it. To find the hypotenuse, multiply the given leg's length by √2.
How does the video demonstrate the application of the 45-45-90 triangle properties?
-The video demonstrates it by providing examples where the length of one leg or the hypotenuse is given, and then showing the steps to find the missing sides.
What is the significance of the center of the circle (point B) in the practice problem presented in the video?
-In the practice problem, point B being the center of the circle ensures that AB and BC are radii of the circle and therefore must be equal, confirming the triangle is a 45-45-90 triangle.
How is the area of triangle ABC calculated in the practice problem?
-The area is calculated by taking one-half the product of the base and the height of the triangle. Since both are 8√2, the area is 1/2 × 8 × 8 × 2 = 64 square units.
Why is understanding the 45-45-90 triangle important for standardized tests like the SAT or ACT?
-Understanding the 45-45-90 triangle is important because it allows for quick mental calculations, saving time during the test, which is crucial for performance.
What advice does the video give for dealing with 45-45-90 triangles during exams?
-The video advises to remember the rule of multiplying by √2 when you have a leg and need the hypotenuse, and dividing by √2 when you have the hypotenuse and need a leg, to quickly find the missing sides.
Outlines
📚 Introduction to 45-45-90 Triangles
This paragraph introduces the concept of the 45-45-90 triangle, emphasizing its importance in solving other triangle problems, particularly for standardized tests like the SAT or the ACT. The 45-45-90 triangle is a right triangle with two equal sides, and the hypotenuse is \( \sqrt{2} \) times the length of one of the equal sides. The paragraph explains how to find missing sides by either multiplying by \( \sqrt{2} \) or dividing by \( \sqrt{2} \), depending on which side is known. Examples are provided to illustrate the application of these rules.
📐 Solving 45-45-90 Triangles with Given Sides
The second paragraph continues the discussion on 45-45-90 triangles, providing step-by-step instructions on how to solve for missing sides when different sides are known. It includes examples where the leg or the hypotenuse is given, and demonstrates the process of finding the remaining sides using multiplication or division by \( \sqrt{2} \). The paragraph also includes a practice problem involving a triangle inscribed in a circle, which reinforces the understanding of the properties of 45-45-90 triangles and their application in geometry.
🔍 Applying 45-45-90 Triangles to a Circle Problem
In the final paragraph, the script presents a practice problem involving a triangle ABC with a hypotenuse of 16 units and a center B at the center of a circle. The paragraph explains how to determine that triangle ABC is a 45-45-90 triangle based on the properties of the circle and the equal radii. It then guides the viewer through the process of finding the lengths of the other two sides by dividing the hypotenuse by \( \sqrt{2} \) and rationalizing the denominator. Finally, it calculates the area of the triangle using the base and height, resulting in an area of 64 square units.
Mindmap
Keywords
💡45-45-90 Triangle
💡Hypotenuse
💡Legs
💡Square Root of 2
💡Rationalize the Denominator
💡Isosceles Right Triangle
💡SAT Exam
💡HT Exam
💡Special Reference Triangle
💡Area of a Triangle
💡Practice Problem
Highlights
The video focuses on the 45-45-90 triangle, a crucial concept for solving other triangles and preparing for exams like the SAT.
A 45-45-90 triangle is a right triangle with two equal sides, and the hypotenuse is √2 times the length of each leg.
To find the hypotenuse given a leg of a 45-45-90 triangle, multiply the leg's length by √2.
To find a leg given the hypotenuse, divide the hypotenuse's length by √2.
An example is provided to illustrate finding the missing sides of a 45-45-90 triangle with a given leg length.
Another example demonstrates calculating the hypotenuse and legs when given different side lengths.
The video explains how to find the hypotenuse when given one leg of a 45-45-90 triangle.
The method for finding the missing sides when given the hypotenuse is demonstrated with additional examples.
A practice problem involving a 45-45-90 triangle inscribed in a circle is presented.
The importance of recognizing the 45-45-90 triangle's properties when the triangle is inscribed in a circle is highlighted.
The calculation of the area of a 45-45-90 triangle is shown using the base and height.
The area of triangle ABC is found to be 64 square units, providing a clear example of applying the 45-45-90 triangle properties.
The video concludes with a tip on how to quickly find missing sides in a 45-45-90 triangle during exams.
A teaser for the next video on 30-60-90 special right triangles is given, indicating a series of educational content.
The video emphasizes the efficiency of using the 45-45-90 triangle properties for quick calculations on exams.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: