Vectors Physics Class 11th
TLDRThis engaging video script dives into the fundamental concept of vectors, a topic often considered complex but here simplified for better understanding. The video begins by differentiating between scalars, which have only magnitude, and vectors, which possess both magnitude and direction. It uses examples such as mass, distance, and temperature to illustrate scalars, while displacement, velocity, and force exemplify vectors. The script then introduces vector notation, explaining how vectors are represented with an arrow or in bold to denote direction. The video continues to explore various types of vectors, including position and displacement vectors, as well as polar and axial vectors. It also covers essential vector algebra terms like equal vectors, negative vectors, modulus, unit vectors, and the unique properties of the zero vector. The educational content is complemented by an invitation to engage with Manoa Academy for further learning in science, maths, coding, and artificial intelligence.
Takeaways
- 📐 **Scalars vs. Vectors**: Scalars have only magnitude (e.g., mass, distance), while vectors have both magnitude and direction (e.g., force, velocity).
- 🔍 **Vector Notation**: Vectors are denoted with an arrow (e.g., \( \vec{F} \)) or in bold (e.g., **F**), and their magnitude can be represented by a double vertical line (e.g., \( \| F \| \)) or simply the value without notation (e.g., \( F = 10 \) N).
- 📍 **Direction Significance**: The direction of a vector is crucial; for instance, force has a direction even when not explicitly stated.
- ⚖️ **Vector Addition**: Unlike scalars, vector addition follows special rules and requires consideration of direction, not just magnitude.
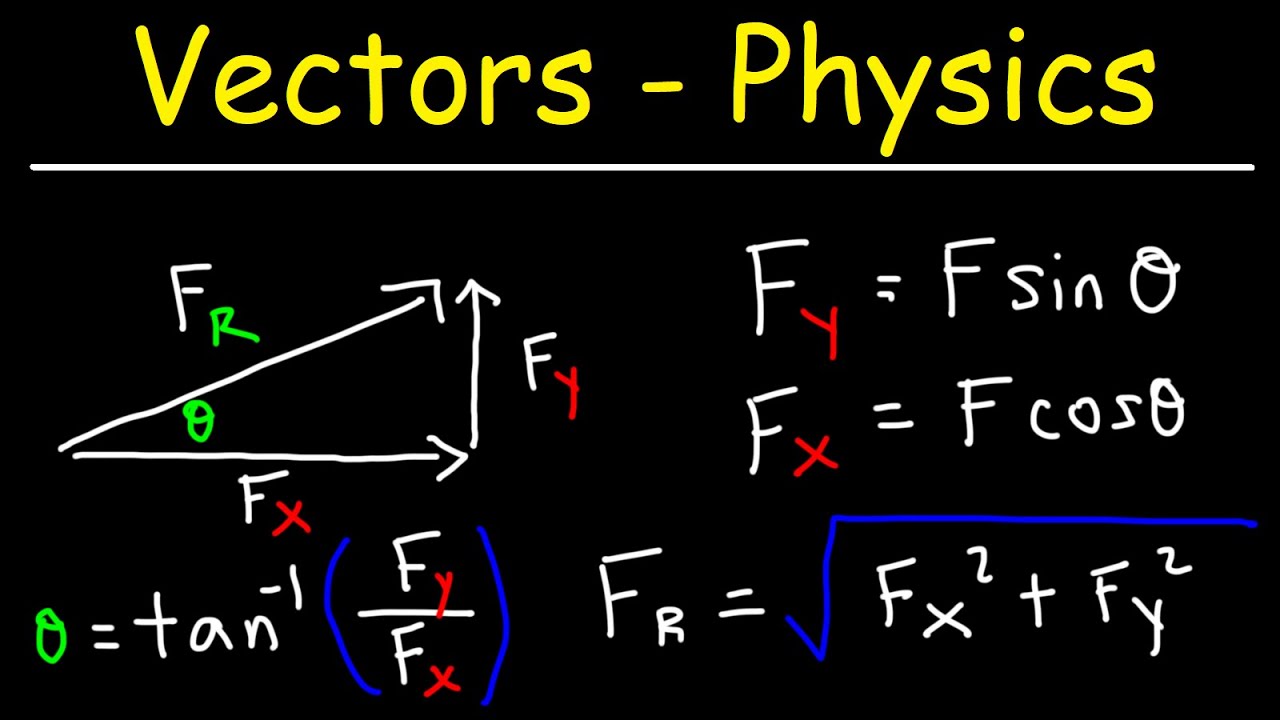
- 📈 **Visual Representation**: Vectors can be visually represented by an arrowed line, where the length indicates magnitude and the arrow shows direction.
- 📏 **Scale and Magnitude**: In diagrams, a scale is used to represent vector magnitudes, such as 1 cm representing 2 Newtons.
- 📍 **Vector Terminology**: Vectors have a 'tail' at the starting point and a 'head' at the endpoint, which are important for understanding vector operations.
- 🏠 **Position Vectors**: Describe the position of an object in space relative to an origin, using both magnitude and direction.
- 🔄 **Displacement Vectors**: Represent the change in position from one point to another, ignoring the path taken and only considering the initial and final positions.
- 🌀 **Polar and Axial Vectors**: Polar vectors have a point of application (e.g., displacement, velocity), while axial vectors represent rotational effects along an axis (e.g., angular velocity, torque).
- 🔢 **Vector Algebra**: Terms like equal vectors, negative vectors, modulus, unit vectors, fixed vectors, free vectors, collinear vectors, co-planar vectors, co-initial vectors, co-terminus vectors, and the zero vector are fundamental to vector algebra.
- 🧮 **Zero Vector Properties**: The zero vector, denoted as \( \vec{0} \), has a magnitude of zero and an arbitrary direction, acting as the additive identity in vector operations.
- 🤝 **Scalar Multiplication**: Multiplying a vector by a real number (scalar) results in a new vector with a scaled magnitude and the same or opposite direction, depending on the sign of the scalar.
Q & A
What is the fundamental difference between scalar and vector quantities?
-Scalar quantities have only magnitude without direction, such as mass, distance, time, and temperature. Vector quantities, on the other hand, have both magnitude and direction, like displacement, velocity, force, and momentum.
How can you represent a vector quantity mathematically?
-Vector quantities can be represented with an arrow above the letter (e.g., \( \vec{F} \)) or in bold (e.g., **F**) to indicate they have direction. For example, a force vector can be written as \( \vec{F} = 10 \, \text{N} \, \text{East} \).
What does the term 'modulus' refer to in the context of vectors?
-The modulus of a vector refers to its magnitude or length, which can be represented by drawing two vertical lines around the letter (e.g., \( \| F \| \)) or without vector notation (e.g., \( F = 10 \, \text{N} \)).
How can you visually represent a vector?
-Vectors can be visually represented by drawing a straight line with an arrowhead at one end. The length of the line indicates the magnitude of the vector, and the arrowhead indicates the direction.
What is a position vector and how is it used?
-A position vector describes the location or position of a point or object in space relative to a chosen reference point or origin. It is represented from the origin to the point's location and has both magnitude and direction.
How do you calculate the magnitude of a position vector?
-The magnitude of a position vector can be calculated using the Pythagorean theorem, which is applicable since the vector components form a right-angled triangle.
What is a displacement vector and how is it different from a position vector?
-A displacement vector represents the change in position of an object as it moves from one point to another. Unlike position vectors that describe an object's location, displacement vectors describe the shortest distance and direction from the initial to the final position, regardless of the path taken.
What are the two broad categories of vectors?
-Vectors can be categorized into polar vectors, which have a starting point or point of application, and axial vectors, which represent a rotational effect and act along the axis of rotation.
What is a unit vector and how is it related to a given vector?
-A unit vector is a vector with a magnitude of one, drawn in the direction of the given vector. Any vector can be expressed as its magnitude times its unit vector (e.g., \( \vec{a} = |\vec{a}| \hat{\vec{a}} \), where \( \hat{\vec{a}} \) is the unit vector).
What is a zero vector and what are its properties?
-A zero vector, also known as a null vector, has a magnitude of zero and no specific direction. It acts as the additive identity for vectors, meaning that adding a zero vector to any vector results in the original vector.
How does scalar multiplication affect a vector?
-Scalar multiplication involves multiplying a vector by a real number, which results in a new vector that is related to the original vector by scaling its magnitude. If the scalar is positive, the direction remains the same; if negative, the direction is opposite.
What are colinear and co-planar vectors?
-Colinear vectors are those that act along the same line or parallel lines. Co-planar vectors lie in the same plane. If two vectors are colinear and have the same direction, they are also called parallel vectors.
Outlines
🧭 Understanding Vectors: Basics and Notation
This section introduces the fundamental concept of vectors, emphasizing their difference from scalars, which only have magnitude without direction. Vectors, which possess both magnitude and direction, are illustrated with examples like displacement and force. The video also explains the special notation used for vectors, such as using arrows or bold to denote vector quantities, and the importance of vector addition. This introduction sets the stage for understanding more complex vector operations by establishing the basic language and graphical representations of vectors.
🔄 Advanced Vector Concepts: Types and Operations
This part delves into specialized types of vectors such as position and displacement vectors, explaining their application in physics to denote movement and location in space relative to a reference point. It also covers polar and axial vectors, differentiating them based on their physical implications in rotational movements. The usage of vectors in mathematical operations like vector subtraction and addition is discussed, providing examples to illustrate how vectors interact differently than scalars when combined.
📏 Vector Relationships and Special Cases
The discussion continues with an exploration of vector relationships, including equal, negative, and co-linear vectors. It introduces various vector terms such as co-initial and co-terminus vectors, explaining their significance in geometric and physical contexts. Special types of vectors like zero vectors, which act as the additive identity in vector algebra, are highlighted to show their role in simplifying mathematical expressions involving vectors. This segment helps viewers understand the depth of vector interactions and their mathematical properties.
🧑🏫 Practical Applications of Vectors and Mathematical Properties
This section covers the practical implications and mathematical operations involving vectors, such as scalar multiplication, which affects the magnitude and direction of vectors. It discusses the zero vector in detail, emphasizing its importance in theoretical and practical scenarios. Additionally, the relationship between vectors and scalars through operations like scalar multiplication is explored, illustrating how these interactions modify vector properties and their impact on vector analysis.
🔢 Scalar Multiplication and Conclusion on Vectors
The final part synthesizes the entire discussion on vectors, focusing on scalar multiplication and its effects on vector magnitude and direction. It serves as a conclusion to the vector series, encouraging viewers to apply their understanding to solve problems and visualize vector interactions. The call to action invites viewers to engage further with the channel's educational content, reinforcing the application-oriented approach of the video series on vectors.
Mindmap
Keywords
💡Vectors
💡Scalar Quantities
💡Vector Notation
💡Magnitude
💡Direction
💡Vector Addition
💡Position Vector
💡Displacement Vector
💡Polar and Axial Vectors
💡Unit Vector
💡Zero Vector
Highlights
Vectors are physical quantities that have both magnitude and direction, unlike scalars which only have magnitude.
Scalar quantities include mass, distance, time, and temperature, which lack direction.
Examples of vector quantities include displacement, velocity, force, and momentum.
Vector addition cannot be performed using simple algebraic laws; it requires special vector addition laws.
Vector notation is represented by an arrow over the letter or bold formatting to indicate direction.
The magnitude of a vector can be represented by a straight line with an arrowhead, where the length indicates magnitude and the arrowhead indicates direction.
A position vector describes the location of a point or object in space relative to an origin, using both magnitude and direction.
Displacement vectors represent the change in position from an initial to a final point, disregarding the path taken.
Polar vectors have a starting point or point of application, such as displacement and velocity vectors.
Axial vectors represent a rotational effect and act along the axis of rotation, like angular velocity and torque.
Equal vectors have the same magnitude and direction.
The negative of a vector has the same magnitude but the opposite direction.
The modulus of a vector, or its magnitude, is a scalar quantity representing the vector's length without direction.
Unit vectors have a magnitude of one and are used to specify the direction of a vector.
Fixed vectors have a fixed initial point, such as the position vector of a particle at the origin.
Free vectors do not have a fixed initial point and can be applied at any point, like force vectors.
Collinear vectors act along the same line or parallel lines, and parallel vectors have the same direction.
Anti-parallel vectors are collinear vectors with opposite directions, forming a 180° angle.
Co-planar vectors lie in the same plane, whereas a vector not in the same plane as others is not co-planar.
Co-initial vectors share the same starting point, and co-terminus vectors share a common ending point.
The zero vector, denoted with an arrow or zero, has a magnitude of zero and an arbitrary direction, serving as the additive identity for vectors.
Scalar multiplication of a vector by a real number results in a new vector with scaled magnitude and the same or opposite direction depending on the sign of the scalar.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: