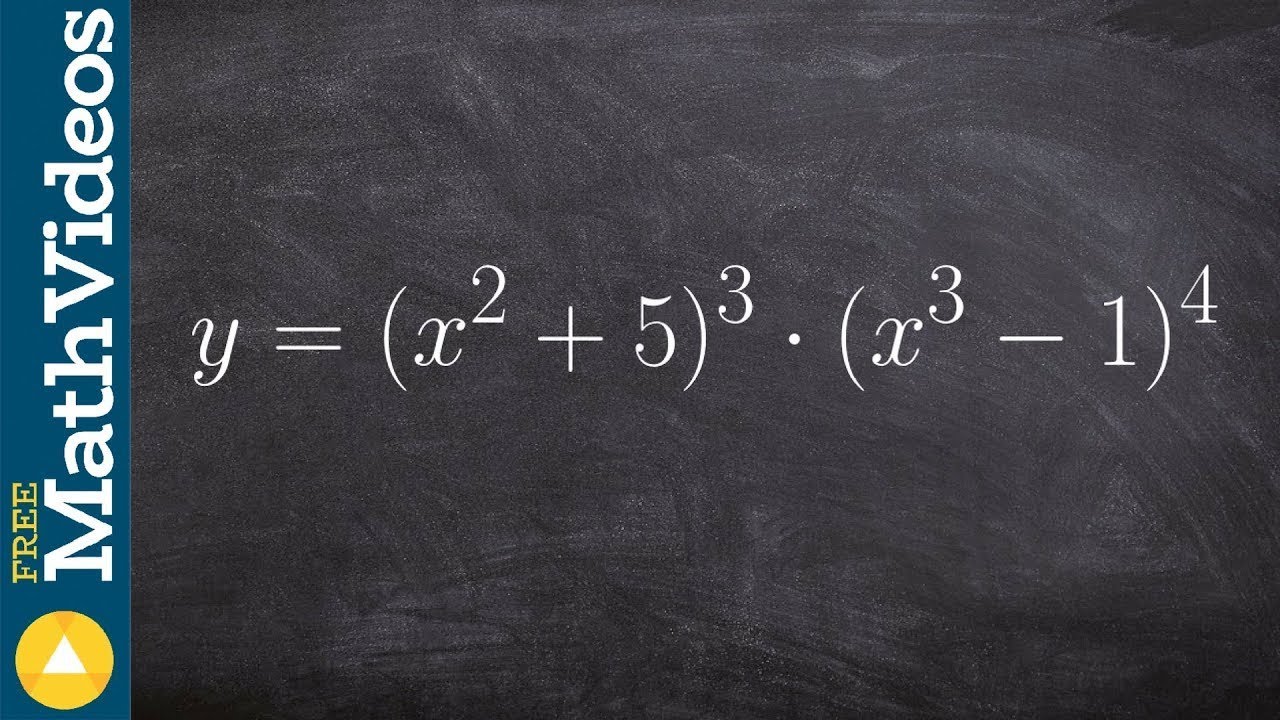More Chain Rule (NancyPi)
TLDRIn this educational video, Nancy dives into the intricacies of calculus, specifically focusing on the application of the chain rule and its combination with the product rule. She begins by addressing a common oversight in her previous video, where she had presented problems but not explained them. Nancy rectifies this by illustrating how to use the chain rule to find derivatives of functions in exponential form, such as natural logarithms and square roots. She emphasizes the importance of differentiating the outer function first, leaving the inner function untouched, and then multiplying by the derivative of the inner function. The video also clarifies the order of operations when dealing with both the chain and product rules, demonstrating that the product rule is typically applied first when the function is viewed as a product of two parts. Nancy provides step-by-step examples, including simplifying the expressions and converting between power and root forms for clarity. She encourages viewers to check out her introductory chain rule video for a more comprehensive understanding and ends with a light-hearted invitation to like or subscribe for more content.
Takeaways
- 📚 First, understand the basics of the chain rule by watching the introductory video if you're new to the concept.
- 🔑 When applying the chain rule, start by taking the derivative of the outer function and keep the inner function unchanged.
- 📈 For the exponential function e^x, its derivative is e^x itself, and then multiply by the derivative of the inner function.
- 🌟 The derivative of a natural logarithm ln(x) is 1/x, but with the chain rule for ln(5x), it becomes 1/(5x) * 5, simplifying to 1/x.
- 🆗 Always remember to multiply by the derivative of the inner function after taking the derivative of the outer function.
- 🛠 When dealing with roots or fractional powers, rewrite them as a power to make application of the power rule easier.
- 🤔 For expressions involving both the chain rule and the product rule, first identify the outermost function to determine the order of operations.
- 🔍 In the product rule, the derivative of a product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first.
- 📝 When simplifying derivatives, look for common factors and coefficients that can be cleanly extracted to simplify the final expression.
- 🏎 In complex derivatives involving multiple rules, perform operations step by step, starting with the outermost function application.
- 👍 Engage with the content by liking or subscribing if the explanation was helpful, to support further educational content creation.
Q & A
What is the first step in applying the chain rule to find the derivative of a function?
-The first step in applying the chain rule is to take the derivative of the outside function and keep the inside function unchanged.
How do you handle the inside function when applying the chain rule?
-When applying the chain rule, you leave the inside function alone initially, then multiply the derivative of the outside function by the derivative of the inside function.
What is the derivative of the exponential function e raised to a power?
-The derivative of the exponential function e raised to a power is the same exponential function itself.
What is the proper form for writing the derivative of a function using the chain rule?
-The proper form is to bring any coefficients in front of the exponential or logarithmic function and to simplify the expression as much as possible.
Can you apply the chain rule to a natural log function with a variable inside?
-Yes, you can apply the chain rule to a natural log function with a variable inside by taking the derivative of the natural log and then multiplying by the derivative of the variable inside.
What happens when you apply the chain rule to ln(5x)?
-When applying the chain rule to ln(5x), you get (1/5x) multiplied by the derivative of 5x, which is 5, resulting in a simplified derivative of 1/x.
What is the process for finding the derivative of a square root function using the chain rule?
-First, rewrite the square root as a power to the one-half, then apply the power rule to the outside function, and finally multiply by the derivative of the inside function.
When do you use the Product Rule in conjunction with the chain rule?
-You use the Product Rule first when you have a product of two functions and then apply the chain rule to each function if necessary, as dictated by the outermost form of the expression.
How do you determine the order of operations when you have both the Product Rule and the Chain Rule to apply?
-You first address the outermost form of the expression. If it's a product, use the Product Rule first, and if it's a composition, use the Chain Rule first.
What does the Product Rule state in terms of finding the derivative of a product of two functions?
-The Product Rule states that the derivative of a product of two functions is the first function times the derivative of the second function plus the second function times the derivative of the first function.
How can you simplify the derivative you found using the Product Rule and the Chain Rule?
-You can simplify by cleaning up coefficients, combining like terms, and factoring out common terms to get a neater expression.
What is the significance of understanding the order of operations in calculus, such as when to use the Product Rule before the Chain Rule?
-Understanding the order of operations ensures that you correctly apply mathematical rules to find the derivative of complex functions, which is crucial for accurate mathematical analysis and problem-solving.
Outlines
📚 Introduction to the Chain Rule
Nancy begins by addressing her previous video, where she left viewers with unresolved problems. She acknowledges the request from her audience to explain the application of the chain rule, particularly for functions in exponential form, such as natural logarithms and square roots, and in conjunction with the product rule. Nancy provides a reminder of the chain rule's basic steps: first, differentiate the outer function and leave the inner function untouched, then multiply by the derivative of the inner function. She uses the example of \( e^{3x} \) to illustrate the process, leading to the derivative \( 3e^{3x} \). Nancy also suggests checking out her introductory chain rule video for a more comprehensive understanding and reassures viewers that she will clarify the order of operations between the chain rule and the product rule.
🔍 Applying the Chain Rule to Different Functions
The second paragraph delves into applying the chain rule to various types of functions, starting with a natural logarithm example, \( \ln(5x) \). Nancy demonstrates the steps of differentiating the outer function, using \( 1/5x \) as the derivative of \( \ln(5x) \), and then multiplying by the derivative of the inner function, which is 5. The result simplifies to \( 1/x \), which is a surprising outcome that serves as a useful mnemonic. She then moves on to a square root function, \( \sqrt{x^2 + 1} \), and explains the process of rewriting the square root as a power to facilitate differentiation. The derivative is found using the power rule and the chain rule, resulting in \( (2x + 1)/\sqrt{x^2 + 1} \). Nancy also discusses the combined use of the chain rule and the product rule, emphasizing that the product rule is applied first when the function is viewed as a product of two functions, as seen in the example \( x^3(2x - 5)^4 \). She illustrates the process of differentiating each part separately and then combining the results according to the product rule.
🧮 Simplifying and Cleaning Up the Derivatives
In the final paragraph, Nancy focuses on the process of simplifying the derivatives obtained from the chain rule and the product rule. She emphasizes the importance of cleaning up coefficients and extracting common factors to present the final answer in a neater form. Using the previous example, she shows how to factor out \( x^2 \) and \( (2x - 5)^3 \) from the derivative terms, resulting in a simplified expression. Nancy acknowledges that while this may seem like tedious work, it leads to a more elegant final result. She also addresses the question of which rule to apply first when faced with a combination of the chain rule and the product rule, explaining that it depends on the outermost function. She concludes by encouraging viewers to like and subscribe if they found the video helpful, highlighting the universal struggle with calculus and the goal of making it more accessible.
Mindmap
Keywords
💡Chain Rule
💡Exponential Function
💡Natural Logarithm
💡Product Rule
💡Derivative
💡Square Root
💡Power Rule
💡Coefficient
💡Lagrange Notation
💡Composite Function
💡Simplifying
Highlights
Nancy explains the use of the chain rule to find the derivative of exponential and logarithmic functions.
The chain rule is also applicable when combining it with the Product Rule, which can be confusing.
Derivative of an exponential function e^(3x) involves taking the derivative of the outside function and multiplying by the derivative of the inside function.
For the natural log function, the derivative is found by taking the derivative of the outside function and multiplying by the derivative of the inside function, which simplifies to 1/x for ln(5x).
When dealing with a square root as an outer function, it's easier to rewrite it as a fraction power before taking the derivative.
The Power Rule is used to find the derivative of the outer function in a composite function, reducing the power by one.
The Product Rule is applied when the largest view of the function shows a product of two functions.
The Product Rule states that the derivative of a product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first.
When combining the chain rule with the Product Rule, you first use the rule that applies to the outermost form of the function.
The chain rule can be used within the Product Rule when dealing with a composite function that includes a power.
Simplifying the derivative by cleaning up coefficients and pulling out common factors is considered proper and often necessary.
The order of applying the chain rule and Product Rule depends on the structure of the function, with the outermost form dictating the first rule to apply.
Nancy provides a detailed example of using the chain rule within the Product Rule, resulting in a simplified expression.
The chain rule can be used first on an outer function like a natural log if the inner function is a product.
Calculus may not be everyone's favorite subject, but understanding the chain rule can be made easier through clear explanations and examples.
Nancy encourages viewers to like and subscribe for more educational content on calculus and other mathematical topics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: