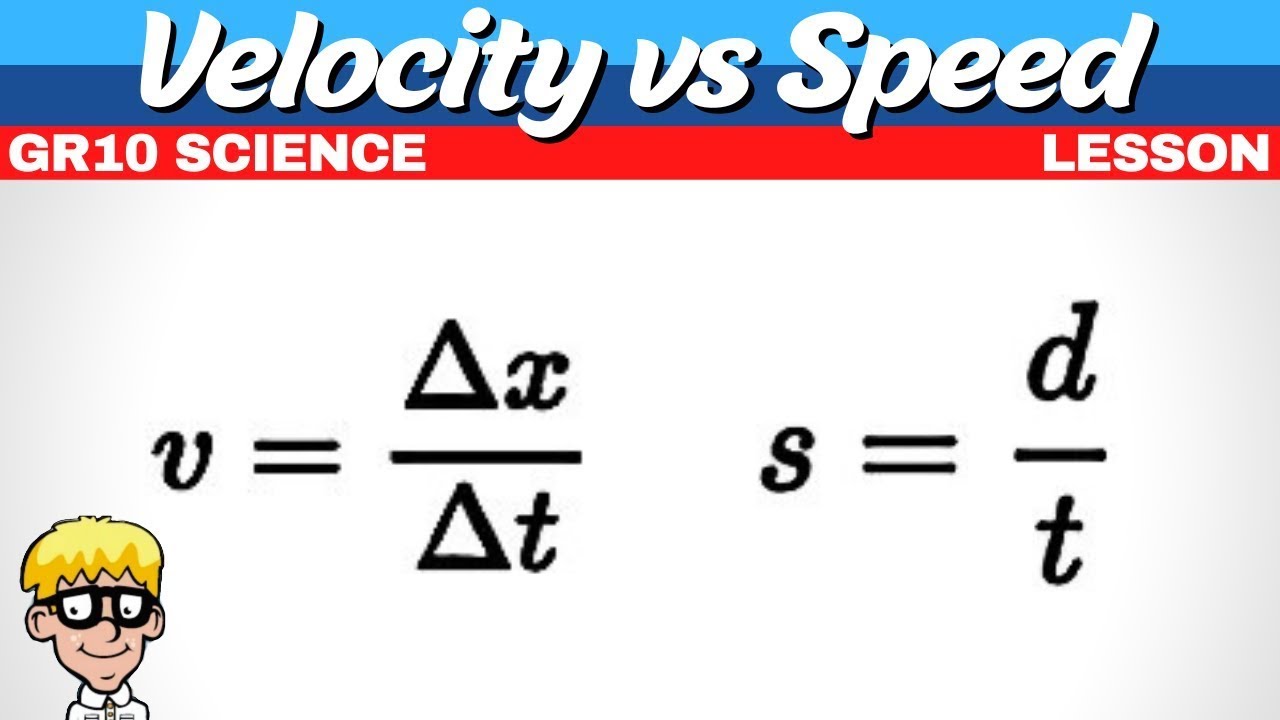Uniform Motion and Non-uniform Motion | Physics | Don't Memorise
TLDRThe video script discusses the concept of uniform motion, where an object, such as a man training for a marathon, maintains a constant speed. It explains that with uniform motion, the total distance covered can be calculated by multiplying the constant speed by the time duration, using the SI unit of speed, meters per second. The script also contrasts this with non-uniform motion, where the speed varies, and introduces the concept of average speed, which is the total distance divided by the total time taken. It provides an example of calculating average speed and emphasizes the importance of using standard units to avoid mistakes. The script concludes by mentioning instantaneous speed, which is the speed at a particular moment in time, especially relevant in scenarios with varying speeds like traffic.
Takeaways
- 🏃 The man in the script is training for a marathon by running at a constant speed of 3 meters per second, which is an example of uniform motion.
- ⏱️ Uniform motion allows for the calculation of total distance covered by multiplying the constant speed by the total time of motion.
- 📏 In the case of the marathon runner, running for a minute at 3 meters per second would result in a distance of 180 meters covered.
- 🔢 The SI unit for speed is meters per second, but other units like centimeters per second, miles per hour, and kilometers per hour are also used.
- 🚴 In everyday life, it's rare to encounter uniform motion; most motion is non-uniform due to external factors like traffic and varying energy levels.
- 🚦 Non-uniform motion is characterized by varying speeds at different points in time, and its rate is described by average speed.
- 📐 To calculate average speed, divide the total distance covered by the time taken, ensuring units are consistent and standardized.
- 🕒 For example, if someone walks 60 meters in 60 seconds, their average speed is 1 meter per second.
- ⚖️ It's crucial to maintain consistency in units when calculating speed to avoid errors, such as incorrectly interpreting one minute as one second.
- 🕰️ Average speed is useful for estimating travel times in situations with varying speeds, like driving in traffic.
- 📈 Instantaneous speed refers to the speed of an object at a particular moment in time, as opposed to the average speed over a period.
Q & A
What is the man in the script training for?
-The man in the script is training to run a marathon.
What is the distance covered by the man every second during his training?
-The man covers a distance of 3 meters every second during his training.
What is the term used to describe the man's running pace in the script?
-The term used to describe the man's running pace is uniform motion.
If the man runs at a uniform speed of 3 meters per second for a minute, how much distance does he cover?
-If the man runs at a uniform speed of 3 meters per second for a minute (60 seconds), he covers a distance of 180 meters.
What is the SI unit of speed?
-The SI unit of speed is meters per second.
What are some other units in which speed can be denoted?
-Speed can also be denoted in centimeters per second, miles per hour, or kilometers per hour.
Why is it rare to see uniform motion in everyday life?
-It is rare to see uniform motion in everyday life because external factors such as traffic, traffic lights, and crowded areas often cause variations in speed.
What is the term used to describe the rate of motion when an object's speed is not constant?
-When an object's speed is not constant, the rate of motion is referred to as average speed.
How can we calculate the average speed for non-uniform motion?
-To calculate the average speed for non-uniform motion, you take the total distance covered and divide it by the total time taken.
If a boy walks 60 meters in 60 seconds, what is his average speed?
-If a boy walks 60 meters in 60 seconds, his average speed is 1 meter per second.
What is the term for the speed at each instant during non-uniform motion?
-The speed at each instant during non-uniform motion is called instantaneous speed.
Why is it important to stick to standard units when calculating speed?
-It is important to stick to standard units when calculating speed to ensure accuracy and to avoid confusion or errors in calculations.
Outlines
🏃 Understanding Uniform Motion and Speed
This paragraph explains the concept of uniform motion, where an object covers a constant distance in each equal time interval. The man in the example runs at a constant speed of 3 meters per second, allowing us to calculate the total distance covered by multiplying the speed by the time duration. The importance of using standard units like meters per second for speed is emphasized. The paragraph also contrasts uniform motion with non-uniform motion, where speed varies and average speed is used instead. The formula for calculating average speed is presented, and the need to be careful with units and convert them to standard units is highlighted.
🚗 Instantaneous Speed in Non-Uniform Motion
This paragraph delves into non-uniform motion, where the speed of an object changes at different points in time. It introduces the concept of instantaneous speed, which is the speed of an object at a particular instant. The example of driving illustrates how speed can vary from moment to moment, even dropping to 0 when stuck in traffic. The paragraph emphasizes the importance of understanding instantaneous speed to accurately describe the motion of an object at different points in time.
Mindmap
Keywords
💡Uniform motion
💡Speed
💡Distance
💡Time duration
💡Meters per second
💡Non-uniform motion
💡Average speed
💡Instantaneous speed
💡Centimeters per second
💡Miles per hour
💡Kilometers per hour
Highlights
A man is training to run a marathon, covering a constant distance of 3 meters every second, demonstrating uniform motion.
Uniform motion is characterized by a constant speed over time, allowing for the calculation of total distance covered.
The man's running speed is 3 meters per second for a minute, resulting in a total distance of 180 meters.
Speed is defined as the distance traveled per unit of time, with the SI unit being meters per second.
Speed can also be expressed in other units such as centimeters per second, miles per hour, or kilometers per hour.
In everyday life, it's rare to observe uniform motion due to external factors like traffic and varying energy levels.
Non-uniform motion occurs when the speed of an object changes over time, requiring the calculation of average speed.
Average speed is derived by dividing the total distance covered by the total time taken.
A boy walking non-uniformly from point A to point B, 60 meters away, takes 60 seconds, resulting in an average speed of 1 meter per second.
It's important to use standard units when calculating speed to avoid errors and confusion.
To convert non-standard units to meters per second, one must adjust for the time unit, such as converting minutes to seconds.
Average speed is useful for estimating travel times in varying traffic conditions.
Instantaneous speed refers to the speed of an object at a specific moment in time, as opposed to the average speed over a period.
Maintaining a consistent understanding of units and calculations is crucial for accurate speed measurements.
The concept of uniform and non-uniform motion is fundamental to understanding the principles of physics related to motion.
Real-world applications of speed calculations include professional athletics and everyday activities like commuting.
Understanding the difference between average and instantaneous speed is key to accurately describing motion.
The transcript provides a clear explanation of how to calculate and understand speed in both uniform and non-uniform motion scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: