What IS Angular Momentum?
TLDRThe video script delves into the fascinating concept of angular momentum, a fundamental principle in physics that describes the rotational motion of objects. It explains how angular momentum is calculated by multiplying an object's speed along a circular path, the circle's radius, and the object's mass. The script uses the example of a bicycle wheel to illustrate this concept and then scales up to the Earth's orbit around the Sun, highlighting the conservation of angular momentum even when the object's path changes drastically, such as if the Sun were to disappear. This conservation is a testament to the robustness of physical laws, which remain consistent even under extreme hypothetical scenarios.
Takeaways
- 🌌 **Physics Fundamentals**: Physics describes the motion of objects in the universe, including those that appear to move without going anywhere.
- 🌀 **Types of Movement**: Objects can exhibit various forms of circular motion such as spinning, revolving, rotating, and orbiting.
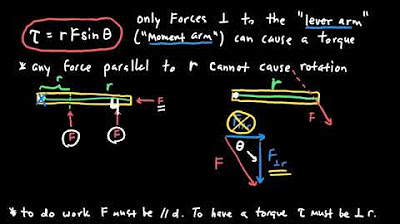
- 🚴 **Angular Momentum Definition**: Angular momentum quantifies the 'oomph' of an object moving in a circular path.
- ⚙️ **Calculating Angular Momentum**: It is calculated by multiplying the object's speed along the circle, the radius of the circle, and the object's mass.
- 🔵 **Conservation of Angular Momentum**: The total angular momentum of a system remains constant over time unless acted upon by external forces.
- 🌍 **Earth's Angular Momentum**: Earth's orbit around the sun has a specific angular momentum that remains constant year after year.
- ✨ **Continuity in Absence of Gravity**: If the sun were to disappear, Earth would still maintain its angular momentum around the point where the sun was.
- 🛑 **Straight-Line Motion**: Without the sun's gravity, Earth would move in a straight line, but the calculation of angular momentum would still yield the same value due to conservation.
- 🔢 **Magnitude of Earth's Angular Momentum**: Earth's angular momentum is vast, equating to the combined angular momentum of thousands of quintillion bicycle wheels.
- ⭕ **Imaginary Circle Concept**: In the absence of a central body, an imaginary circle's size increases as the object moves farther away, maintaining the conservation of angular momentum.
- 🔄 **Velocity and Radius Relationship**: A decrease in velocity along the circle compensates for the increase in the imaginary circle's size, keeping the angular momentum constant.
Q & A
What is the fundamental description of physics?
-Physics, at its most basic, describes the motion of objects in our universe.
What is a peculiar characteristic of some objects' motion?
-Some objects move without going anywhere, such as spinning, revolving, or rotating.
What is an example of an object that moves without going anywhere?
-A planet orbiting a star, an electron in an atom, or our solar system revolving around the gravitational center of the Milky Way.
What is the term for the quantity that describes how much force an object has when it moves in a straight line?
-The term is 'momentum'.
How is angular momentum defined?
-Angular momentum is a measure of the oomph an object has when it is moving in a circular path, and it is calculated by multiplying the object's speed along the circle, the size of the circle, and the object's mass.
What is the angular momentum of a 2 kilogram bicycle wheel with a 60 cm diameter moving at 20 km per hour?
-The angular momentum is about 7 kilogram meters squared per second.
Why is angular momentum important in the context of objects interacting through electromagnetic or gravitational forces?
-The total angular momentum of a system remains constant over time unless an external force is applied, making it a conserved quantity.
What is the angular momentum of Earth in its orbit around the Sun?
-Earth's angular momentum is 2.7 * 10^40 kilogram meters squared per second.
If the Sun were to suddenly disappear, would Earth's angular momentum remain the same?
-Yes, Earth would still have the same angular momentum about the point where the Sun was, as the decrease in velocity would cancel out the increase in the size of the imaginary circle.
What does the conservation of angular momentum imply about the laws of physics?
-The conservation of angular momentum demonstrates the robustness and universality of physical laws, as they continue to hold true even in extreme hypothetical scenarios.
What would happen to Earth's motion if the Sun and the rest of the solar system were to suddenly disappear?
-Without the Sun's gravity, Earth would move in a straight line, with an ever-larger imaginary circle as it travels farther from the point where the Sun used to be.
How does the calculation of angular momentum change if an object's path is not a perfect circle?
-The calculation of angular momentum assumes the object is moving in a circle for simplicity, but the actual path can be approximated by adjusting the circle's size over time to follow the object's trajectory.
Outlines
🌌 Angular Momentum: The Oomph in Circular Motion
This paragraph introduces the concept of angular momentum, which is a measure of the 'oomph' or energy an object has when it is moving in a circular path. It explains that while objects like planets, electrons, and even our solar system may seem to be moving without going anywhere, their motion can be quantified by angular momentum. The paragraph provides a theoretical explanation of how to calculate angular momentum by choosing a point, determining the speed of the object along the circle, and then multiplying this by the circle's size and the object's mass. An example is given with a bicycle wheel to illustrate the calculation. The paragraph also touches on the conservation of angular momentum, stating that the total angular momentum of a system remains constant over time unless external forces are applied. It concludes by emphasizing the constancy of angular momentum even if the forces that created the motion were to disappear, as illustrated by the hypothetical scenario of the sun and the solar system vanishing, leaving Earth with the same angular momentum around the point where the sun used to be.
Mindmap
Keywords
💡Physics
💡Angular Momentum
💡Conservation
💡Orbit
💡Momentum
💡Gravitational Center
💡Mass
💡Velocity
💡Electromagnetic Interaction
💡Law of Physics
💡Imaginary Circle
Highlights
Physics is fundamentally a description of motion in the universe, including objects that appear to move without progressing.
Angular momentum is a concept that quantifies the 'oomph' of objects moving in circular paths.
Angular momentum is calculated by multiplying an object's speed along a circle, the circle's radius, and the object's mass.
A bicycle wheel example illustrates the calculation of angular momentum with specific values.
The total angular momentum of a system remains constant over time unless external forces intervene.
Earth's angular momentum is calculated based on its orbit around the sun, with a constant value over its yearly orbit.
Even if the sun were to disappear, Earth would retain its angular momentum due to the conservation law.
The conservation of angular momentum is demonstrated by Earth's velocity and the imaginary circle's size compensating for each other.
Angular momentum is a fundamental law of physics that holds true even in extreme hypothetical scenarios.
The concept of angular momentum is applicable to a variety of objects, from planets to electrons.
The importance of angular momentum lies in its role in the dynamics of electromagnetic and gravitational interactions.
Angular momentum is a measure that remains unchanged regardless of the object's path or the circle's size variations.
The law of conservation of angular momentum is a testament to the robustness of physical laws, even under disruption.
The transcript provides a clear explanation of a complex physical concept using relatable examples.
Angular momentum is a key factor in understanding the motion of celestial bodies and subatomic particles.
The transcript emphasizes the universality of physical laws, such as angular momentum, across different scales of motion.
The conservation of angular momentum is a principle that applies to both macroscopic and microscopic phenomena.
The transcript explains the theoretical and practical implications of angular momentum in a straightforward manner.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: