Rotational Inertia

Bozeman Science
9 Apr 201505:38
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of rotational inertia, a fundamental principle in physics that governs the resistance to changes in rotational motion. It uses the example of a tractor's flywheel to illustrate how the mass distribution and radius from the center of rotation affect an object's rotational inertia. The script further explains the relationship between angular momentum, rotational inertia, and angular velocity, emphasizing their importance in energy storage and industrial applications. It also touches on the historical invention of the variable flywheel by Leonardo da Vinci and its implications for maintaining constant velocity. The analogy of celestial bodies, like satellites and planets, is used to demonstrate how changes in rotational inertia can impact orbital periods, highlighting the universal application of these principles.

Takeaways
  • 🌐 The concept of rotational inertia is crucial in understanding how objects store and release energy during rotation.
  • βš™οΈ Rotational inertia depends on the mass distribution of an object and its distance from the axis of rotation.
  • πŸ”„ Angular momentum is composed of both rotational inertia and angular velocity, which is the speed at which an object rotates.
  • 🚜 In industrial applications, flywheels are used to store energy, especially during engine idling or startup.
  • πŸ“ The formula for calculating rotational inertia is I = (1/2)mr^2 for a uniform disk, where m is the mass and r is the radius.
  • 🎢 When stopping a rotating object, its rotational inertia and spinning velocity determine the difficulty in stopping it.
  • πŸ“Š Changing the mass distribution on a rotating object, such as moving mass to the outer edge, can alter its rotational inertia and thus its angular momentum.
  • πŸ”„ Leonardo da Vinci's variable inverter flywheel concept utilized the principle of changing rotational inertia to maintain a constant crank velocity.
  • 🌍 Orbital bodies like satellites, the moon, and planets exhibit rotational inertia and angular momentum in their motion around other celestial bodies.
  • πŸš€ Conservation of angular momentum in celestial mechanics means that changes in an object's position can lead to changes in its orbital velocity.
  • πŸ”’ AP Physics courses require students to understand and apply formulas for calculating rotational inertia for various objects.
Q & A

  • What is rotational inertia?

    -Rotational inertia is a measure of the resistance of an object to rotational motion when a torque is applied. It depends on the mass of the object and the distribution of that mass relative to the axis of rotation.

  • How is angular momentum related to rotational inertia and angular velocity?

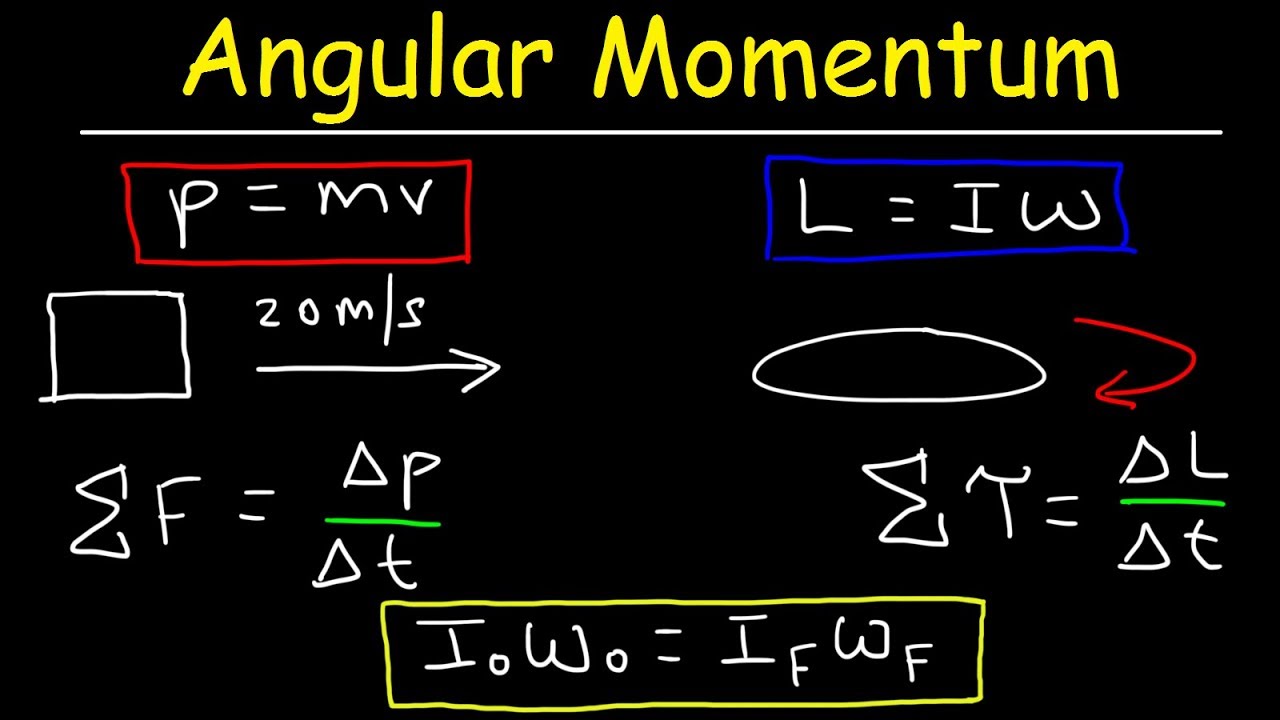
    -Angular momentum (L) is the product of rotational inertia (I) and angular velocity (omega). It is a measure of the rotational motion of an object and is conserved in the absence of external torques.

  • What is the formula for calculating rotational inertia for an object with mass distributed uniformly around a central point?

    -The formula for calculating rotational inertia (I) when the mass is uniformly distributed is I = 1/2 mr^2, where m is the mass and r is the radius from the center of rotation.

  • How does changing the distribution of mass in an object affect its rotational inertia?

    -Changing the distribution of mass towards the outer edges of an object increases its rotational inertia. For instance, if all the mass is on the outside, the formula becomes I = mr^2, without the 1/2 factor.

  • Why are flywheels designed with mass distributed on the outside?

    -Flywheels are designed with mass on the outside to maximize their rotational inertia, which allows them to store more energy and maintain a constant velocity, providing a smooth and steady operation.

  • What is the significance of Leonardo da Vinci's variable inverter flywheel?

    -Leonardo da Vinci's variable inverter flywheel was innovative because it adjusted the rotational inertia by moving spheres towards the outer edge during rotation, allowing for a constant velocity crank operation and efficient energy storage and release.

  • How does the conservation of angular momentum apply to celestial bodies like planets and satellites?

    -The conservation of angular momentum applies to celestial bodies in their orbits. The angular momentum is determined by the mass, radius, and velocity of the orbiting body. If the mass or radius changes while conserving angular momentum, the velocity and hence the orbital period will also change.

  • What would happen if the Earth were moved to a different position in its orbit while conserving angular momentum?

    -If the Earth were moved to a different position with conserved angular momentum, its orbital velocity would increase because it would be closer to the Sun, resulting in a shorter year.

  • How does the shape of an object affect its rotational inertia?

    -The shape of an object affects its rotational inertia because it determines how the mass is distributed in relation to the axis of rotation. Different shapes will have different moments of inertia, which are used in the formulas to calculate rotational inertia.

  • What is the relationship between linear momentum and angular momentum?

    -Linear momentum (p) is the product of mass (m) and linear velocity (v), while angular momentum (L) is the product of rotational inertia (I) and angular velocity (omega). Both are forms of momentum, but linear momentum pertains to motion in a straight line, whereas angular momentum pertains to rotational motion.

  • How does the rotational inertia of a record affect its ease of stopping?

    -A record with a higher rotational inertia, due to its mass and radius, will be more resistant to changes in its rotational motion and thus harder to stop.

Outlines
00:00
πŸ”„ Introduction to Rotational Inertia and Angular Momentum

This paragraph introduces the concept of rotational inertia and angular momentum in the context of a rotating object, such as a flywheel on a tractor. It explains that rotational inertia depends on the object's mass distribution relative to the axis of rotation and that it can store energy. The paragraph also discusses the relationship between angular momentum, rotational inertia, and the velocity of spinning objects. It emphasizes the importance of conservation of angular momentum and how changes in the position of mass within a rotating system affect its rotational inertia and velocity. The formula for calculating rotational inertia (I = 1/2 mr^2) is introduced, along with an example calculation for a spinning record.

05:04
πŸ“š Calculating and Understanding Angular Momentum

This paragraph delves deeper into the calculation and understanding of angular momentum for rotating objects. It highlights the dependency of angular momentum on both the rotational inertia and the velocity of the object. The explanation includes the formula for angular momentum (L = Iω) and its components, where ω represents angular velocity and I is the rotational inertia. The paragraph also discusses how changing the mass distribution on a rotating object, such as moving mass to the outer edge of a record, can alter its rotational inertia and consequently its angular momentum. The innovative flywheel design by inventor Leonardo da Vinci is mentioned, which adjusts its rotational inertia by moving spheres outward as it spins, allowing for a constant velocity crank. The concept is further illustrated with examples of celestial bodies in orbit, showing how their angular momentum and orbital periods are related to their mass distribution and distance from the central body.

Mindmap
Keywords
πŸ’‘Rotational Inertia
Rotational inertia is a measure of the resistance of an object to rotational motion when a torque is applied. It depends on the mass of the object and the distribution of the mass relative to the axis of rotation. In the context of the video, the flywheel's large rotational inertia is due to its significant mass distributed far from the rotation point, making it a good energy storage device. The formula for calculating rotational inertia (I) is given as I = 1/2 mr^2 for a uniform disk, where m is the mass and r is the radius from the center to the edge of the object.
πŸ’‘Angular Momentum
Angular momentum is a measure of the rotational motion of an object, defined as the product of the object's moment of inertia (I) and its angular velocity (omega). It is a conserved quantity in the absence of external torques. In the video, the angular momentum of a system is based on the rotational inertia and the velocity of the objects. The conservation of angular momentum is illustrated by how changes in the position of objects (affecting their rotational inertia) lead to changes in their velocity.
πŸ’‘Angular Velocity
Angular velocity is the rate at which an object rotates around a fixed axis, typically measured in radians per second. It is a component of the angular momentum equation and is directly related to how fast an object is spinning. In the video, the angular velocity of the flywheel or any rotating object is a key factor in determining its angular momentum.
πŸ’‘Conservation of Angular Momentum
The principle of conservation of angular momentum states that the total angular momentum of a closed system remains constant if no external torques act on it. This means that if the position of objects within a system changes, leading to a change in their rotational inertia, their angular velocity must adjust to keep the total angular momentum the same. The video uses this concept to explain how changes in the distribution of mass in a system, such as a flywheel, can affect its rotational inertia and consequently its angular momentum.
πŸ’‘Moment of a Particle
The moment of a particle, or simply momentum (p), is the product of the object's mass (m) and its velocity (v) in a straight line. It is a fundamental concept in classical mechanics that describes the motion of an object. In the video, the concept is extended to rotational motion, where the equivalent of momentum is called angular momentum (L), which is the product of rotational inertia (I) and angular velocity (omega).
πŸ’‘Mass Distribution
Mass distribution refers to how the mass of an object is spread out or arranged in relation to its axis of rotation. The distribution of mass significantly affects the rotational inertia of an object. In the video, it is shown that placing more mass further from the center of rotation increases rotational inertia, which in turn increases the object's angular momentum and its ability to store energy.
πŸ’‘Inverter di Vinci
The Inverter di Vinci, as mentioned in the video, is a type of flywheel invented by Leonardo da Vinci that had variable rotational inertia. As the flywheel rotated, spheres would move outward, increasing the mass distribution and thus the rotational inertia. This design allowed for a constant velocity output, as the flywheel could maintain a steady speed even as its mass distribution changed due to the shifting spheres.
πŸ’‘Energy Storage
Energy storage refers to the process of accumulating energy produced at one time so that it can be used at a later time. In the context of the video, flywheels are used as a means of energy storage due to their ability to store rotational energy through their rotational inertia. When the flywheel is spinning, it stores energy that can be released or used when needed.
πŸ’‘Satellites and Orbits
Satellites and orbits are discussed in the video as examples of angular momentum in celestial bodies. A satellite, such as the moon orbiting the Earth, has a large angular momentum due to its vast distance from the Earth and the time it takes to complete an orbit. The concept is used to illustrate how changes in the position of orbiting bodies, while conserving angular momentum, would affect their orbital velocity and period.
πŸ’‘Position and Velocity
In the context of the video, position and velocity are critical components of angular momentum. The position of objects within a system affects their rotational inertia, which in turn influences the system's angular momentum. Velocity is the rate of change of position and is directly related to the angular momentum of rotating objects. Changes in either position or velocity, while conserving angular momentum, will result in compensatory changes in the other to maintain the same total angular momentum.
Highlights

The concept of rotational inertia is introduced, which is a measure of an object's resistance to changes in its rotation.

Rotational inertia depends on the object's mass distribution and its distance from the point of rotation.

The flywheel on a tractor is used as an example to illustrate the concept of storing energy through rotational inertia.

Industrial fly wheels are being used in factories to store energy, highlighting the practical applications of rotational inertia.

Angular momentum is composed of rotational inertia and angular velocity, which is a key principle in understanding rotating systems.

The conservation of angular momentum implies that changes in an object's position will result in changes in its velocity.

The formula for linear momentum (p = m v) is contrasted with the formula for angular momentum (L = I omega), showing the difference between linear and rotational motion.

The rotational inertia of a record is calculated using the formula I = 1/2 m r^2, demonstrating how to apply the concept in a real-world example.

Changing the mass distribution of an object, such as moving the mass to the outer edge of a record, can alter its rotational inertia.

The rotational inertia can be doubled by positioning all mass on the outside of an object, resulting in twice the angular momentum at the same speed.

The historical innovation of the inverter di Vinci's flywheel is discussed, which adjusts its rotational inertia by moving spheres outward as it rotates.

The flywheel's design allows for a constant velocity crank, showcasing the ingenuity of early mechanical engineering.

Rotational inertia is also applicable to celestial bodies, such as satellites orbiting the Earth and the Moon orbiting the Earth.

The angular momentum of the Earth in its orbit around the Sun is discussed, and how changing its position would affect its velocity and the length of a year.

The importance of understanding both the speed and the rotational inertia in calculating the angular momentum of a rotating object is emphasized.

The transcript provides a comprehensive overview of rotational inertia, its calculation, and its applications in both mechanical and celestial systems.

Transcripts

Browse More Related Video

AP Physics 1 Torque and Rotational Motion Review

Rotation Free Response Paragraph Questions (AP Physics 1)

AP Physics 1 review of Torque and Angular momentum | Physics | Khan Academy

College Physics 1: Lecture 25 - Moment of Inertia and Rotational Dynamics

Angular Momentum - Basic Introduction, Torque, Inertia, Conservation of Angular Momentum

Rotational Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsRotational InertiaAngular MomentumEnergy StorageFlywheelsMechanical EnergyAP PhysicsInertia CalculationSpace DynamicsConservation Laws