Increasing/decreasing functions [IB Maths AI SL/HL]
TLDRThe video script is an engaging exploration of calculus concepts, specifically focusing on increasing and decreasing functions. The presenter uses the analogy of walking up and down a hill to explain when a function is increasing or decreasing, correlating it with the concept of the derivative, which represents the gradient or steepness of the function's graph. The script provides a step-by-step guide on how to determine these properties by finding the function's derivative and setting it greater than or less than zero. The presenter also demonstrates the process using a calculator to graph the function and find its maximum and minimum points, which are crucial for identifying intervals of increase and decrease. The summary also hints at the broader applications of derivatives in finding maxima and minima, which can be useful in various real-world scenarios.
Takeaways
- 📈 Understanding increasing and decreasing functions is crucial in calculus as it helps to determine the direction of a function's growth or decline.
- 🔍 The concept of a function 'going up a hill' signifies an increasing function, while 'going down a hill' indicates a decreasing function.
- 🧮 The derivative, denoted as f'(x), represents the gradient or slope of a function and is key to identifying increasing and decreasing functions.
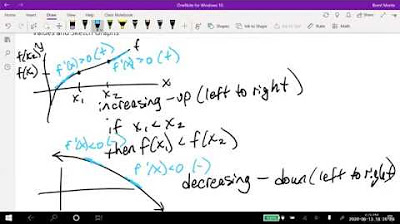
- ➡️ When walking from left to right on a graph, if you're always going 'uphill', the derivative is positive, indicating an increasing function.
- ⬇️ When walking from left to right on a graph, if you're always going 'downhill', the derivative is negative, indicating a decreasing function.
- 📌 At points where the gradient is zero (f'(x) = 0), the function is neither increasing nor decreasing, which could indicate a local maximum or minimum.
- 📊 To find where a function is increasing or decreasing, one can sketch a graph, find the maximum and minimum points, and then determine the intervals between them.
- 🔢 For the given function f(x) = 2x^3 + 3x^2 - 12x - 5, the derivative can be calculated as f'(x) = 6x^2 + 6x - 12, which helps in finding the critical points.
- 🔍 Setting the derivative equal to zero can help find the x-values where the function has a maximum or minimum, which are the points where the gradient is zero.
- 📐 Using a calculator can simplify the process of finding maxima and minima, but it's also possible to solve these problems by hand using algebraic techniques.
- 🚧 The knowledge of derivatives is not only useful for identifying increasing and decreasing functions but also for finding the maximum and minimum values of a function, which has practical applications in various fields.
Q & A
What does the term 'increasing function' mean in the context of calculus?
-An increasing function refers to a function whose value increases as the input (usually represented by 'x') increases when moving from left to right on a graph. It is analogous to walking up a hill, where the gradient or slope is positive.
What does the term 'decreasing function' mean in the context of calculus?
-A decreasing function is one whose value decreases as the input increases when moving from left to right on a graph. It is similar to walking down a hill, where the gradient or slope is negative.
How is the concept of a function increasing or decreasing related to its derivative?
-The derivative of a function at a certain point gives the gradient or slope of the function's tangent line at that point. If the derivative (f prime of x) is positive, the function is increasing; if it is negative, the function is decreasing; and if it is zero, the function has a flat tangent, which could indicate a local maximum or minimum.
What is a 'pro tip' given in the transcript for understanding the concept of increasing and decreasing functions?
-The pro tip is to imagine walking from left to right on a graph. If you are going 'up a hill,' the function is increasing (positive derivative), and if you are going 'down a hill,' the function is decreasing (negative derivative).
Why is it useful to know where a function increases or decreases?
-Knowing where a function increases or decreases can be useful for various applications, such as finding the maximum or minimum values of a function, understanding the behavior of the function, or analyzing its growth rate.
How can one find the intervals where a function is increasing or decreasing?
-One can find these intervals by calculating the derivative of the function and determining where it is positive (increasing) or negative (decreasing). Additionally, finding local maxima and minima can help identify intervals where the function changes from increasing to decreasing or vice versa.
What is the process described in the transcript for finding the intervals of increase and decrease for the function f(x) = 2x^3 + 3x^2 - 12x - 5?
-The process involves finding the derivative of the function, setting it equal to zero to find critical points, and then using a graphing calculator to sketch the function and identify the intervals of increase and decrease based on the sign of the derivative.
How does the concept of a function's maximum and minimum relate to its derivative?
-A function's maximum or minimum occurs where its derivative is zero or undefined. These points are where the function changes from increasing to decreasing (or vice versa), and they can be found by setting the derivative equal to zero and solving for 'x'.
What is the significance of finding the maximum and minimum values of a function?
-Finding the maximum and minimum values of a function is significant because it can provide insights into the behavior of the function, such as its peak effectiveness or productivity, and can be crucial in optimization problems and real-world applications.
How can one find the maximum and minimum values of a function using a graphing calculator?
-One can use the analyze feature of a graphing calculator to find the maximum and minimum values of a function by specifying the left and right bounds of the interval in which the maximum or minimum occurs.
What is the importance of understanding the relationship between a function's graph and its derivative?
-Understanding this relationship is crucial because it allows one to visualize and predict the behavior of the function based on its derivative. It helps in identifying intervals of increase and decrease, locating maxima and minima, and understanding the function's overall trend.
What is the role of the second derivative in analyzing the function's behavior?
-While not explicitly covered in the transcript, the second derivative can provide information about the concavity of the function and can help determine whether a critical point is a maximum, minimum, or inflection point.
Outlines
📈 Understanding Increasing and Decreasing Functions
This paragraph introduces the concept of increasing and decreasing functions in calculus. It explains that by examining the derivative (or f prime), one can determine whether a function is increasing (going uphill) or decreasing (going downhill) as one moves from left to right on a graph. The speaker uses the analogy of walking to visualize the direction of the function's movement. The paragraph also touches on the idea that the derivative represents the slope or steepness of the function, and provides a method to identify increasing functions by checking when the derivative (f prime of x) is greater than zero.
📉 Analyzing the Function's Behavior with a Calculator
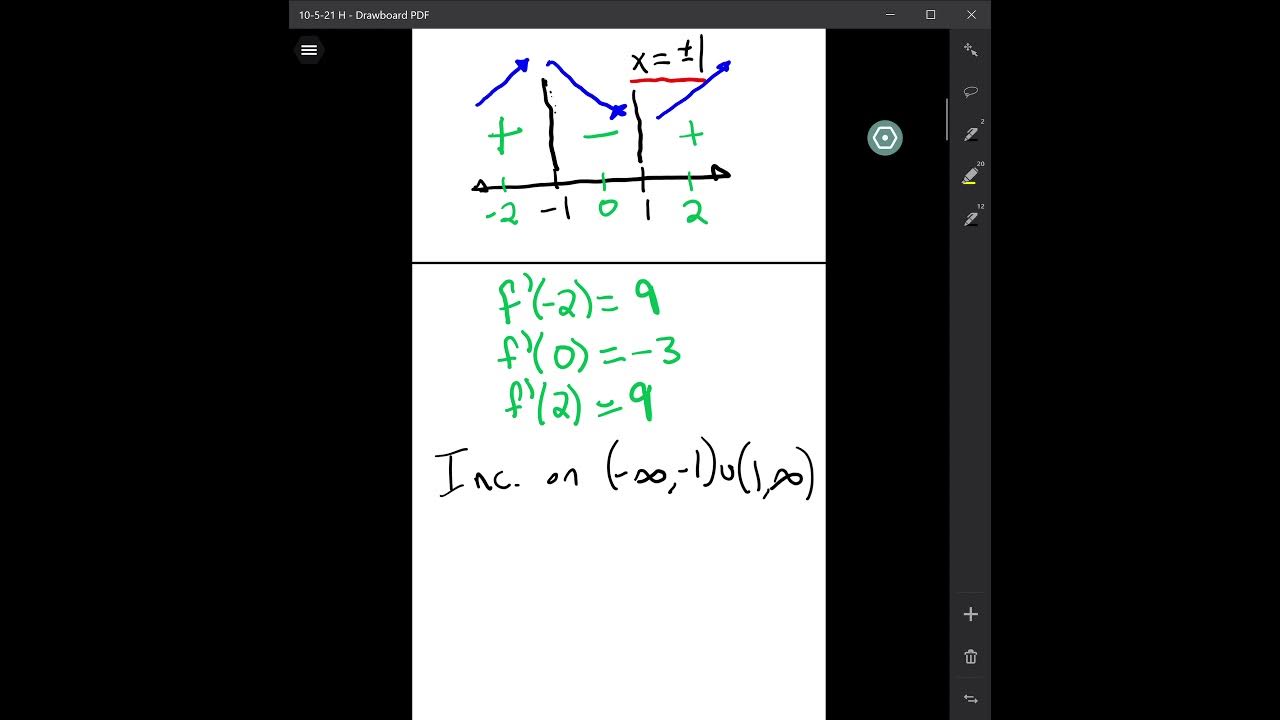
The second paragraph delves into applying the concept of increasing and decreasing functions to a specific example: f(x) = 2x^3 + 3x^2 - 12x - 5. The speaker uses a calculator to graph the function and identify its maximum and minimum points, which are crucial for understanding where the function changes from increasing to decreasing or vice versa. The maximum is found at x = -2, and the minimum at x = 1. The paragraph explains how to determine the intervals where the function is increasing (f prime of x > 0) and decreasing (f prime of x < 0), and emphasizes the importance of these intervals in understanding the function's behavior. It concludes by noting that while a calculator can assist in finding these points, one could also solve for them manually by setting the derivative to zero and solving for x.
Mindmap
Keywords
💡Calculus
💡Derivatives
💡Increasing Function
💡Decreasing Function
💡Gradient
💡Tangent Line
💡Function
💡Graph
💡Maximum and Minimum
💡Set Notation
💡Calculator
Highlights
The calculus course focuses on understanding the concepts of increasing and decreasing functions using derivatives.
Derivatives are used to find gradients of tangent lines and to determine where a function increases or decreases.
An intuitive approach to understanding derivatives is imagining walking from left to right on a graph, where going uphill indicates an increasing function.
The derivative, f prime, represents the gradient of a function and is related to the steepness of the slope.
A positive derivative indicates an increasing function, while a negative derivative indicates a decreasing function.
The concept of 'going uphill' is used to visualize when a function's derivative is positive.
A derivative equal to zero suggests a flat slope, which could indicate a maximum or minimum point.
The function f(x) = 2x^3 + 3x^2 - 12x - 5 is used as an example to demonstrate how to find increasing and decreasing intervals.
Graphical representation and calculators can be used to sketch and analyze the behavior of a function.
The maximum and minimum points of a function are important for understanding where it is not increasing or decreasing.
The x-values at which a function has a maximum or minimum can be found using a calculator or by setting the derivative to zero and solving.
The derivative being greater than zero indicates an increasing function, while less than zero indicates a decreasing function.
Set notation is used to elegantly express the intervals where a function is increasing or decreasing.
Derivatives can be used to find not only the increasing and decreasing intervals but also the maximum and minimum values of a function.
The practical applications of derivatives include determining the maximum growth rate or effectiveness in various fields such as medicine.
The video provides a pro tip on using the concept of walking uphill or downhill to understand the behavior of a function's derivative.
The importance of understanding the concept of derivatives is emphasized for its wide range of applications in calculus.
Transcripts
Browse More Related Video
Math 11 - Section 3.1

AP Calc - Graphing f from f'
Relative Maxima/Minima Examples

Maximum / minimum [IB Maths AI SL/HL]

Business Calculus - Math 1329 - Section 4.4 - Applications of Exponential and Logarithmic Functions

Concavity introduction | Using derivatives to analyze functions | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: