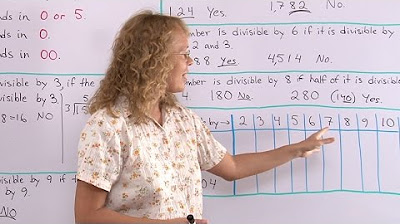An "unsolvable" logic puzzle
TLDRIn this video, Presh Talwalkar presents a mathematical puzzle involving two different one-digit numbers whose product's last digit matches Brian's house number. The challenge is to determine the sum of these two numbers. Through elimination, they deduce that Brian's house number could only be 1 or 9, as these are the only cases with a unique product. Interestingly, both scenarios yield the same sum for the two numbers, which is 10 (1+9 and 3+7). The video cleverly guides viewers on how to solve such problems and highlights the beauty of mathematical reasoning.
Takeaways
- 🔢 Avery is thinking of two different one-digit numbers and challenges others to guess them.
- 🏠 Brian's house number is a clue to the puzzle, as it is the last digit of the product of the two numbers.
- 🤔 Brian works out the problem and realizes the sum of the two numbers based on the clue.
- 📊 A multiplication table is used to enumerate the possible products of two one-digit numbers.
- ❌ Diagonal and identical lower half of the multiplication table are eliminated since they are commutative and not needed.
- 🚫 Brian's house number cannot be 2, 3, 4, 5, 6, 7, 8, or 0 because there are too many possibilities for those numbers.
- 💡 The only numbers with a unique product based on the last digit are 1 and 9, leading to a single solution.
- 🔍 The sum of the two numbers is determined to be 10, regardless of whether Brian's house number is 1 or 9.
- 🎓 The problem is adapted from a 2015 Singapore Olympia Challenge for primary five students.
- 🎶 The video features music and encourages viewers to pause and try solving the problem on their own.
- 🌐 The video is part of a YouTube community that solves problems one video at a time.
Q & A
What is the nature of the numbers Avery is thinking of?
-Avery is thinking of two different one-digit numbers.
What clue does Avery provide to Bryant about the numbers?
-The last digit of the product of the two numbers is the same as Bryant's house number.
How does Brian deduce the sum of the two numbers?
-Brian deduces the sum by eliminating possibilities based on the last digit of the product of the numbers and the fact that there's only one unique product for each possible house number.
Why couldn't Brian's house number be two?
-Because there are many products with a last digit of two, leading to different sums, so Brian couldn't have determined the unique sum of the two numbers.
What is the significance of the multiplication table in solving the problem?
-The multiplication table is used to enumerate all possible products of two one-digit numbers to find the one that matches the clue given by Avery.
Why are the numbers on the diagonal of the multiplication table not considered?
-The numbers on the diagonal of the multiplication table are not considered because they represent the square of a number, which is not a product of two different one-digit numbers.
What is the only product that has a last digit of zero?
-The only product with a last digit of zero is 10, which is the product of 1 and 10, but since 10 is not a one-digit number, it is not considered.
What is the sum of the two numbers if Brian's house number is one?
-If Brian's house number is one, the sum of the two numbers is 10, as 1 times 9 equals 9.
What is the sum of the two numbers if Brian's house number is nine?
-If Brian's house number is nine, the sum of the two numbers is also 10, as 3 times 7 equals 21.
What is the conclusion about the sum of the two numbers regardless of Brian's house number?
-The sum of the two numbers is definitively ten, regardless of whether Brian's house number is one or nine.
What type of mathematical property is used to simplify the multiplication table in the script?
-The commutative property of multiplication is used to simplify the table, which states that the order of factors does not change the product.
What is the source of the problem presented in the script?
-The problem is adapted from a 2015 Singapore Olympia Challenge for primary five students.
Outlines
🧐 Riddle of the One-Digit Numbers
The video introduces a riddle where Avery thinks of two different one-digit numbers and challenges others to guess them. The clue given is that the last digit of their product matches Brian's house number. The video then invites viewers to solve the problem and proceeds to enumerate possible products of one-digit numbers, creating a multiplication table and eliminating products based on the clue provided. The focus is on finding a unique pair of numbers whose product's last digit could help identify the sum of the numbers. Through elimination, it's concluded that Brian's house number could be either 1 or 9, leading to the solution that the sum of the two numbers is 10.
Mindmap
Keywords
💡One-digit numbers
💡Product
💡Last digit
💡House number
💡Sum
💡Multiplication table
💡Commutative property
💡Enumerate
💡Eliminate possibilities
💡Singapore Olympiad Challenge
💡Mind Your Decisions
Highlights
Avery and Brian engage in a conversation where Avery thinks of two different one-digit numbers.
Avery provides a clue that the last digit of the product of the two numbers is the same as Brian's house number.
The problem is adapted from a 2015 Singapore Olympia Challenge for primary five students.
Enumeration of possible products of two one-digit numbers through a multiplication table is suggested.
The multiplication table is cleaned up by eliminating the diagonal and considering only one-digit numbers.
Brian's house number is a key to solving the puzzle, but it is not known to the audience.
The possibility of Brian's house number being 2, 3, 4, 5, 6, 7, 8, or 0 is eliminated due to multiple possible products.
Only one case remains for the house number being 9, which narrows down the possibilities.
Another possibility is that Brian's house number is 1, which also leads to a single case.
Interestingly, both cases where the house number is 9 or 1 result in the same sum for the two numbers.
The sum of the two numbers is definitively identified as ten, regardless of Brian's house number.
The puzzle demonstrates the use of logical elimination and pattern recognition to solve a problem.
The video encourages viewers to pause and attempt the problem before revealing the solution.
The problem-solving approach involves creating a multiplication table and evaluating each product.
The video explains the commutative property of multiplication in the context of the puzzle.
The process of elimination is used to identify the sum of the two numbers by considering the last digit of their product.
The video concludes by emphasizing the importance of logical thinking and problem-solving skills.
The solution to the puzzle is presented in an engaging and educational manner.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: