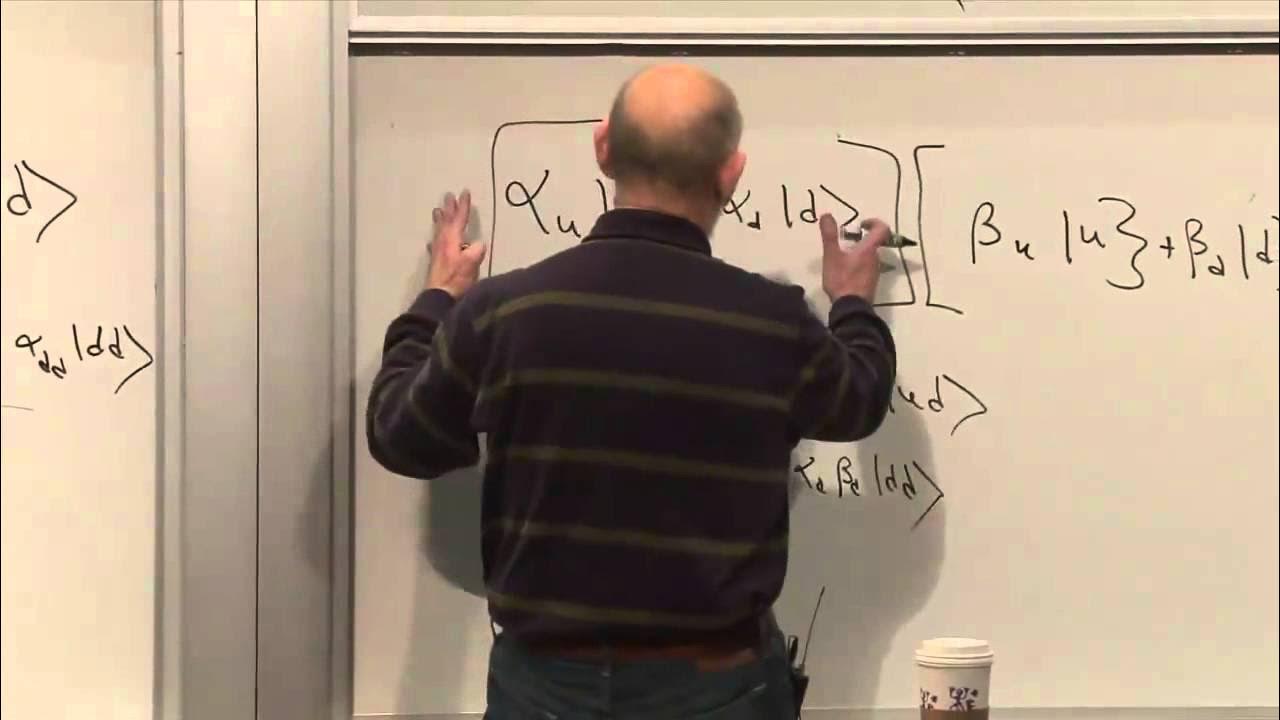Statistical Mechanics Lecture 4
TLDRThe video script is a detailed lecture on statistical mechanics, focusing on the Boltzmann distribution and its application to an ideal gas. The lecturer begins by reviewing the principles of calculating probabilities for different states of a system, introducing the concept of occupation numbers. They derive the probability distribution and entropy of the system, explaining how to maximize entropy while adhering to constraints. The method of Lagrange multipliers is used to find the most likely set of occupation numbers, leading to the introduction of the partition function, a key concept in statistical mechanics. The script then delves into calculating the average energy, entropy, and temperature of the system using the partition function. The lecturer also discusses how to handle systems with different conserved quantities and control parameters. An example of an ideal gas in a gravitational field is used to illustrate the calculation of the partition function and its implications on the system's energy and entropy. The lecture concludes with a discussion on the importance of fluctuations in energy and the historical context of statistical mechanics, hinting at future topics to be covered in subsequent sessions.
Takeaways
- 📚 The concept of statistical mechanics is introduced, focusing on the Boltzmann distribution and its application to an ideal gas example.
- ⚖️ The probability distribution over the states of a system is derived from the principle of maximizing entropy, subject to energy constraints.
- 🎯 The method of Lagrange multipliers is used to find the most probable set of occupation numbers, which leads to the derivation of the Boltzmann distribution.
- 🔄 The partition function (Z) is central to statistical mechanics, as it encodes the system's average energy and allows for the calculation of entropy and temperature.
- 🌡️ The relationship between the Lagrange multiplier β (beta) and temperature is established, revealing that β is the inverse of temperature (β = 1/kT, where k is the Boltzmann constant).
- 📉 The average energy of a system can be determined from the partition function by differentiating the natural logarithm of Z with respect to β.
- 🤔 The script touches on the concept of entropy and its calculation in terms of the partition function, emphasizing the importance of entropy in statistical mechanics.
- 🚀 The ideal gas is used as an example to illustrate the calculation of the partition function, highlighting the simplifications that occur when interactions between particles are negligible.
- 🧮 An integral over the phase space of the system is performed to calculate the partition function for an ideal gas, considering both position and momentum coordinates.
- ⛰️ The script briefly mentions the impact of a gravitational field on the partition function, indicating how potential energy considerations can modify the distribution.
- ⚛️ Fluctuations in energy and their relation to specific heat are hinted at as a topic for future discussion, emphasizing the importance of understanding statistical fluctuations in physical systems.
Q & A
What is the Boltzmann distribution?
-The Boltzmann distribution is a statistical distribution that describes the probability of a system being in a certain state at a given temperature. It is used in statistical mechanics to predict the distribution of energy in a system of particles.
How is the probability of a state in a system calculated?
-The probability of a state in a system is calculated using the Boltzmann distribution formula, which involves the energy of the state and a partition function. The probability is proportional to the exponential of the negative energy of the state divided by the product of the temperature and the Boltzmann constant.
What is a partition function?
-A partition function is a mathematical function that encodes the statistical properties of a system in thermodynamic equilibrium. It is used to calculate the average energy, entropy, and other thermodynamic quantities of a system.
What is the significance of the Lagrange multipliers in the context of statistical mechanics?
-In statistical mechanics, Lagrange multipliers are used to find the maximum entropy distribution subject to constraints, such as the total energy of the system and the normalization condition that the sum of probabilities must equal one.
How is the average energy of a system calculated?
-The average energy of a system is calculated by differentiating the logarithm of the partition function with respect to the inverse temperature (beta). This gives a relationship between the average energy and the temperature of the system.
What is the relationship between beta and temperature?
-Beta is the inverse of the temperature. Specifically, beta equals 1 over the product of the temperature and the Boltzmann constant. This relationship is derived from the definition of temperature as the rate of change of energy with respect to entropy.
How is entropy calculated in the context of statistical mechanics?
-Entropy in statistical mechanics is calculated using the formula that involves the sum over all states of the system of the probability of each state multiplied by the logarithm of that probability. It can also be expressed in terms of the partition function as the sum of beta times the average energy plus the logarithm of the partition function.
What is the significance of the partition function for an ideal gas?
-The partition function for an ideal gas provides a way to calculate the average energy, entropy, and other thermodynamic properties of the gas. It is particularly important because it allows for the calculation of these properties as a function of temperature and volume.
How does the presence of a gravitational field affect the partition function of a gas?
-In the presence of a gravitational field, an additional potential energy term is included in the calculation of the partition function. This term accounts for the work done against gravity and modifies the energy levels of the gas, leading to changes in the distribution of energy among the particles.
What is the role of the method of Lagrange multipliers in finding the most probable distribution of energy?
-The method of Lagrange multipliers is used to find the distribution of energy (occupation numbers) that maximizes entropy while adhering to constraints, such as the total energy of the system. It is a powerful tool for solving optimization problems in statistical mechanics.
How does the concept of fluctuations in energy relate to specific heat?
-Fluctuations in energy are related to specific heat through a formula that connects the variance of the energy distribution to the specific heat capacity of the system. This relationship is important for understanding how energy is distributed and how it changes with temperature in a system.
Outlines
😀 Introduction to Statistical Mechanics and Boltzmann Distribution
The speaker begins by expressing their intention to delve into the core of statistical mechanics, focusing on the Boltzmann distribution. They aim to illustrate this concept with an example of an ideal gas. A quick review of previously discussed principles for calculating probabilities is also mentioned, emphasizing the importance of understanding occupation numbers and their role in defining the probability distribution of a system's states. The concept of entropy as a function of these probabilities is introduced, and its calculation from a constrained maximization problem is outlined.
📚 Constraints and the Method of LaGrange Multipliers
The paragraph explains the use of constraints in statistical mechanics and introduces the method of LaGrange multipliers for finding the minimum of a function subject to these constraints. The speaker details the process of adding constraint equations multiplied by Lagrange multipliers to the function to be minimized. Two constraints are identified: the normalization of probabilities and the fixed average energy per subsystem. The role of Lagrange multipliers, denoted as alpha and beta, is discussed in the context of these constraints.
🔍 Minimization and Differentiation for Finding Minimum
The focus shifts to the process of minimizing the function F, which includes the probabilities and constraints. The speaker outlines the steps for differentiation with respect to the probabilities and setting the derivatives equal to zero to find the minimum. The differentiation process simplifies by ignoring constants and focusing on terms involving the probabilities. The resulting equation is shown to provide insight into the probabilities of the states.
🎚️ Probability Distribution and the Significance of Beta
The speaker derives the probability distribution for the states of a system, emphasizing the role of the Lagrange multipliers, particularly beta, in determining the average energy. The relationship between beta and the exponential function of the energy states is explored, revealing that beta is inversely related to temperature. The concept of the partition function Z is introduced, which is a function of beta and is crucial for calculating probabilities.
🔗 Partition Function and Average Energy
The paragraph discusses the partition function's role in determining the average energy of a system. The speaker differentiates the partition function with respect to beta to find a formula that relates the average energy to the partition function. The significance of the partition function in statistical mechanics is highlighted, as it encapsulates all the relevant information about the system.
🔁 Differentiating the Partition Function for Energy and Entropy
The speaker explores the process of differentiating the partition function to find expressions for energy and entropy. They derive a formula for the average energy per box and relate it to the derivative of the logarithm of the partition function with respect to beta. The connection between the partition function and the system's energy as a function of temperature is established.
🌡️ Establishing the Connection Between Beta and Temperature
The paragraph focuses on establishing the relationship between beta and temperature. The speaker uses the definition of temperature as the change in energy with respect to entropy to derive that the temperature is the inverse of beta. This connection is crucial for understanding the physical significance of beta and its role in statistical mechanics.
📉 Entropy Calculation and its Relation to Partition Function
The speaker calculates the entropy of the system using the partition function. They derive an expression for entropy in terms of the partition function and show how it can be used to calculate the entropy and, subsequently, the temperature of the system. The importance of the logarithm of the partition function in statistical mechanics is emphasized.
🧮 Partition Function Calculation for an Ideal Gas
The speaker provides an example of calculating the partition function for an ideal gas, which is a collection of non-interacting point molecules inside a box. They discuss the energy states of the system and how to calculate the partition function using integrals over the positions and momenta of the molecules. The process involves summing over all possible states and integrating over the momentum space.
🚀 Application to a Gas in a Gravitational Field
The speaker explores the implications of considering a gas in a gravitational field, which introduces a potential energy term into the calculations. They discuss how the partition function would be affected and how the energy per particle would include a contribution from the potential energy. The speaker suggests that the problem can be simplified by considering the room to be infinitely high, effectively modeling the atmosphere between the Earth's surface and infinity.
🔍 Fluctuations in Energy and Specific Heat
The speaker concludes by mentioning the concept of energy fluctuations and their relation to specific heat. They suggest that fluctuations were not part of the original thermodynamic theory but were incorporated into statistical mechanics by scientists like Einstein and Gibbs. The speaker hints at deriving a beautiful formula that relates energy fluctuations to specific heat in a future session.
Mindmap
Keywords
💡Statistical Mechanics
💡Boltzmann Distribution
💡Entropy
💡Partition Function
💡Ideal Gas
💡Lagrange Multipliers
💡Thermodynamic Equilibrium
💡Temperature
💡Energy Levels
💡Fluctuations
💡Gibbs Paradox
Highlights
Introduction to the heart of statistical mechanics focusing on the Boltzmann distribution and its significance in understanding the probabilities of states in a system.
Review of the basic principles for calculating probabilities, emphasizing the importance of occupation numbers and their role in defining the probability distribution.
Explanation of entropy as a function of the probabilities of states and its relation to maximizing entropy under constraints.
Introduction of the method of LaGrange multipliers for finding the minimum of a function subject to constraints, a powerful tool in statistical mechanics.
Derivation of the relationship between the probabilities of states and the energy levels, leading to the identification of the partition function.
Discussion on the physical significance of the Lagrange multipliers, particularly the inverse relationship between beta and temperature.
Calculation of the average energy per box in a system using the partition function and its relation to the derivative of the logarithm of the partition function with respect to beta.
Insight into the role of beta as a tuning parameter for the average energy in a system and its connection to the temperature.
Derivation of the entropy formula in terms of the partition function, showcasing its importance in statistical mechanics.
Explanation of the concept of temperature in relation to the rate of change of energy with respect to entropy, providing a clear definition of temperature in the context of statistical mechanics.
Application of the principles to the example of an ideal gas, demonstrating how to calculate the partition function for a system of non-interacting particles.
Integration over the state space of an ideal gas to find the partition function, including both position and momentum components.
Use of the Gaussian integral to simplify the calculation of the partition function for an ideal gas, leading to a closed-form expression.
Derivation of the total energy of a system of ideal gas particles using the partition function and its relation to the temperature.
Discussion on the implications of including a potential energy term in the calculation of the partition function, particularly in the context of a gravitational field.
Calculation of the entropy and entropy per particle for an ideal gas using the partition function as a practical exercise.
Introduction to the concept of fluctuations in energy and their relation to specific heat, highlighting the importance of studying these phenomena in statistical mechanics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: