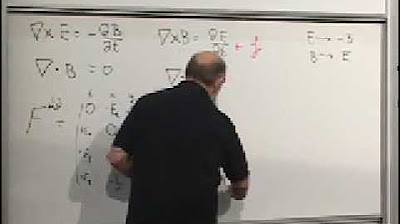Special Relativity | Lecture 7
TLDRThe video script is a detailed lecture on the principles of electromagnetism, focusing on the concept of gauge invariance. The lecturer explains the importance of the action principle in physics, emphasizing that physical phenomena are best described by an action that leads to equations of motion through the Euler-Lagrange equations. The principle of locality is discussed, highlighting that physical interactions are immediate to neighboring points in space and time. The lecturer also delves into Lorenz invariance, the idea that physics remains the same across all reference frames, and introduces the concept of gauge invariance. This involves the vector potential in electromagnetic fields, which can be altered without affecting the physical outcomes, such as the motion of particles. The script is rich with mathematical insights, including the role of four-vectors and tensors in special relativity, and the use of these mathematical tools to express physical laws in a concise and frame-independent manner. The lecturer also clarifies misconceptions about the physical implications of quantum entanglement, stressing that it does not allow for instantaneous signaling or action at a distance. The summary underscores the beauty and simplicity of gauge theories, which are prevalent in fundamental physics, despite the mystery of why nature favors such theories.
Takeaways
- 📚 The lecturer emphasizes the importance of completing a full set of ten lectures, indicating a commitment to ensuring comprehensive course coverage, despite having to miss one week due to a lecture commitment in Belgium.
- 🔍 The speaker acknowledges the complexity of the mathematical content, recognizing that not all students may follow every detail but appreciates their effort to engage with the material.
- ✅ The teaching policy is described as persistent, with the intent to teach until students fully understand, reflecting a dedication to ensuring conceptual clarity even with challenging subjects.
- 🌐 The lecturer discusses the universality of the action principle in physics, suggesting that all phenomena can be described by such a principle, which is crucial for deriving conservation laws.
- 📐 The principle of locality is highlighted, stating that physical interactions are limited to immediate surroundings, which is a fundamental concept in formulating physical theories.
- 🔗 The lecturer refutes misconceptions about quantum entanglement, clarifying that it does not imply non-locality or the instantaneous effect at a distance, but rather a correlation between quantum states.
- 📈 The concept of Lorenz (or Lorentz) invariance is introduced, which requires that the equations of motion remain the same across all reference frames, a cornerstone for the development of the theory of relativity.
- 🔧 The lecture introduces the idea of gauge invariance, a specific type of invariance that allows for changes in the vector potential that do not affect the physical observables, such as electric and magnetic fields.
- 🧲 The vector potential is shown to be a crucial component in formulating the action for a particle in an electromagnetic field, despite not appearing directly in the final equations of motion.
- 🔬 The mathematical structure of the electromagnetic field tensor (Fmunu) is derived, which is essential for understanding how electric and magnetic fields transform under different reference frames.
- ⚙️ The utility of gauge transformations is discussed, noting that while they do not change the physical outcomes, they can simplify calculations and provide insights into the underlying symmetries of physical theories.
Q & A
Why does the lecturer mention that he will not be present next week?
-The lecturer has to travel to Belgium to give a lecture, which is why he will be absent from the course next week.
What is the significance of the 'full set of ten lectures' mentioned by the lecturer?
-The lecturer emphasizes the importance of completing the full set of ten lectures to ensure the course material is fully covered and students receive a comprehensive understanding of the subject.
Why does the lecturer express his teaching policy as 'teach until you cry'?
-This phrase illustrates the lecturer's commitment to ensuring students understand the material thoroughly, even if it requires going over complex concepts multiple times.
What is the role of mathematics in expressing the laws of nature according to the lecturer?
-Mathematics is essential for quantifying the exact and precise laws of nature, as it provides a language for expressing these laws in a clear and systematic way.
What is the 'official rule' regarding the use of lower and upper indices in the context of the lecture?
-The official rule is that when a lower index and an upper index are the same letter, it implies a summation over that index, which is a convention to simplify notation and calculations.
Why does the lecturer discuss the concept of 'locality' in physics?
-Locality is a fundamental principle that states the direct effect of an action is on nearby objects, which is crucial for ensuring the equations of motion are consistent with our understanding of cause and effect in physics.
What is the importance of Lorenz invariance in the context of the lecture?
-Lorenz invariance ensures that the equations of motion are the same in all reference frames, which is a fundamental requirement for a theory to be considered physically valid.
What does the lecturer mean by 'gauge invariance'?
-Gauge invariance refers to the property of a physical system where certain changes, specifically those involving the addition of a gradient of a scalar function to the vector potential, do not affect the physical observables of the system.
Why is the vector potential introduced in the discussion of electromagnetism?
-The vector potential is introduced as an auxiliary field that allows for the formulation of an action principle for the motion of a charged particle in an electromagnetic field, even though its specific value is not physically measurable due to gauge invariance.
What is the significance of the lecturer's statement about the 'theoretical minimum'?
-The 'theoretical minimum' refers to the essential core concepts and principles that one must understand to progress to more advanced topics in physics, which the lecturer aims to convey through the course.
Why does the lecturer mention the possibility of a young person discovering a simplicity in the laws of physics?
-The lecturer suggests that while current theories may appear complex, there may be a simpler, yet undiscovered, formulation of these laws that could be understood in the future, highlighting the evolving nature of scientific understanding.
Outlines
😀 Introduction and Lecture Continuity
The speaker begins by informing the audience that they will be absent next week due to a lecture commitment in Belgium. They assure the attendees that they will complete the full set of ten lectures, despite the temporary absence. The speaker admits to losing track of the lecture sequence but commits to covering all topics. They also express a desire for someone to help digitize their notes by scanning and uploading them to the website, as their own scanner is slow.
🔢 Mathematical Complexity in Physics
The speaker acknowledges the challenging and complex mathematics covered in the lectures, appreciating the audience's effort to follow along. They reiterate their teaching policy of thoroughness, aiming to cover the theoretical minimum necessary for understanding the subject. The speaker discusses the importance of mathematics in expressing the laws of nature, suggesting that while it may seem arcane, it is a fundamental part of quantifying natural laws. They also express hope that someone might simplify these laws in the future.
📏 Coordinates and Indices in Physics
The speaker delves into the technical aspects of coordinates and indices, explaining the arbitrary nature of defining up and down or left and right. They discuss the use of upstairs (contravariant) and downstairs (covariant) indices in labeling coordinates and their differences, particularly in the context of time components. The speaker also explains the efficiency of using these indices in writing simpler expressions and the rules for summing over indices.
🔗 Invariance and Conservation Laws
The speaker emphasizes the importance of describing physical phenomena through an action principle, which underpins the derivation of conservation laws in physics. They assert that without basing equations on an action principle, fundamental conservation laws like energy and momentum conservation cannot be guaranteed. The speaker also touches on the principle of locality, stating that the action should only depend on immediate surroundings in space and time.
🪢 Entanglement and Non-Locality
The speaker clarifies the concept of entanglement in quantum physics, dispelling misconceptions about non-locality. They explain that entanglement does not allow for instant effects at a distance; rather, it involves correlations between quantum states. The speaker stresses the importance of locality in physical theories and the need for the physics to be Lorenz invariant across different reference frames.
🧲 Electromagnetic Fields and Action Principles
The speaker introduces the concept of a four-vector potential necessary for formulating the action principle for a charged particle in an electromagnetic field. They explain that while the Lorentz force law can be written without a vector potential, an action principle that leads to the equations of motion for such a particle requires it. The speaker outlines the components of the action for a particle in an electromagnetic field and how it is derived from the vector potential.
📐 Lagrangian Dynamics
The speaker discusses the process of deriving the Lagrangian for a particle in an electromagnetic field. They explain the mathematical steps involved in differentiating the Lagrangian with respect to velocity and position, resulting in the equations of motion. The speaker emphasizes the tedious but straightforward nature of these mechanical rules in physics.
🤔 The Role of Vector Potential in Physics
The speaker explores the concept of gauge invariance, a principle stating that the physics remains unchanged when the vector potential is altered by the gradient of a scalar function. They demonstrate that such a change, known as a gauge transformation, does not affect the motion of a particle, as it only impacts the action through the endpoints of a trajectory. The speaker also discusses the utility of gauge transformations in simplifying problems and illustrating different properties of a theory.
📡 Measuring Physical Quantities
The speaker concludes by addressing the question of what can be measured in the context of gauge invariance. They assert that while the vector potential itself cannot be measured due to its inherent ambiguity, gauge-invariant quantities such as electric and magnetic fields can be. The speaker emphasizes that the beauty and simplicity of gauge theories are pervasive in physics, even though the reason for nature's preference for these theories is not fully understood.
Mindmap
Keywords
💡Lorentz Invariance
💡Action Principle
💡Vector Potential
💡Gauge Invariance
💡Electromagnetic Field Tensor
💡Principle of Locality
💡Euler-Lagrange Equations
💡Four-Vector
💡Proper Time
💡Lagrangian
💡Conservation Laws
Highlights
The lecturer announces that they will be absent next week due to a lecture commitment in Belgium, but assures the audience that the full set of ten lectures will be delivered.
The importance of mathematical expression in physics is emphasized, as it is seen as a fundamental language that nature's laws are quantified in.
The concept of the four-vector potential is introduced as necessary for formulating the action principle for a charged particle in an electromagnetic field.
The lecturer discusses the principle of locality in physics, which states that physical effects are immediate only to the immediate vicinity of their cause.
The principle of Lorenz invariance is explained, which requires that the equations of motion should be the same in every reference frame.
Gauge invariance is introduced as a fundamental principle in physics, where certain changes in the vector potential do not affect the physics of a system.
The electromagnetic field tensor (F mu nu) is shown to be invariant under gauge transformations, meaning the physics remains unchanged despite changes in the vector potential.
The role of the vector potential in deriving the Lorentz force law is clarified, despite the vector potential itself not being directly measurable.
The distinction between covariant and contravariant vectors is explained, with an emphasis on how they transform under Lorentz transformations.
The lecturer provides a detailed derivation of the equations of motion for a particle in an electromagnetic field using the action principle.
The principle of least action is discussed in the context of finding the trajectory of a particle that minimizes the action, given fixed endpoints.
The concept of the four-velocity and its role in describing the motion of particles in the presence of electromagnetic fields is explored.
The Maxwell tensor components are related to the electric and magnetic fields, providing a link between the field tensor and observable physical quantities.
The utility of gauge transformations in simplifying problems and illustrating different properties of a physical theory is highlighted.
The invariability of physical laws under gauge transformations is emphasized, noting that while the vector potential can change, the physical outcomes remain the same.
The lecturer assures that despite the complexities introduced by gauge invariance, the final physical predictions of the theory do not change, ensuring the theory's consistency.
The philosophical and physical implications of gauge invariance are discussed, noting its pervasive role in fundamental physics theories.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: